초기하 분포

에 의해 벤자민 앤더슨 8월 6, 2023 개연성 댓글 0개

이 기사에서는 초기하 분포가 무엇인지, 그리고 이러한 분포 유형을 사용하여 확률을 계산하는 방법을 설명합니다. 초기하 분포 공식과 그 특성은 물론 초기하 분포의 확률을 계산하는 계산기도 온라인에서 찾을 수 있습니다.

초기하 분포란 무엇입니까?

초기하 분포는 모집단에서 n개의 요소를 대체하지 않고 무작위 추출에서 성공한 사례 수를 설명하는 확률 분포입니다.

즉, 초기하 분포는 모집단에서 n개의 요소를 대체하지 않고 추출할 때 x개의 성공을 얻을 확률을 계산하는 데 사용됩니다.

초기하 분포에는 세 가지 매개변수가 있습니다.

N : 모집단의 요소 수입니다(N = 0, 1, 2,…).
K : 최대 성공 사례 수입니다(K = 0, 1, 2,…,N). 초기하 분포에서는 요소가 “성공” 또는 “실패”로만 간주될 수 있으므로 NK 는 최대 실패 사례 수입니다.
n : 수행된 비대체 가져오기 횟수입니다.

$X \sim HG(N,K,n)$

예를 들어, 매개변수 N=8, K=5 및 n=3을 갖는 초기하 분포를 갖는 이산 확률 변수 X는 다음과 같이 정의됩니다.

$X \sim HG(8,5,3)$

초기하 분포 공식

초기하 분포에 대한 공식은 x 에 대한 K 의 조합 수를 nx 에 대한 NK 의 조합 수로 나누어 n 에 대한 N 의 조합 수를 곱한 것입니다.

여기서 N 은 모집단 크기, K 는 유리한 사례의 총 수, n 은 대체 없는 추출 수, x 는 발생 확률을 계산해야 하는 유리한 사례의 수입니다.

👉 아래 계산기를 사용하여 초기하 분포를 따르는 변수의 사건 확률을 계산할 수 있습니다.

초기하 분포의 예

초기하 분포의 정의와 공식을 살펴보았으면 이제 초기하 분포의 확률을 계산하는 방법을 알 수 있도록 예제를 단계별로 풀어보겠습니다.

가방 안에 파란색 공 20개, 빨간색 공 30개를 넣습니다. 즉, 가방 안에는 총 50개의 공이 들어 있습니다. 공 12개를 교체하지 않고 뽑을 경우 파란색 공 4개가 나올 확률을 구하세요.

연습 문제를 해결하기 위해 가장 먼저 해야 할 일은 초기하 분포의 매개변수를 식별하는 것입니다. 이 경우 모집단의 총 요소 수는 50개( N =50)이고, 유리한 경우의 최대 개수는 20개( K =20)이며, 12개의 공이 추첨됩니다( n =12).

$\left.\begin{array}{c}N=50\\[2ex]K=20\\[2ex]n=12\end{array}\right\} \longrightarrow \ X\sim HG(50,20,12)$

우리는 4개의 파란색 공( x =4)을 뽑을 확률을 계산하려고 하므로 초기하 분포 공식을 적용하고 변수를 해당 값으로 대체한 후 계산을 수행합니다.

$P\bigl[X=x\bigr]=\cfrac{\begin{pmatrix}K\\x\end{pmatrix}\begin{pmatrix}N-K\\n-x\end{pmatrix}}{\begin{pmatrix}N\\n\end{pmatrix}}$

$\begin{aligned}P\bigl[X=4\bigr]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}50-20\\12-4\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}30\\8\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=0,2336 \end{aligned}$

초기하 분포 계산기

초기하 분포의 매개변수를 다음 온라인 계산기에 입력하여 원하는 사건이 발생할 확률을 계산합니다.

N 은 모집단 크기, K 는 유리한 사례의 총 수, n 은 표본 크기, x 는 이러한 일이 발생할 확률을 구하려는 값이라는 점을 기억하세요.

초기하 분포의 특성

초기하 분포에는 다음과 같은 속성이 있습니다.

초기하 분포의 기대값은 표본의 요소 수에 유리한 케이스의 총 수를 모집단의 요소 수로 나눈 값과 같습니다.

$E[X]=\cfrac{n\cdot K}{N}$

초기하 분포의 최빈값은 n+1 곱하기 K+1 을 N+2 로 나눈 값에서 반올림된 값입니다.

$\displaystyle M=\Bigg\lfloor \frac{(n+1)(K+1)}{N+2}\Bigg\rfloor$

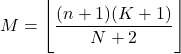
초기하 분포의 분산은 다음 표현식을 사용하여 얻을 수 있습니다.

$\displaystyle Var[X]=\cfrac{nK}{N}\left(\frac{N-K}{N}\right)\left(\frac{N-n}{N-1}\right)$

초기하 분포의 모멘트 생성 함수는 다음과 같습니다.

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K-n+1; e^{t}) } }{{N \choose n}}$

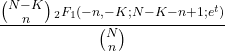
초기하 분포의 특성 함수는 다음과 같습니다.

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K - n + 1; e^{it}) }}{{N \choose n}}$

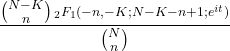
주어진 수의 사건이 발생할 확률은 초기하 분포에 대한 재귀를 사용하여 이전 수의 확률로부터 계산할 수 있습니다.

$P[X=x+1]=\cfrac{(K-x)(n-x)}{(x+1)(N-K-n+x-1)}\cdot P[X=x]$

초기하 분포 및 이항 분포

초기하 분포와 이항 분포의 차이점은 대체입니다. 초기하 분포는 검색이 대체되지 않을 때 사용되지만, 이항 분포 검색에서는 대체됩니다.

예를 들어, 덱에서 무작위로 5장의 카드를 뽑고 특정 카드를 얻을 확률을 계산하려는 경우 뽑은 각 카드를 교체하지 않으면 초기하 분포를 사용하여 계산을 수행해야 합니다. 그러나 카드를 제거할 때 다음 추출을 수행하기 전에 다시 넣어두면 확률을 계산하기 위해 이항 분포를 사용해야 합니다.

숫자 N 이 크고 n/N 비율이 작고 원하는 유리한 경우의 수가 매우 작을 때 초기하 분포를 이항 분포의 근사치로 사용할 수 있습니다. 그러나 결과가 그다지 신뢰할 수 없을 뿐만 아니라 초기하법칙보다 이항법칙을 사용하여 확률을 계산하는 것이 더 쉽기 때문에 권장하지 않습니다.

저자 소개

벤자민 앤더슨

안녕하세요. 저는 통계학 교수를 퇴직하고 전임 통계 교사로 변신한 벤자민입니다. 통계 분야의 광범위한 경험과 전문 지식을 바탕으로 Statorials를 통해 학생들에게 힘을 실어주기 위해 지식을 공유하고 싶습니다. 더 알아보기