카이제곱 분포

에 의해 벤자민 앤더슨 8월 4, 2023 개연성 댓글 0개

이 기사에서는 카이제곱 분포의 정의와 용도에 대해 설명합니다. 또한 카이제곱 분포 그래프와 해당 속성을 찾을 수 있습니다.

카이제곱 분포란 무엇입니까?

카이제곱 분포는 기호가 χ²인 확률 분포입니다. 보다 정확하게는 카이제곱 분포는 k개의 독립 확률 변수의 제곱을 정규 분포와 합한 것입니다.

따라서 카이제곱 분포는 k 개의 자유도를 갖습니다. 따라서 카이제곱 분포는 그것이 나타내는 정규 분포 변수의 제곱의 합만큼 많은 자유도를 갖습니다.

$\displaystyle X\sim\chi^2_k \ \color{orange}\bm{\longrightarrow}\color{black}\ \begin{array}{l}\text{Distribuci\'on chi-cuadrado}\\[2ex]\text{con k grados de libertad}\end{array}$

카이제곱 분포는 피어슨 분포 라고도 합니다.

카이제곱 분포는 감마 분포의 특별한 경우라는 점에 유의해야 합니다.

카이제곱 분포는 가설 검정 및 신뢰 구간과 같은 통계적 추론에 널리 사용됩니다. 이러한 유형의 확률 분포가 어떻게 적용되는지 아래에서 살펴보겠습니다.

카이제곱 분포 그래프

카이제곱 분포의 정의를 확인한 후에는 이러한 유형의 분포가 그래픽으로 표현된 몇 가지 예를 볼 수 있습니다. 아래에서는 카이제곱 분포의 확률도가 자유도에 따라 어떻게 달라지는지 확인할 수 있습니다.

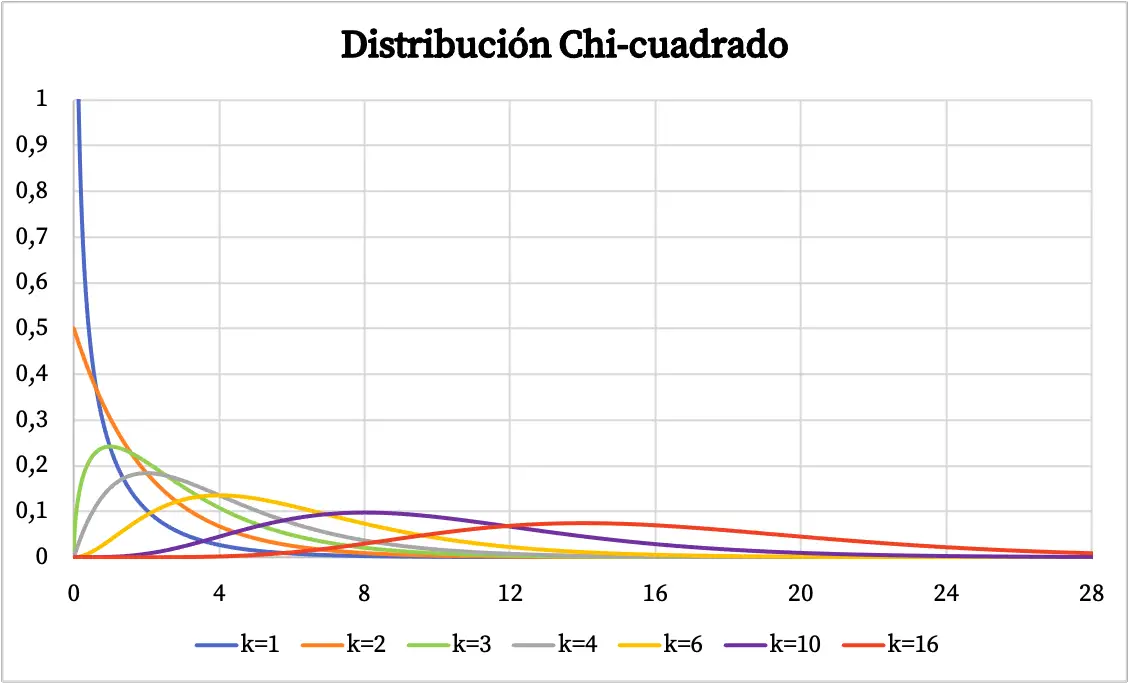
카이제곱 분포의 밀도 함수는 위 그래프에 표시되어 있습니다. 한편, 카이제곱 누적확률분포함수의 그래프는 다음과 같다.

➤ 참조: 카이제곱 분포표

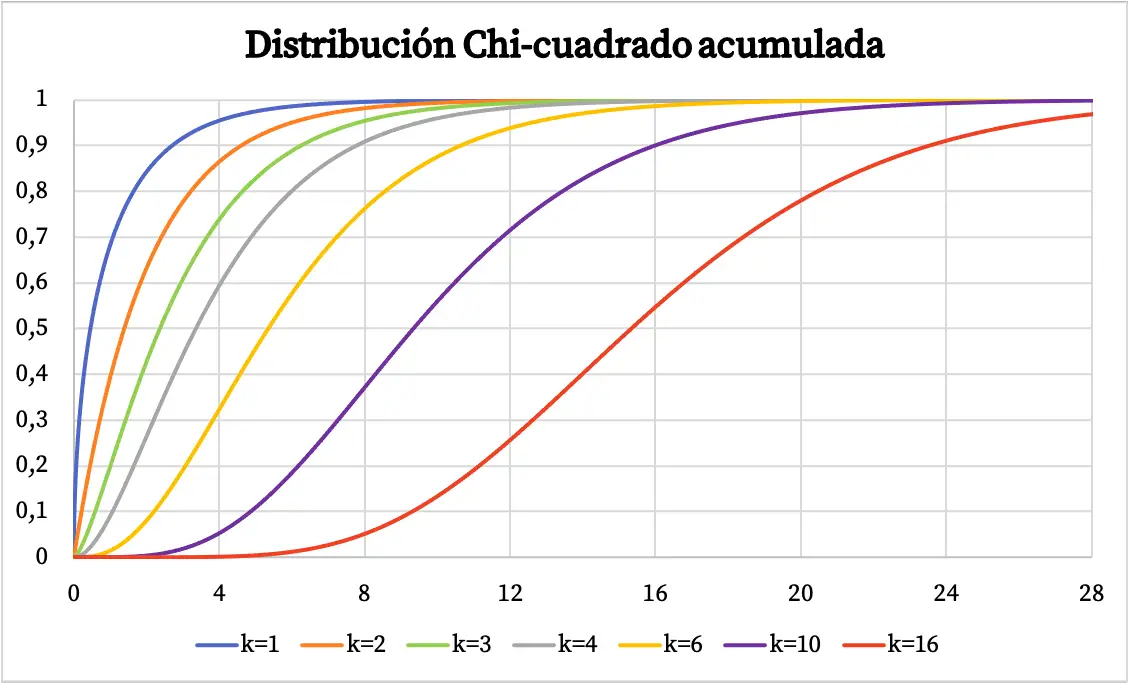
카이제곱 분포의 특성

이 섹션에서는 확률 이론 및 통계와 관련된 카이제곱 분포의 가장 중요한 속성을 살펴보겠습니다.

카이제곱 분포의 평균은 자유도와 같습니다.

$\begin{array}{c}X\sim\chi^2_k\\[2ex] E[X]=k\end{array}$

카이제곱 분포의 분산은 분포 자유도의 두 배와 같습니다.

$\begin{array}{c}X\sim\chi^2_k\\[2ex] Var(X)=2\cdot k\end{array}$

카이제곱 분포의 모드는 분포의 자유도가 1보다 크면 자유도보다 2단위 작습니다.

$Mo=k-2 \qquad \text{si } k\geq 2$

카이제곱 분포의 밀도 함수는 x=0인 경우 0입니다. 그러나 0보다 큰 x 값의 경우 카이제곱 분포의 밀도 함수는 다음 공식으로 정의됩니다.

$\displaystyle P[X=x]= \frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2}$

카이제곱 분포의 누적 분포 함수는 다음 공식으로 결정됩니다.

$\displaystyle P[X\leq x]=\frac{\gamma(k/2,x/2)}{\Gamma(k/2)}$

카이제곱 분포의 왜도 계수는 몫 8을 분포의 자유도 수로 나눈 값의 제곱근입니다.

$\displaystyle A=\sqrt{\frac{8}{k}}$

카이제곱 분포의 첨도는 다음 식을 사용하여 계산됩니다.

$C=3+\cfrac{12}{k}$

중심 극한 정리로 인해 카이제곱 분포는 k 가 충분히 크면 정규 분포로 근사화될 수 있습니다.

$\displaystyle\lim_{k \to \infty} \frac{\chi^2_k (x)}{ k } = N_{\left(1,\sqrt{2/k}\right)} (x)$

카이제곱 분포의 응용

카이제곱 분포는 통계에서 다양한 용도로 사용됩니다. 실제로 변수 간의 독립성과 이론적 분포에 대한 적합성을 확인하는 데 사용되는 카이제곱 검정도 있습니다. 예를 들어, 카이제곱 검정을 사용하여 표본 데이터가 포아송 분포를 따르는지 여부를 확인할 수 있습니다.

선형 회귀 분석에서 카이제곱 분포는 정규 분포 모집단의 평균을 추정하고 선형 회귀 연구 선의 기울기를 추정하는 데에도 사용됩니다.

마지막으로 카이 제곱 분포는 Snedecor F 분포와의 관계를 통해 분산 분석에도 참여합니다.

저자 소개

벤자민 앤더슨

안녕하세요. 저는 통계학 교수를 퇴직하고 전임 통계 교사로 변신한 벤자민입니다. 통계 분야의 광범위한 경험과 전문 지식을 바탕으로 Statorials를 통해 학생들에게 힘을 실어주기 위해 지식을 공유하고 싶습니다. 더 알아보기