Excel에서 카이 제곱 적합 테스트를 수행하는 방법
카이제곱 적합도 검정은 범주형 변수가 가상 분포를 따르는지 여부를 확인하는 데 사용됩니다.
이 자습서에서는 Excel에서 카이제곱 적합도 테스트를 수행하는 방법을 설명합니다.
예: Excel의 카이제곱 적합도 검정
한 상점 주인은 매주 같은 수의 고객이 자신의 상점을 방문한다고 말합니다. 이 가설을 테스트하기 위해 독립적인 연구원이 특정 주에 매장에 오는 고객 수를 기록하고 다음을 알아냈습니다.
- 월요일: 고객 50명
- 화요일: 고객 60명
- 수요일: 고객 40명
- 목요일: 고객 47명
- 금요일: 고객 53명
다음 단계를 사용하여 카이제곱 적합도 테스트를 수행하여 데이터가 매장 소유자의 주장과 일치하는지 확인합니다.
1단계: 데이터를 입력합니다.
먼저 한 열에는 매일 예상 고객 수에 대한 데이터 값을 입력하고 다른 열에는 매일 관찰된 고객 수에 대한 데이터 값을 입력합니다.
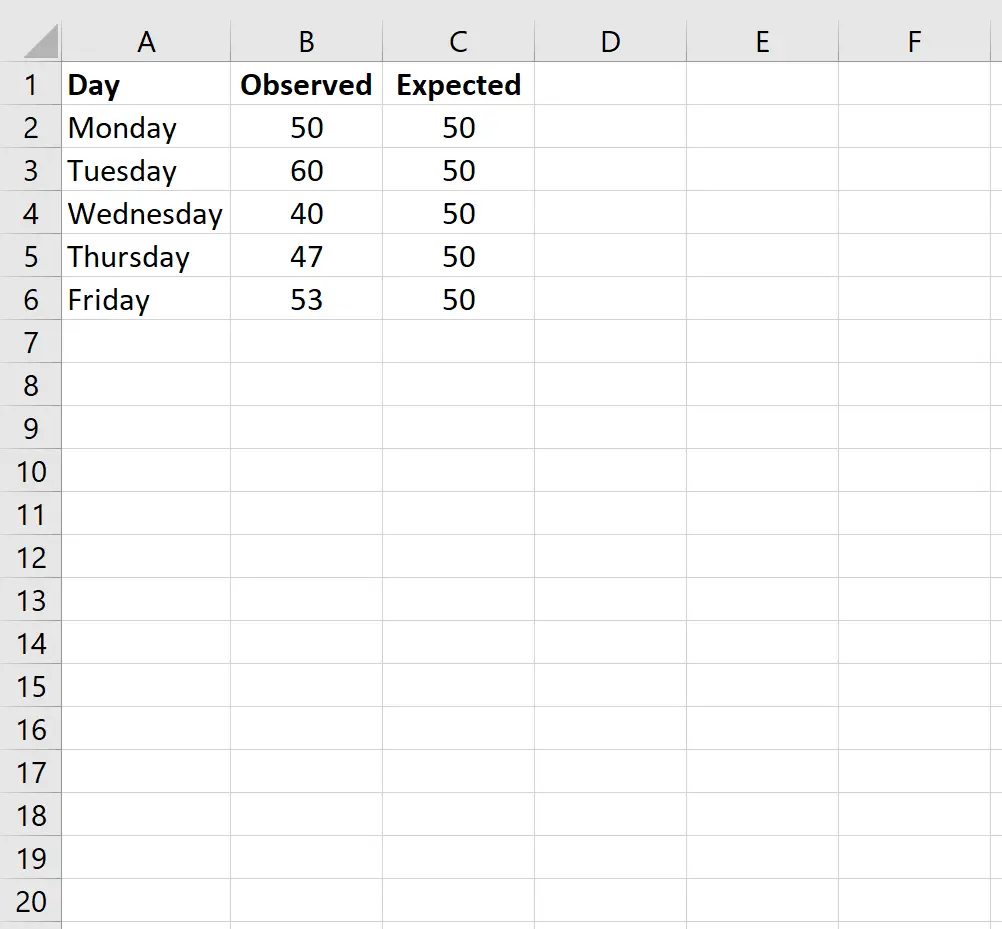
참고: 총 250명의 고객이 있었습니다. 따라서 상점 주인이 매일 같은 수의 고객이 상점에 들어올 것으로 예상한다면 하루에 50명의 고객이 있을 것으로 예상할 수 있습니다.
2단계: 관찰된 값과 예상된 값의 차이를 찾습니다.
적합도 검정에 대한 카이제곱 검정 통계량은 X 2 = Σ(OE) 2 / E 입니다.
금:
- Σ: “합”을 의미하는 화려한 기호입니다.
- O: 관측값
- E: 기대값
다음 공식은 각 행에 대해 (OE) 2 /E를 계산하는 방법을 보여줍니다.
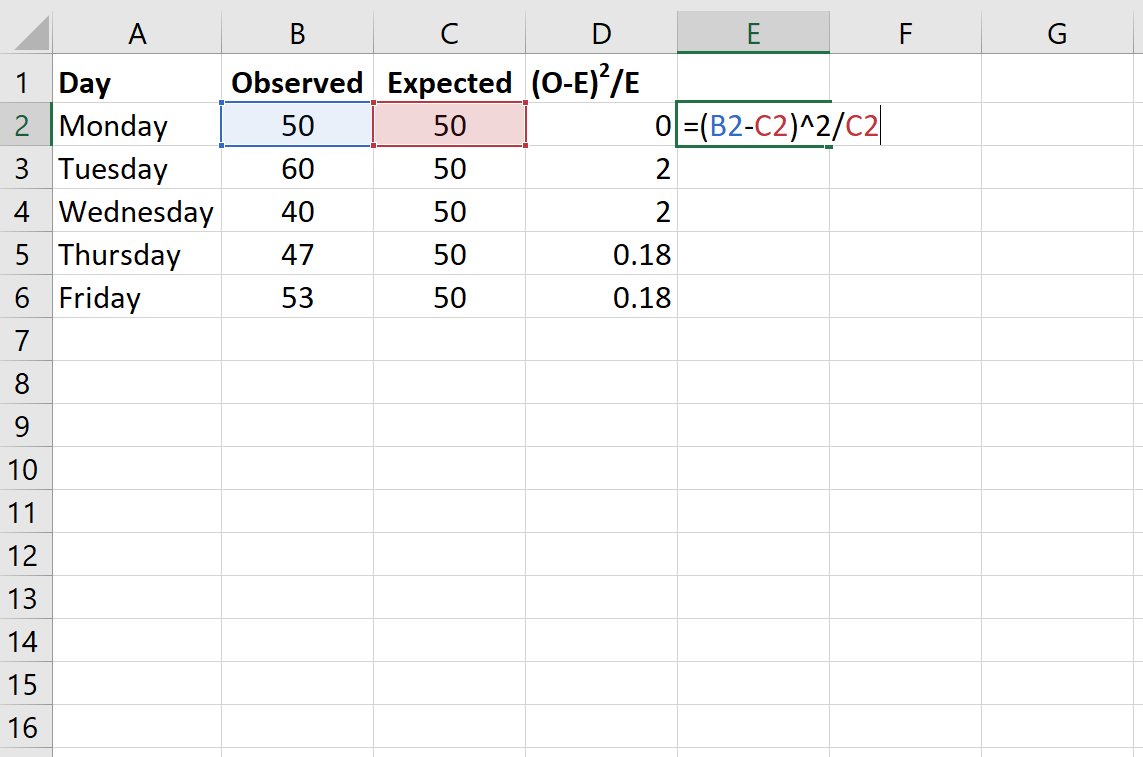
3단계: 카이제곱 검정 통계량과 해당 p-값을 계산합니다.
마지막으로 다음 공식을 사용하여 카이제곱 검정 통계량과 해당 p-값을 계산합니다.
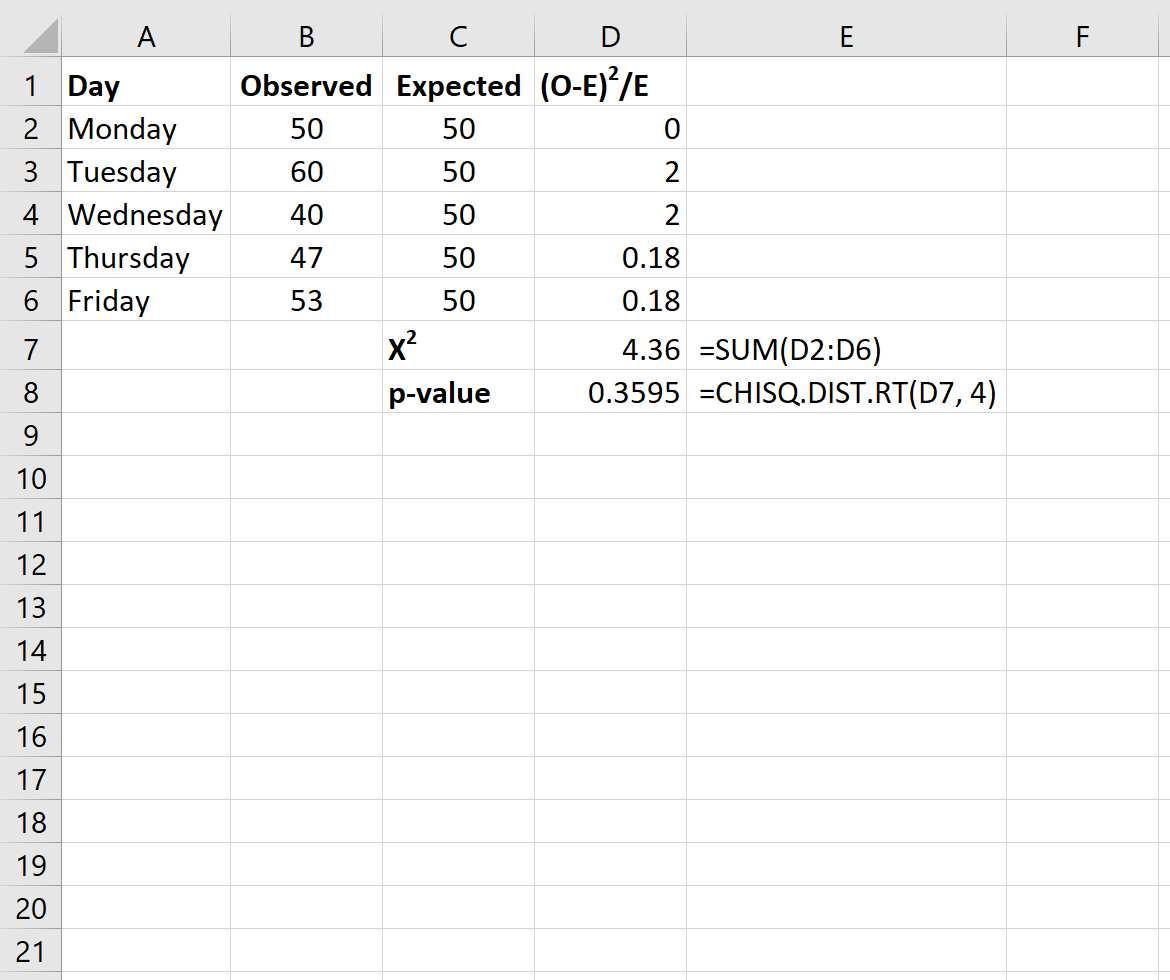
참고: Excel 함수 CHISQ.DIST.RT(x, deg_freedom)는 검정 통계량 x 및 특정 자유도와 연관된 카이 제곱 분포의 올바른 확률을 반환합니다. 자유도는 n-1로 계산됩니다. 이 경우 deg_freedom = 5 – 1 = 4입니다.
4단계: 결과를 해석합니다.
검정에 대한 X2 검정 통계량은 4.36 이고 해당 p-값은 0.3595 입니다. 이 p-값은 0.05 이상이므로 귀무가설을 기각할 수 없습니다. 이는 실제 고객 분포가 매장 주인이 보고한 분포와 다르다고 말할 수 있는 충분한 증거가 없음을 의미합니다.