파레토 분포
이 기사에서는 통계에서 파레토 분포가 무엇인지, 그리고 어떤 용도로 사용되는지 설명합니다. 또한 파레토 분포 그래프와 이러한 유형의 확률 분포의 속성을 볼 수 있습니다.
파레토 분포란 무엇입니까?
파레토 분포는 통계에서 파레토 원리를 모형화하는 데 사용되는 연속 확률 분포입니다. 따라서 파레토 분포는 나머지 값보다 발생 확률이 훨씬 높은 몇 가지 값을 갖는 확률 분포입니다.
80-20 법칙이라고도 불리는 파레토의 법칙은 현상의 대부분 원인이 소수의 인구에 기인한다는 통계적 원리라는 것을 기억하세요.
파레토 분포에는 척도 매개변수 x m 과 모양 매개변수 α라는 두 가지 특성 매개변수가 있습니다.
![]()
원래 파레토 분포는 인구 내 부의 분포를 설명하는 데 사용되었습니다. 그 이유는 부의 대부분이 인구의 작은 부분에 기인하기 때문입니다. 그러나 현재 파레토 분포는 품질 관리, 경제, 과학, 사회 분야 등 다양한 분야에 적용됩니다.
파레토 분포는 이 분포를 공식화한 경제학자 빌프레도 파레토(Vilfredo Pareto)의 이름을 따서 명명되었습니다. 그러나 그는 파레토 차트로 가장 잘 알려져 있습니다.
파레토 분포표
이제 파레토 분포의 정의를 알았으니 그래픽으로 표현된 파레토 분포의 몇 가지 예를 살펴보겠습니다.
따라서 아래에서 파레토 분포의 밀도 함수 그래프가 특성 값에 따라 어떻게 보이는지 확인할 수 있습니다.
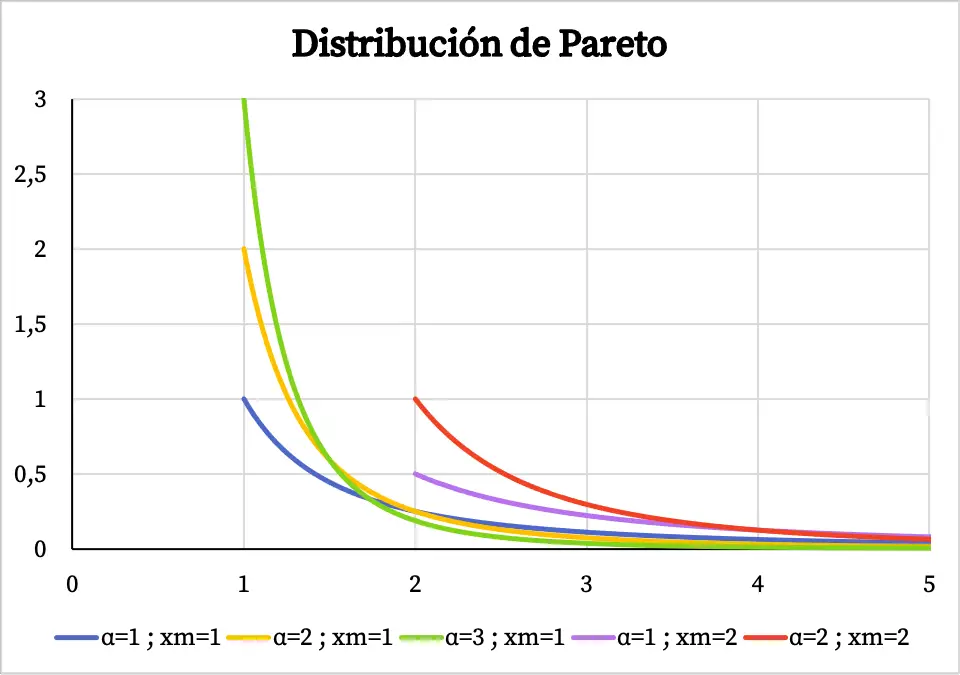
파레토 분포의 영역은 x m 값에서 +무한까지이며, 이는 밀도 함수가 x m 값 이전에 존재하지 않는 이유입니다.
한편, 파레토 분포의 누적확률함수 그래프는 다음과 같다.
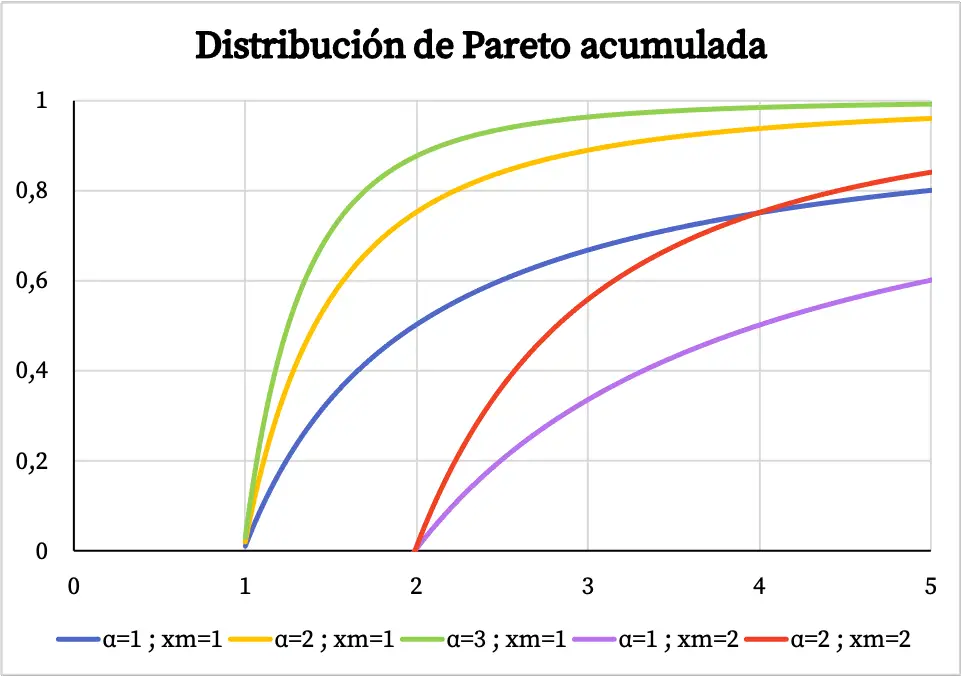
파레토 분포의 특성
확률론 및 통계와 관련된 파레토 분포의 가장 중요한 특징은 다음과 같습니다.
- 파레토 분포에는 곡선을 정의하는 두 가지 특성 매개변수인 척도 매개변수 x m 과 모양 매개변수 α가 있습니다.
![]()
- 파레토 분포의 영역은 척도 모수부터 플러스 무한대까지의 모든 실수로 구성됩니다.
![]()
- α가 1보다 큰 경우 파레토 분포의 평균은 α에 xm을 곱하고 α에서 1을 뺀 값과 같습니다.
![E[X]=\cfrac{\alpha\cdot x_m}{\alpha-1}\quad\text{para } \alpha>1″ title=”Rendered by QuickLaTeX.com” height=”34″ width=”214″ style=”vertical-align: -12px;”></p>
</p>
<ul>
<li> 파레토 분포의 분산은 분포의 두 가지 특성 매개변수에 따라 달라지며 다음 공식으로 계산됩니다.</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-6d26513868f9ed6fa45ab0fde0030884_l3.png)
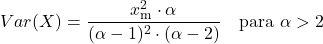
![]()
- 파레토 분포의 최빈값은 분포의 척도 모수 x m 과 동일합니다.
![]()
- 파레토 분포의 밀도 함수 공식은 다음과 같습니다.
![]()
- 마찬가지로 파레토 분포의 누적 확률 함수 공식은 다음과 같습니다.
![]()
- 파레토 분포의 비대칭 계수는 형상 매개변수 α에만 의존하며 그 표현은 다음과 같습니다.
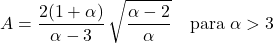
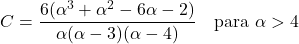
저자 소개
벤자민 앤더슨
안녕하세요. 저는 통계학 교수를 퇴직하고 전임 통계 교사로 변신한 벤자민입니다. 통계 분야의 광범위한 경험과 전문 지식을 바탕으로 Statorials를 통해 학생들에게 힘을 실어주기 위해 지식을 공유하고 싶습니다. 더 알아보기