Sas에서 일원 분산 분석을 수행하는 방법

일원 분산 분석은 3개 이상의 독립 그룹 평균 간에 통계적으로 유의한 차이가 있는지 여부를 확인하는 데 사용됩니다.

이 튜토리얼에서는 SAS에서 일원 분산 분석을 수행하는 방법에 대한 단계별 예를 제공합니다.

1단계: 데이터 생성

한 연구자가 연구에 참여할 학생 30명을 모집한다고 가정해 보겠습니다. 학생들은 시험 준비를 위해 세 가지 학습 방법 중 하나를 사용하도록 무작위로 배정 됩니다.

각 학생의 시험 결과는 다음과 같습니다.

다음 코드를 사용하여 SAS에서 이 데이터 세트를 생성할 수 있습니다.

 /*create dataset*/
data my_data;
    input Method $Score;
    datalines ;
At 78
At 81
At 82
At 82
At 85
At 88
At 88
At 90
B 81
B 83
B 83
B85
B 86
B 88
B90
B91
C 84
C 88
C 88
C 89
C 90
C 93
C 95
C 98
;
run ;

2단계: 일원 분산 분석 수행

다음으로 proc ANOVA를 사용하여 일원 분산 분석을 수행합니다.

 /*perform one-way ANOVA*/
proc ANOVA data =my_data;
classMethod ;
modelScore = Method;
means Method / tukey cldiff ;
run ;

참고 : 일원 분산 분석의 전체 p-값이 통계적으로 유의한 경우 Tukey 사후 테스트를 수행해야 함을 지정하기 위해 평균 함수를 사용했습니다.

3단계: 결과 해석

결과에서 분석하려는 첫 번째 테이블은 ANOVA 테이블입니다.

이 표에서 우리는 다음을 볼 수 있습니다:

• 전체 F값: 5.26
• 해당 p-값: 0.0140

일원 분산 분석에서는 다음과 같은 귀무 가설과 대립 가설을 사용합니다.

• H ₀ : 모든 그룹 평균이 동일합니다.
• H _A : 적어도 하나의 그룹 평균이 다릅니다.   나머지.

ANOVA 테이블의 p-값(0.0140)이 α = 0.05보다 작으므로 귀무 가설을 기각합니다.

이는 세 가지 학습 방법의 평균 시험 점수가 동일하지 않음을 나타냅니다.

관련 항목: ANOVA에서 F-값과 P-값을 해석하는 방법

SAS는 또한 세 가지 학습 방법 각각에 대한 시험 결과 분포를 시각화하는상자 그림을 제공합니다.

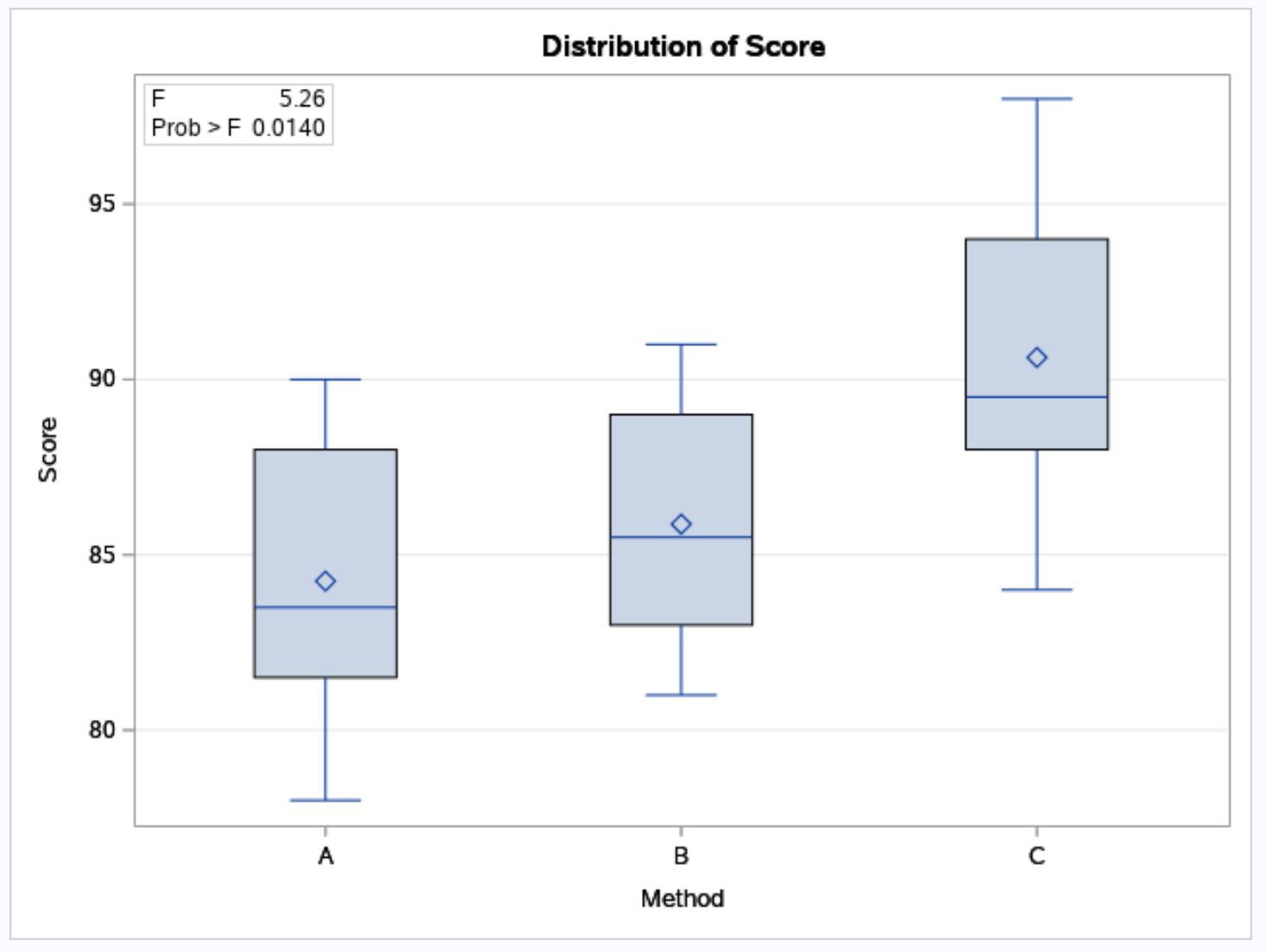
상자 그림을 보면 학습 방법 B와 C에 비해 C 방법을 사용한 학생의 시험 점수가 더 높은 경향이 있음을 알 수 있습니다.

정확히 어떤 그룹 평균이 다른지 확인하려면 Tukey의 사후 테스트 결과를 보여주는 최종 결과 테이블을 참조해야 합니다.

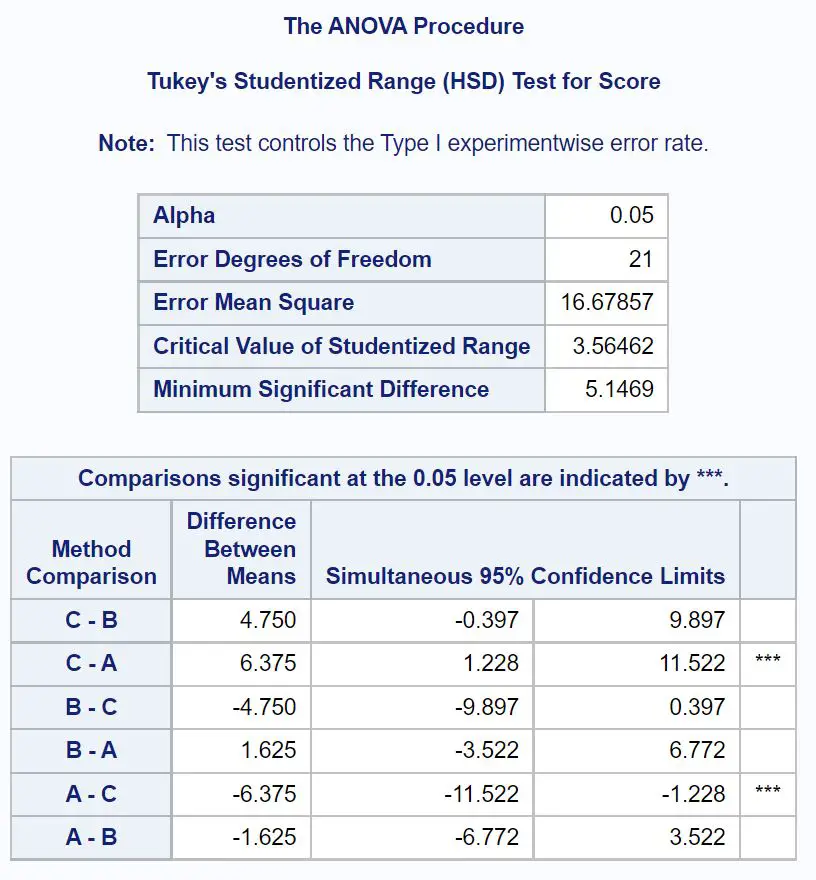
어떤 그룹 평균이 다른지 확인하려면 옆에 별표( *** )가 있는 쌍별 비교를 살펴봐야 합니다.

표를 보면 그룹 A와 C의 평균값이 통계적으로 유의하게 다른 것을 알 수 있습니다.

또한 그룹 A와 C 간의 평균 시험 점수 차이에 대한 95% 신뢰 구간을 볼 수 있습니다.

평균 차이에 대한 95% 신뢰 구간: [1.228, 11.522]

4단계: 결과 보고

마지막으로 일원 분산 분석의 결과를 보고 할 수 있습니다.

세 가지 다른 연구 방법이 검사 결과에 미치는 영향을 비교하기 위해 일원 분산 분석(one-way ANOVA)을 수행했습니다.

일원 분산 분석(one-way ANOVA)을 통해 최소 두 그룹 간의 평균 시험 점수에 통계적으로 유의미한 차이가 있는 것으로 나타났습니다(F(2,21) = [5.26], p = 0.014).

다중 비교를 위한 Tukey의 HSD 테스트에서는 시험 점수의 평균값이 방법 C와 방법 A 간에 크게 다른 것으로 나타났습니다(95% CI = [1.228, 11.522]).

방법 A와 방법 B, 방법 B와 방법 C 사이의 평균 시험 점수에는 통계적으로 유의미한 차이가 없었습니다.

추가 리소스

다음 자습서에서는 일원 분산 분석에 대한 추가 정보를 제공합니다.

일원 분산 분석 소개
일원 분산 분석 계산기
일원 분산 분석을 수동으로 수행하는 방법