Stata에서 일원 분산 분석을 수행하는 방법

일원 분산 분석은 3개 이상의 독립 그룹 평균 간에 통계적으로 유의한 차이가 있는지 여부를 확인하는 데 사용됩니다.

이러한 유형의 테스트는 예측 변수가 반응 변수에 미치는 영향을 분석하기 때문에 일원 분산 분석이라고 합니다. 대신 두 예측 변수가 반응 변수에 미치는 영향에 관심이 있다면 양방향 ANOVA를 수행할 수 있습니다.

이 튜토리얼에서는 Stata에서 일원 분산 분석을 수행하는 방법을 설명합니다.

예: Stata의 일원 분산 분석

이 예에서는 systolic 이라는 내장 Stata 데이터 세트를 사용하여 일원 분산 분석을 수행합니다. 이 데이터 세트에는 58명의 개인에 대한 다음 세 가지 변수가 포함되어 있습니다.

• 사용된 약물
• 환자의 질병
• 수축기 혈압의 변화

우리는 다음 단계를 사용하여 일원 분산 분석을 수행하여 사용된 약물 유형이 수축기 혈압 변화에 중요한 영향을 미치는지 확인합니다.

1단계: 데이터를 로드합니다.

먼저 명령 상자에 webuse systolic을 입력하고 Enter를 클릭하여 데이터를 로드합니다.

2단계: 원시 데이터를 봅니다.

일원 분산 분석을 수행하기 전에 먼저 원시 데이터를 살펴보겠습니다. 상단 메뉴바에서 데이터 > 데이터 편집기 > 데이터 편집기(찾아보기) 로 이동합니다. 그러면 58명의 환자 모두에 대한 실제 데이터가 표시됩니다.

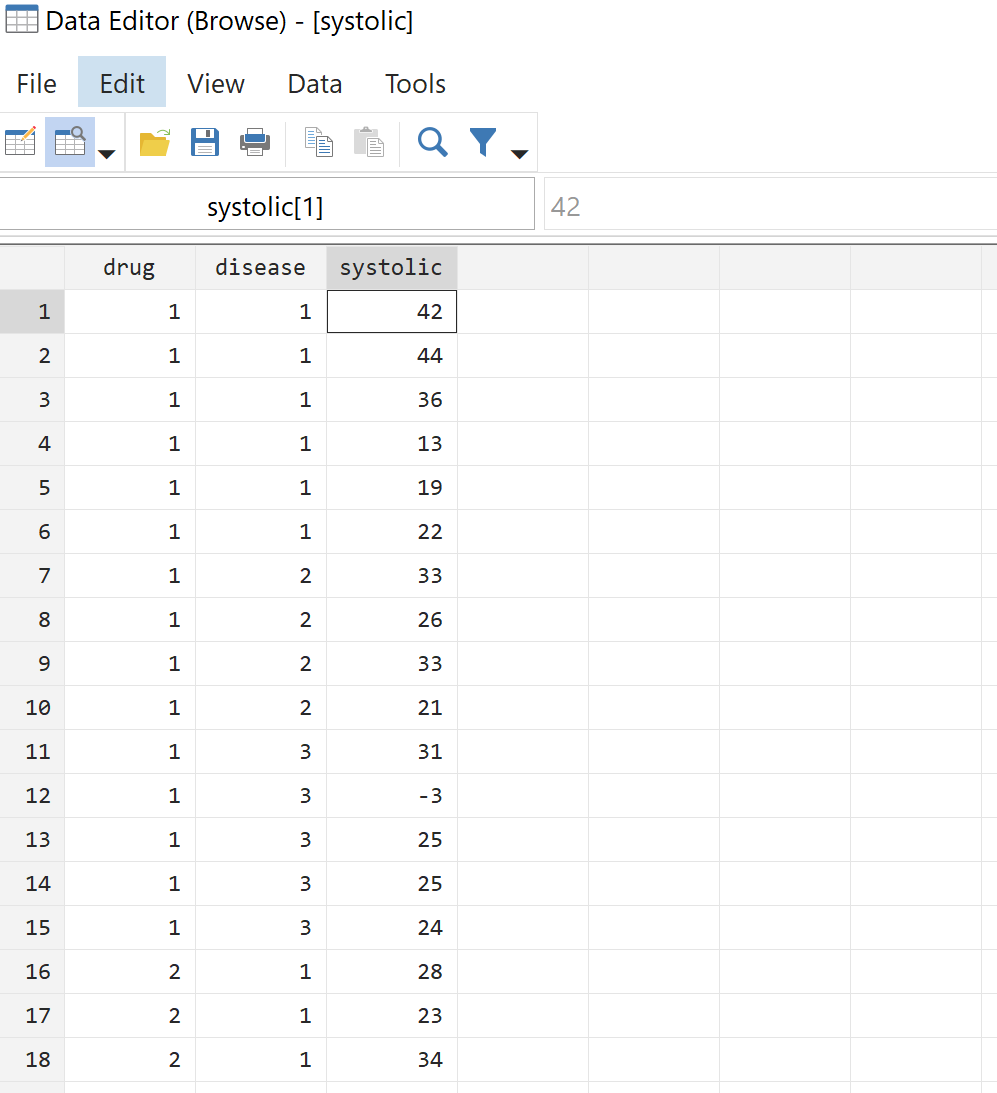
3단계: 데이터를 시각화합니다.

다음으로 데이터를 시각화해 보겠습니다. 각 약물 카테고리에 대한 수축기 혈압 값의 분포를 표시하기 위해상자 그림을 만듭니다.

상단 메뉴 표시줄에서 차트 > 상자 그림 으로 이동합니다. 변수에서 Systolic을 선택합니다.

그런 다음 그룹화 변수 아래의 범주 하위 제목에서 약물을 선택합니다.

확인 을 클릭합니다. 4개의 상자 그림이 있는 차트가 자동으로 표시됩니다.

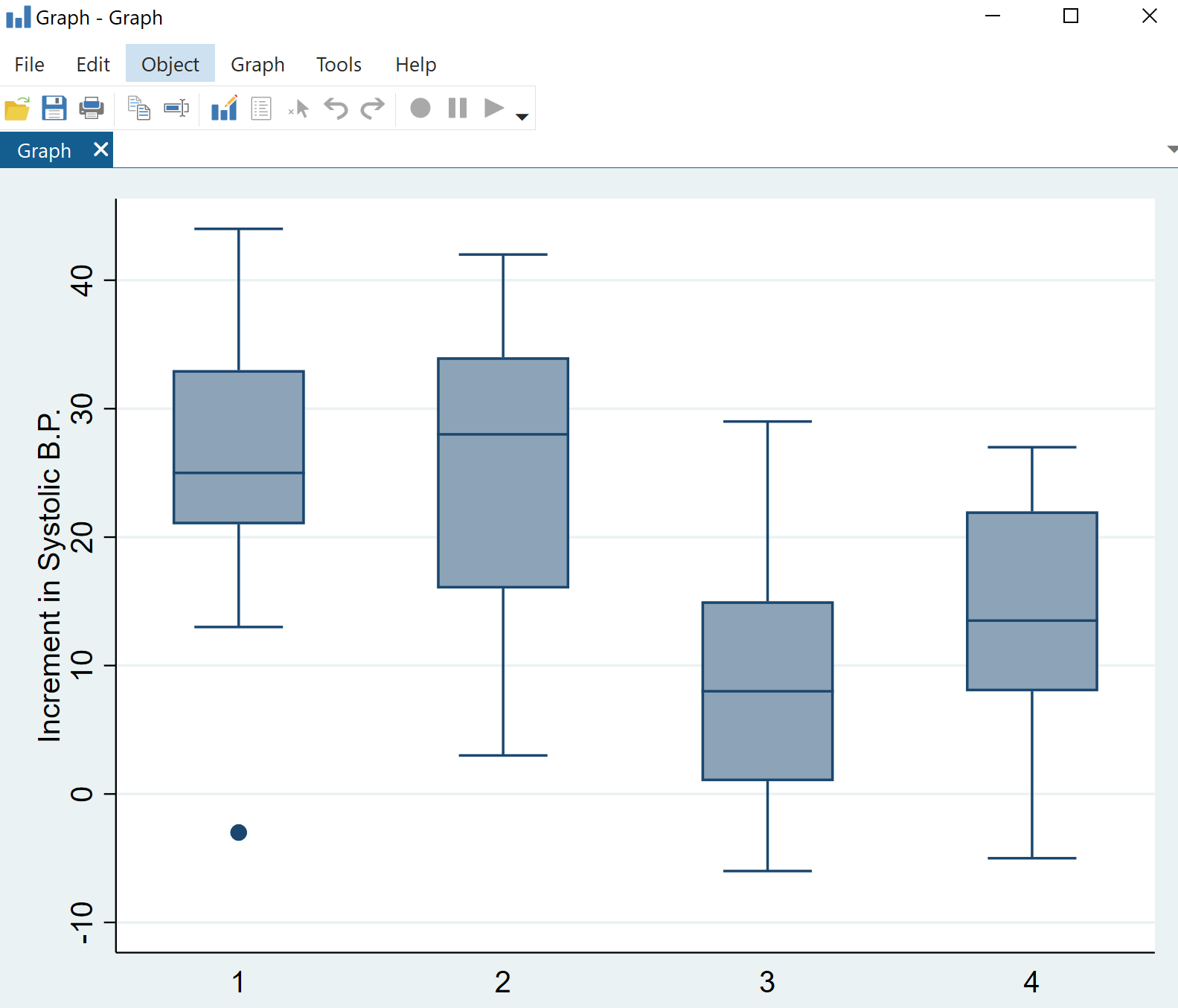
수축기 혈압의 변화 분포가 약물 범주에 따라 다양하다는 것을 즉시 확인할 수 있지만 일원 분산 분석을 통해 이러한 차이가 통계적으로 유의한지 여부를 알 수 있습니다.

4단계: 일원 분산 분석을 수행합니다.

상단 메뉴 표시줄에서 통계 > 선형 및 관련 모형 > ANOVA/MANOVA > 일원 분산 분석 으로 이동합니다.

응답 변수에서 Systolic을 선택합니다. 요인 변수에서 약물을 선택합니다. 그런 다음 요약표 생성 옆에 있는 상자를 클릭하면 각 그룹에 대한 몇 가지 기본 설명 통계를 볼 수 있습니다. 그런 다음 확인을 클릭합니다.

다음 출력이 표시됩니다.

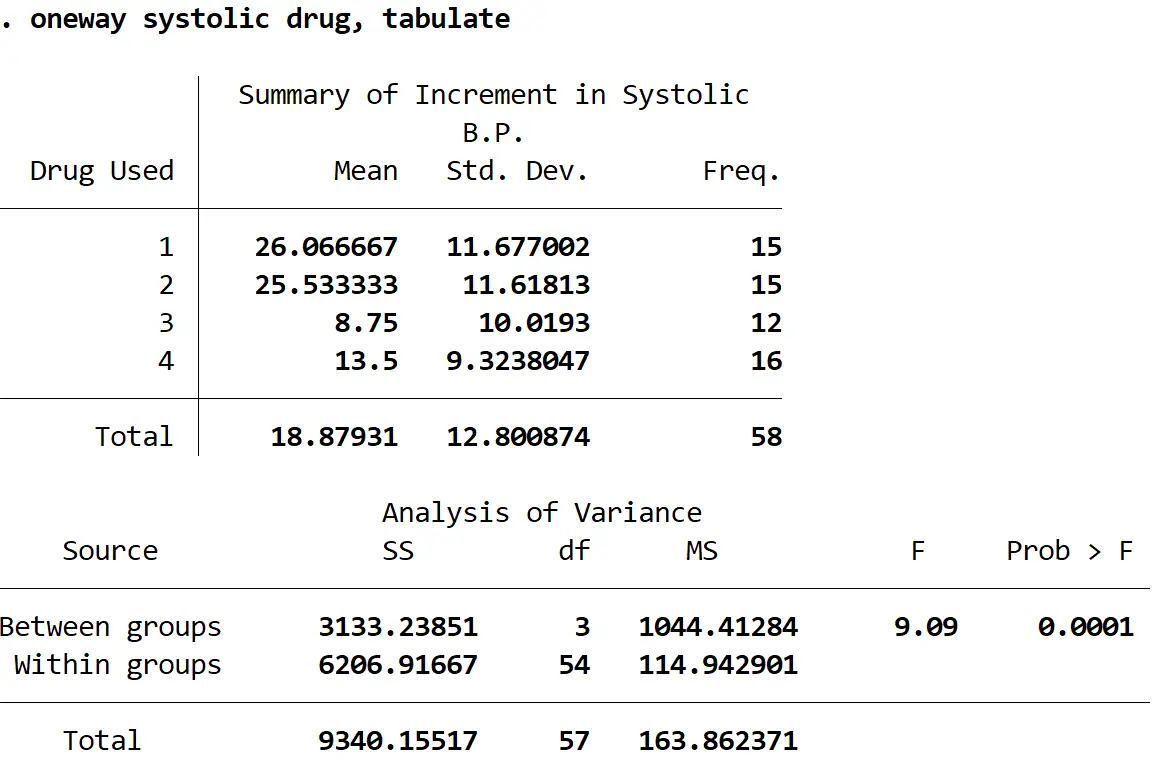
F 통계량은 9.09 이고 해당 p-값은 0.0001 입니다. p-값이 알파 = 0.05보다 작기 때문에 각 그룹의 평균 수축기 혈압 변화가 동일하다는 귀무가설을 기각할 수 있습니다.

즉, 적어도 두 약물군 간에 수축기 혈압의 평균 변화에 통계적으로 유의미한 차이가 있습니다.

5단계: 여러 비교 테스트를 실행합니다.

그런 다음 몇 가지 비교 테스트를 실행하여 실제로 어떤 그룹 평균이 서로 다른지 알아낼 수 있습니다.

상단 메뉴 표시줄에서 통계 > 요약, 표 및 검정 > 요약 및 기술 통계 > 평균 쌍별 비교 로 이동합니다 .

변수에서 수축기 응답 변수를 선택합니다. 초과의 경우 설명 변수 drug 를 선택합니다. 다중 비교 조정에서 Tukey 방법을 선택합니다.

그런 다음 보고 하위 제목 아래에서 효과 표 옆에 있는 버튼을 클릭하고 신뢰 구간 및 p-값과 함께 효과 표 표시 옆의 확인란을 선택합니다. 그런 다음 확인을 클릭합니다.

다음 결과가 표시됩니다.

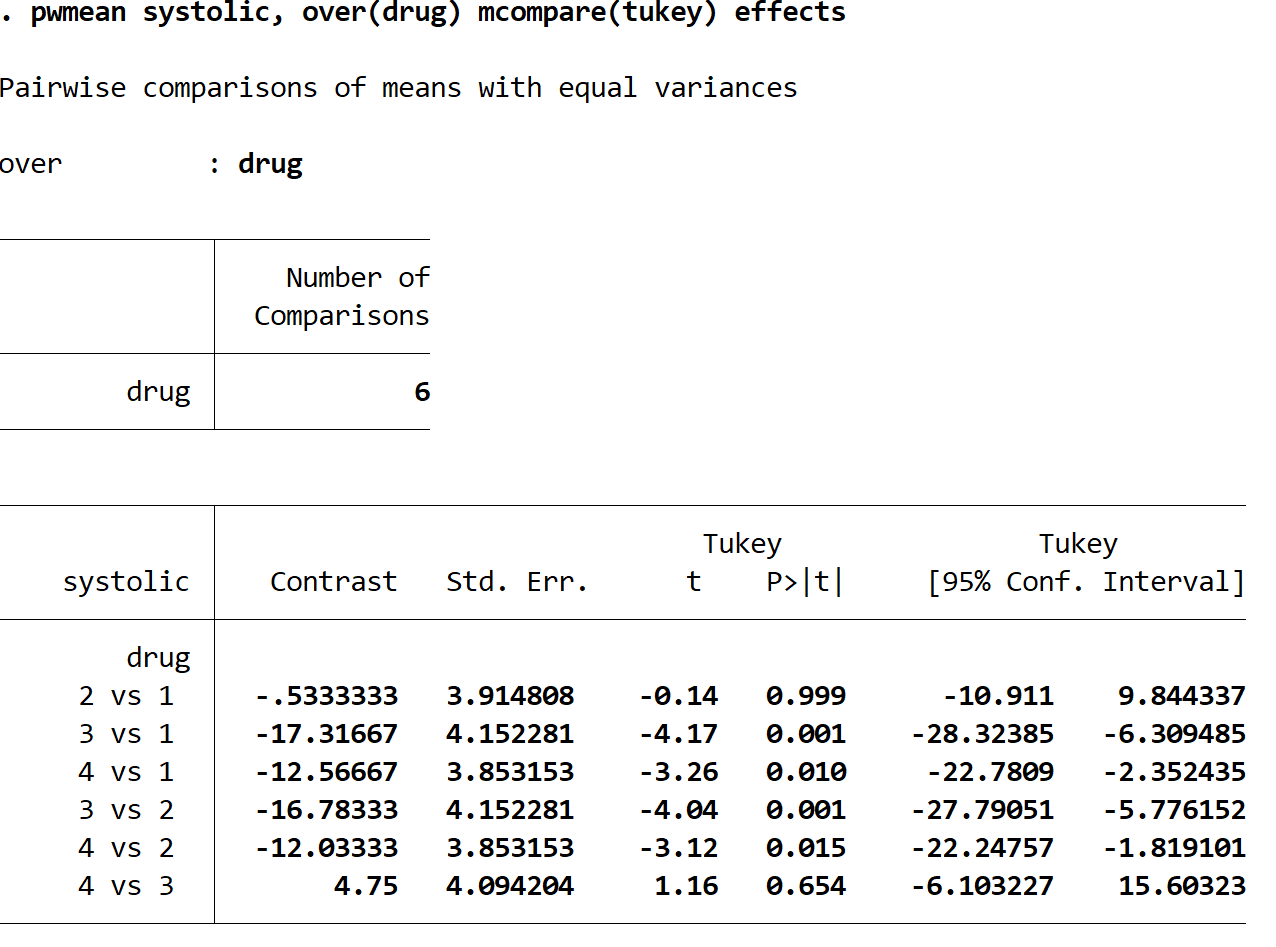
각 행은 두 가지 특정 약물 그룹 간의 비교를 나타냅니다. 예를 들어, 첫 번째 행은 약물 그룹 2와 약물 그룹 1 사이의 수축기 혈압의 평균 변화를 비교합니다. 이 비교에 대한 p-값은 0.999 로, 이는 0.05 이상으로 매우 높습니다. 이는 약물군 1과 2 사이에 통계적으로 유의미한 차이가 없음을 의미합니다.

그러나 다음 비교에 대한 p-값은 모두 0.05 미만임을 알 수 있습니다.

• 약 3 대 1 | p-값 = 0.001
• 약 4 대 1 | p-값 = 0.010
• 2에 대한 약 3 | p-값 = 0.001
• 2에 대한 약 4 | p-값 = 0.015

이는 수축기 혈압의 평균 변화 차이가 각 그룹 간에 통계적으로 유의미하다는 것을 의미합니다.

6단계: 결과를 보고합니다.

마지막으로 일원 분산 분석(one-way ANOVA) 분석 결과를 보고하겠습니다. 이를 수행하는 방법의 예는 다음과 같습니다.

네 가지 유형의 약물이 수축기 혈압에 서로 다른 영향을 미치는지 여부를 확인하기 위해 일원 분산 분석(one-way ANOVA)을 수행했습니다.

다음 표에는 각 그룹의 참가자 수와 각 그룹의 수축기 혈압의 평균 변화 및 수축기 혈압의 표준 편차가 요약되어 있습니다.

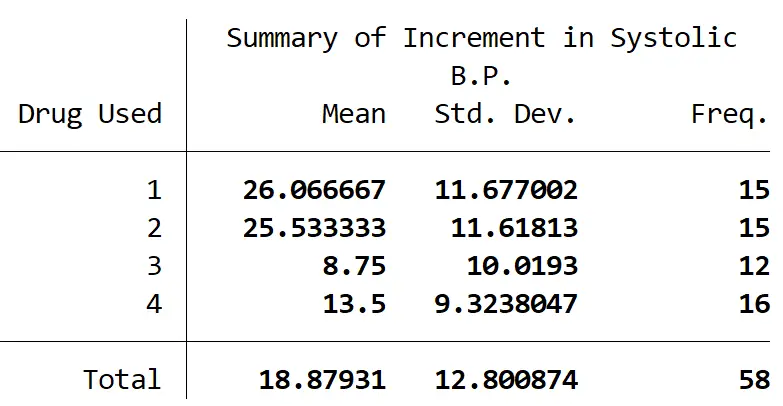
일원 분산 분석(one-way ANOVA)을 통해 적어도 두 그룹 간에 통계적으로 유의한 차이가 있는 것으로 나타났습니다(F(3, 54) = 9.09, p = 0.001).

다중 비교를 위한 Tukey 테스트에서는 수축기 혈압의 변화가 약물 1에 비해 약물 3에서 통계적으로 유의하게 높았고(17.32 +/- 4.15, p = 0.001), 약물 2에 비해 약물 3에서(16.78 +/- 4.15, p = 0.001), 약물 4의 경우 약물 1과 비교(12.57 +/- 3.85, p = 0.010), 약물 4의 경우 약물 2와 비교(12.03 +/- 3.85, p = 0.015).

약물군 1과 2(0.533 ± 3.91, p = 0.999) 또는 약물군 3과 4(4.75 ± 4.09, p = 0.654) 간에는 통계적으로 유의한 차이가 없었습니다.