표본의 크기
이 기사에서는 표본 크기가 무엇인지, 이것이 통계에서 중요한 이유를 설명합니다. 또한 적절한 표본 크기를 계산하는 방법과 해결 방법을 알아보고 이것이 어떻게 수행되는지 확인할 수 있습니다.
표본 크기는 얼마입니까?
표본 크기 (또는 표본 크기 )는 연구 표본을 구성하는 개인의 수입니다. 통계에서는 표본이 전체 모집단을 대표할 수 있도록 표본 크기가 중요합니다.
따라서 통계 연구의 표본 크기는 전체 모집단의 특성을 대표할 수 있을 만큼 충분히 커야 합니다. 반면에, 연구 비용이 더 많이 들기 때문에 표본 크기가 지나치게 클 수는 없습니다. 결론적으로 표본의 크기는 너무 크지도 작지도 않게 적당해야 합니다.
예를 들어, 한 국가의 키에 대한 분석을 하고 싶다면 그 나라의 모든 주민의 키를 물어볼 수는 없습니다. 그 이유는 조사 시간이 오래 걸리고 비용이 너무 많이 들기 때문입니다. 그러므로 무작위 표본추출을 수행하고 모집단을 대표하는 표본만을 인터뷰하는 것이 필요합니다.
그리고 적절한 표본 크기를 어떻게 알 수 있습니까? 다음 섹션에서는 연구 요구 사항에 따라 적절한 표본 크기를 결정하는 방법을 살펴보겠습니다.
표본 크기를 계산하는 방법
평균을 추정하기 위해 필요한 표본 크기는 Z α/2 의 제곱에 표준 편차(σ)를 곱하고 원하는 오차 한계(e)로 나눈 값과 같습니다. 따라서 표본 크기를 계산하는 공식은 다음과 같습니다.
![]()
금:
-

표본 크기입니다.
-
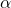
원하는 유의 수준입니다. 이를 고려하여
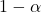
원하는 신뢰 수준입니다.
-

는 α/2의 확률에 해당하는 표준 정규 분포의 분위수입니다. 표본 크기가 크고 95% 신뢰 수준의 경우 일반적으로 1.96에 가깝고 99% 신뢰 수준의 경우 일반적으로 2.576에 가깝습니다.
-

표준편차입니다.
이 공식에서는 인구 규모가 무한하다고 가정합니다. 즉, 인구 규모가 매우 크거나 알 수 없다는 뜻입니다.
참고: 위 공식은 평균에 대한 신뢰 공식 구간 에서 파생되었습니다.
표본 크기 계산의 예
이 섹션에서는 통계 조사에 적합한 표본 크기를 예로 계산해 보겠습니다.
- 모집단의 표준편차가 15 정도인 것은 알지만 그 평균을 모르기 때문에 평균을 추정하는 연구를 진행하고자 합니다. 95% 신뢰 수준에서 ±2의 오차 한계를 원한다면 어떤 표본 크기가 필요합니까?
위에서 본 것처럼 표본 크기를 계산하는 공식은 다음과 같습니다.
![]()
이 경우 원하는 신뢰 수준은 95%이므로 해당 Z α/2 값은 1.96입니다.
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-54dda39d0da5b29f2d25728b89565859_l3.png)
마지막으로 이제 모든 매개변수의 가치가 얼마인지 알았으므로 해당 값을 공식에 대입하고 표본 크기를 계산합니다.
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle n&=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2\\[2ex] n&=\left(\frac{1,96\cdot 15}{2}\right)^2\\[2ex] n&=216,09 \approx 217 \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-dd8e2d30042f759051fb52c5c55ade44_l3.png)
간단히 말해서, 원하는 요구 사항을 충족하는 모집단 평균을 추정하려면 최소한 217명의 개인 표본이 필요합니다.
표본 크기, 신뢰 수준 및 오차 한계
필요한 신뢰 수준과 오차 한계에 따라 필요한 표본 크기가 달라집니다. 따라서 표본 크기, 신뢰 수준 및 오차 한계는 다음과 같은 관계가 있습니다.
- 표본 크기와 신뢰 수준은 정비례합니다. 즉, 신뢰 수준이 증가하면 표본 크기도 증가합니다.
- 표본 크기와 오차 한계는 반비례합니다. 따라서 오차 한계가 증가하면 표본 크기가 감소합니다.
- 따라서 표본 크기를 늘리면 신뢰 수준이 높아지거나 오차 한계가 줄어들 수 있습니다.
기타 표본 크기 공식
추정할 모수에 따라 필요한 표본 크기에 대한 공식이 약간 다릅니다. 따라서 이 섹션에서는 일부 특수한 경우에 표본 크기를 계산하는 데 유용할 수 있는 다른 공식을 살펴보겠습니다.
비율의 표본 크기
비율(p)을 추정하는 데 필요한 표본 크기를 계산하는 공식은 다음과 같습니다.
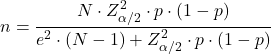
확률의 표본 크기
확률을 추정하려면 다음 공식을 사용하여 필요한 표본 크기를 결정하는 것이 좋습니다.
![]()
두 개의 독립 평균을 비교하기 위한 표본 크기
주어진 α 위험과 β 위험을 사용하여 두 개의 독립 평균을 비교할 때 표본 크기를 계산하는 공식은 다음과 같습니다.
![]()
금
![]()
대립 가설의 두 평균 사이의 차이입니다.
두 쌍의 평균을 비교하기 위한 표본 크기
고정 오차 α 및 오차 β를 사용하여 두 쌍의 평균을 비교하려는 경우 표본의 관측치 수를 찾는 데 사용하는 공식은 다음과 같습니다.
![]()
금
![]()
대립 가설의 두 쌍 평균 간의 차이입니다.
![]()
이는 동일한 개인에 대한 두 측정값 간의 차이의 분산입니다.