표준편차가 왜 중요한가요? (설명 + 예)

표준편차는 표본의 값 분포를 측정하는 데 사용됩니다.

다음 공식을 사용하여 주어진 표본의 표준 편차를 계산할 수 있습니다.

√ Σ(x _i – x _bar ) ² / (n-1)

금:

• Σ: 합계를 의미하는 기호
• x _i : 샘플의 ^i번째 값
• x _bar : 샘플 평균
• n: 표본 크기

표준 편차 값이 높을수록 값이 샘플에 더 많이 분산되어 있습니다. 반대로, 표준편차 값이 낮을수록 값이 더 밀접하게 클러스터링됩니다.

학생들이 자주 묻는 질문은 표준편차가 왜 중요한가입니다.

대답: 표준 편차는 주어진 데이터 세트의 값 분포를 알려주기 때문에 중요합니다.

우리는 데이터 세트를 분석할 때마다 다음 측정항목을 찾고 싶습니다.

• 데이터세트의 중심입니다 . “중심”을 측정하는 가장 일반적인 방법은 평균과 중앙값을 사용하는 것입니다.
• 데이터 세트의 값 분포 . 스프레드를 측정하는 가장 일반적인 방법은 표준편차를 사용하는 것입니다.

중심이 어디에 있는지, 값의 분포가 무엇인지 알면 어떤 데이터 세트에서도 값의 분포를 잘 이해할 수 있습니다.

다음 예에서는 실제로 표준 편차의 중요성을 보여줍니다.

예시 1: 급여 분배

회사 A의 평균 급여가 $80,000이고 표준 편차가 $20,000라고 가정합니다. 표준편차가 너무 크기 때문에 이 회사에 근무한다고 해서 연봉이 80,000달러에 가깝게 지급된다는 보장은 없습니다. 왜냐하면 급여에 차이가 있기 때문입니다.

반대로 B회사의 평균 급여도 $80,000이지만 표준편차는 $4,000에 불과하다고 가정해 보겠습니다. 이 표준 편차는 매우 작기 때문에 급여 변동이 거의 없기 때문에 $80,000에 가까운 급여를 받을 것이라고 확신할 수 있습니다.

이 두 회사의 급여 분포를 시각화하기 위해 상자 그림을 만든 경우 다음과 같을 수 있습니다.

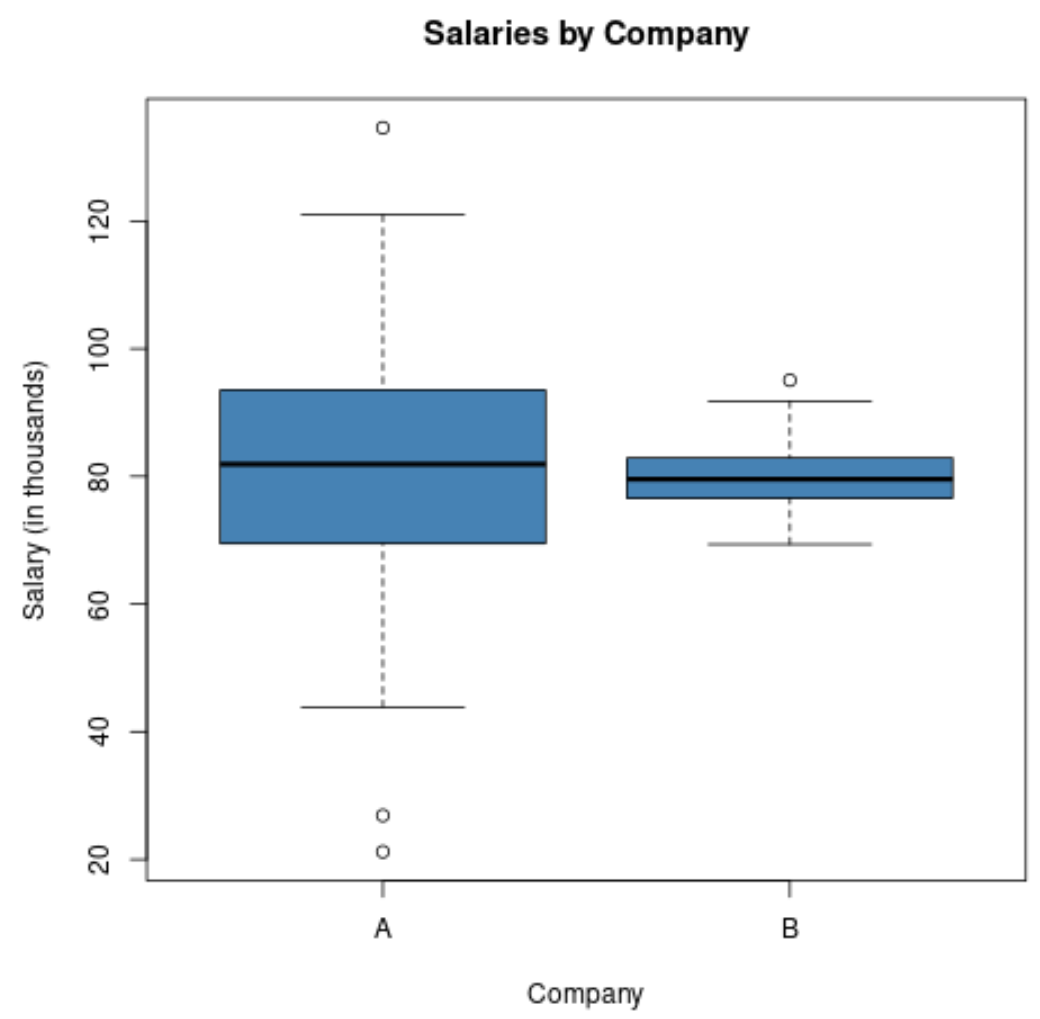
임금의 표준편차가 훨씬 높을수록 회사 A의 상자 그림 길이가 더 길다는 점에 유의하세요.

두 회사의 평균 연봉은 동일하지만 A회사의 연봉 격차가 훨씬 더 컸습니다.

사례 2: 주택 가격 분포

A 동네의 평균 주택 가격이 $250,000이고 표준 편차가 $50,000라고 가정합니다. 표준편차가 상당히 크기 때문에 이는 일부 주택 가격이 $250,000보다 훨씬 높을 수도 있고 다른 주택 가격이 훨씬 낮을 수도 있음을 의미합니다. 이 동네의 특정 주택을 살펴보면 가격이 평균에 가까울 것이라는 보장은 없습니다.

반대로 B 동네의 평균 주택 가격도 $250,000이지만 표준 편차는 $10,000에 불과하다고 가정합니다. 이 표준 편차는 매우 작기 때문에 인근에서 보는 모든 주택이 이 가격에 마감될 가능성이 높다고 확신할 수 있습니다.

이 두 동네의 주택 가격 분포를 시각화하기 위해 상자 그림을 만든 경우 다음과 같을 수 있습니다.

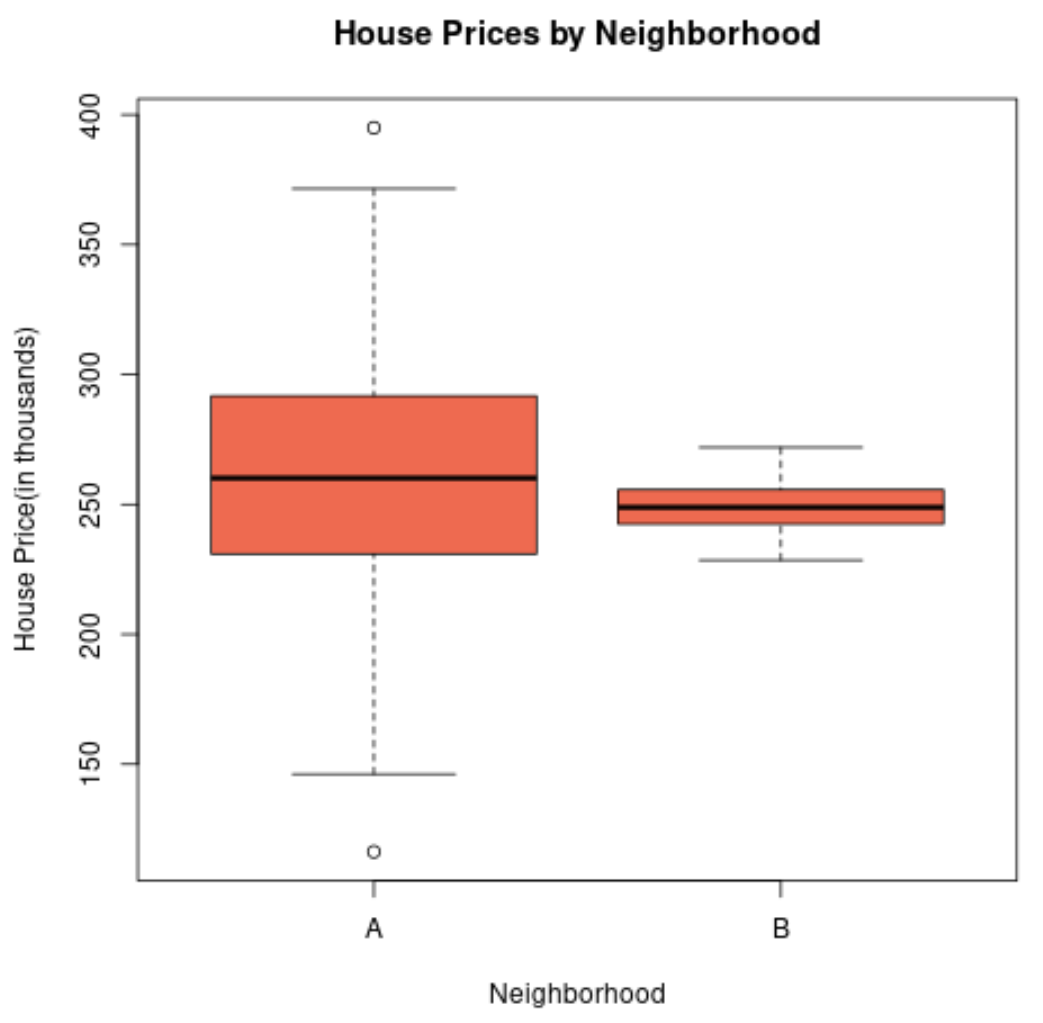
부동산 가격의 표준편차가 훨씬 높을수록 동네 A의 상자 그림 길이가 더 길어집니다.

실제로 주택 가격은 A 동네의 경우 $150,000 미만에서 $400,000 이상인 반면, B 동네의 경우 가격은 약 $230,000~$270,000에 불과합니다.

동네별 집값의 표준편차만 알면 동네별 집값 변동폭이 얼마나 될지 알 수 있다.

추가 리소스

좋은 표준편차로 간주되는 것은 무엇입니까?
범위 대 표준편차: 각각을 사용해야 하는 경우
변동계수 대 표준편차: 차이