피어슨 상관 계수
이 기사에서는 피어슨 상관 계수(또는 선형 상관 계수)가 무엇인지, 그리고 어떤 용도로 사용되는지 설명합니다. 단계별 연습을 통해 Pearson 상관 계수를 계산하는 방법을 알아봅니다. 또한 마지막에 있는 온라인 계산기를 사용하여 모든 데이터 세트의 Pearson 상관 계수 값을 찾을 수 있습니다.
피어슨의 상관계수는 무엇입니까?
선형 상관 계수 또는 간단히 상관 계수 라고도 하는 피어슨 상관 계수는 두 변수 간의 관계를 나타내는 통계적 척도입니다.
두 변수 사이의 피어슨 상관 계수를 계산하려면 해당 변수의 공분산을 분산 곱의 제곱근으로 나누어야 합니다.
따라서 Pearson 상관 계수는 두 정량적 확률 변수 사이의 선형 의존성을 수량화하려고 시도합니다. 선험적으로, 변수 사이의 상관관계를 수치적으로 평가하는 것은 복잡합니다. 왜냐하면 pue에서와 같이 Pearson 상관 계수의 목적이 변수 사이의 관계를 평가하는 것이라면 변수 쌍이 더 많은 상관관계가 있는지 결정하기 어렵기 때문입니다. 그들 사이를 비교하십시오.
피어슨 상관 지수의 값은 -1에서 +1 사이입니다. 피어슨 상관 계수의 값이 어떻게 해석되는지 아래에서 살펴보겠습니다.
피어슨 상관 계수 공식
두 통계 변수의 피어슨 상관 계수는 변수의 공분산과 각 변수의 분산 곱의 제곱근 사이의 몫과 같습니다.
따라서 피어슨 상관 계수를 계산하는 공식은 다음과 같습니다.
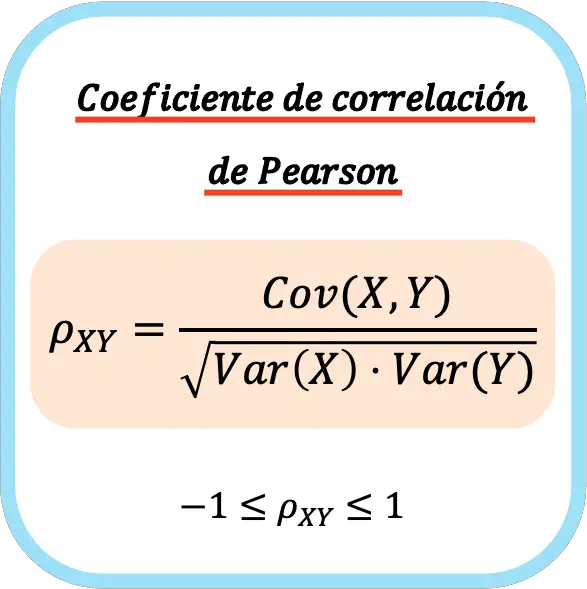
👉 아래 계산기를 사용하여 모든 데이터 세트에 대한 Pearson 상관 계수를 계산할 수 있습니다.
피어슨 상관 계수는 모집단에 대해 계산될 때 일반적으로 그리스 문자 ρ로 표시됩니다. 그러나 표본을 기준으로 계수를 계산할 때 문자 r은 일반적으로 기호로 사용됩니다.
Pearson 상관 계수를 결정하려면 두 변수 간의 공분산과 변수의 분산을 계산하는 방법을 아는 것이 중요합니다. 또한 이러한 통계적 측정값이 무엇을 의미하는지 이해해야 합니다. 따라서 설명을 계속하기 전에 다음 두 기사를 읽는 것이 좋습니다.
피어슨 상관 계수 계산의 예
피어슨 상관계수의 정의와 그 공식을 고려하면, 아래의 단계별 예시를 통해 어떻게 계산되는지 확인할 수 있습니다.
- 다음 두 연속 변수 간의 Pearson 상관 계수를 계산합니다.

Pearson 상관 계수를 계산하기 전에 데이터 세트를 산점도로 표현하여 두 변수 간의 관계를 분석합니다.
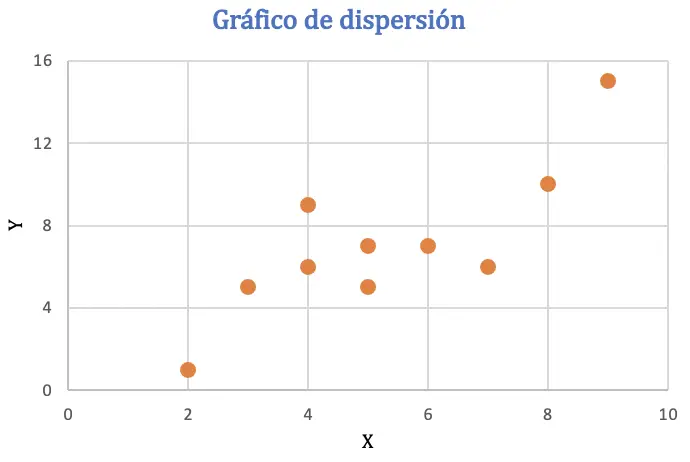
산점도를 통해 데이터가 긍정적인 추세를 가질 수 있다는 것을 추론할 수 있습니다. 즉, 한 변수의 값이 증가하면 다른 변수도 증가한다는 것을 알 수 있습니다. 상관관계를 확인하기 위해 Pearson 계수를 찾습니다.
가장 먼저 해야 할 일은 각 변수의 산술 평균을 개별적으로 찾는 것입니다. 이는 데이터의 총합을 관측치 수로 나눈 것과 같습니다.
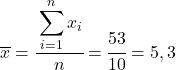
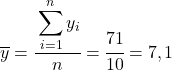
이제 각 변수의 평균을 알았으므로 데이터 테이블에 다음 열을 추가해야 합니다.
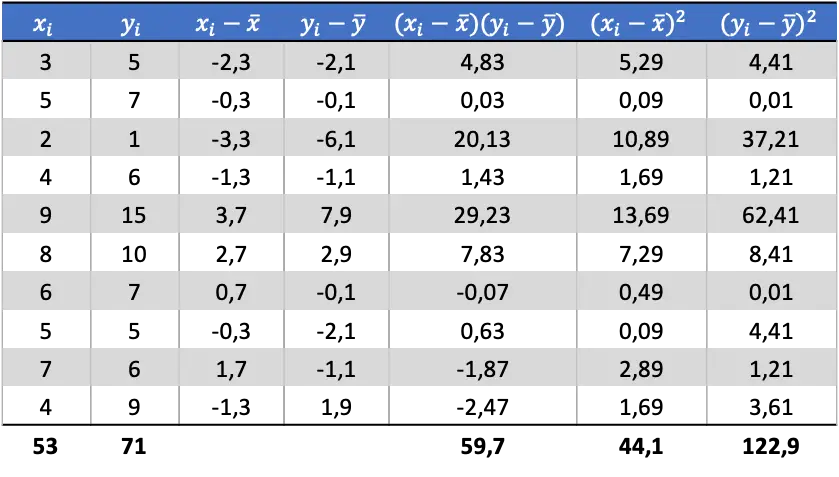
표의 계산된 데이터에서 공분산과 분산의 값을 결정합니다(이 작업이 어떻게 수행되었는지 기억하지 못하는 경우 위에 자세히 설명된 두 개의 링크가 있습니다).
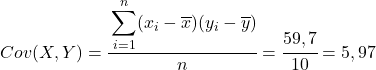
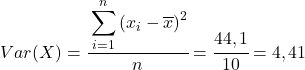
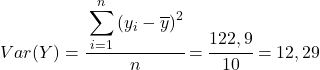
마지막으로 간단히 Pearson 상관 계수 공식을 적용하여 해당 값을 구합니다.
![]()
피어슨 상관계수는 1에 매우 가까운 값을 가지며, 이는 두 변수가 상당히 강한 양의 상관관계를 가지고 있음을 의미합니다.
보시다시피 Pearson 상관 계수를 결정하려면 Excel과 같은 프로그램을 사용하여 열 계산을 더 빠르게 수행하는 것이 매우 유용합니다.
피어슨 상관 계수 계산기
두 변수 사이의 피어슨 상관 계수를 계산하려면 다음 계산기에 일련의 통계 데이터를 입력하십시오. 첫 번째 상자에는 한 변수의 값만 있고 두 번째 상자에는 두 번째 변수의 값만 있도록 데이터 쌍을 분리해야 합니다.
데이터는 공백으로 구분해야 하며 소수점 구분 기호로 마침표를 사용하여 입력해야 합니다.
피어슨 상관 계수 해석
이 섹션에서는 피어슨 상관 계수를 해석하는 방법을 살펴보겠습니다. 왜냐하면 그 값을 아는 것만으로는 충분하지 않지만 그 의미를 분석하는 방법을 알아야 하기 때문입니다.
따라서 Pearson 상관 계수의 해석은 해당 값에 따라 달라집니다.
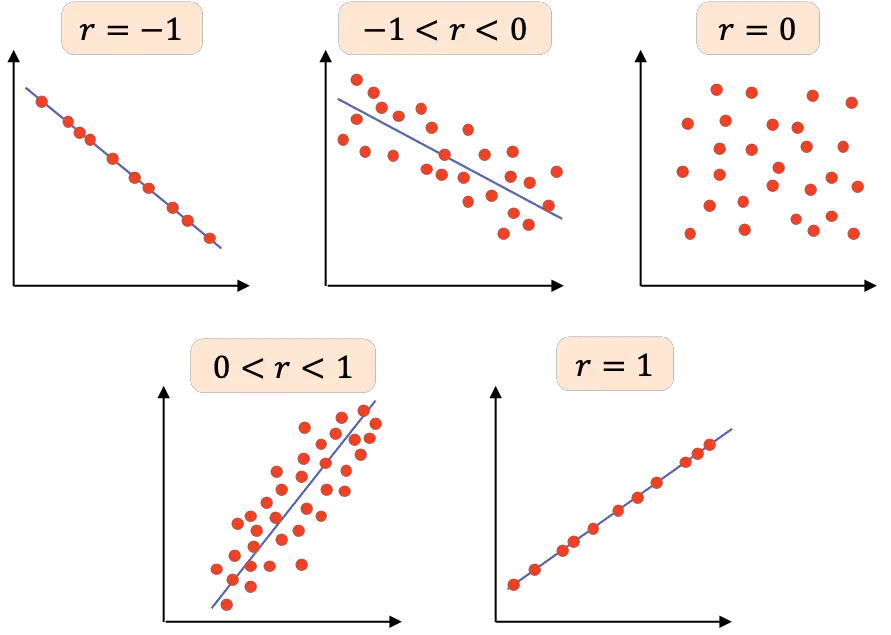
- r=-1 : 두 변수는 완벽한 음의 상관관계를 가지므로 모든 점이 연결되는 음의 기울기를 갖는 선을 그릴 수 있습니다.
- -1<r<0 : 두 변수 사이의 상관관계는 음수이므로 한 변수가 증가하면 다른 변수는 감소합니다. 값이 -1에 가까울수록 변수와 음의 관련성이 더 높습니다.
- r=0 : 두 변수 사이의 상관관계가 매우 약합니다. 실제로 두 변수 사이의 선형 관계는 0입니다. 이는 변수가 비선형 관계를 가질 수 있으므로 변수가 독립적이라는 의미는 아닙니다.
- 0<r<1 : 두 변수 사이의 상관관계는 양수이며, 값이 +1에 가까울수록 변수 사이의 관계가 더 강합니다. 이 경우 한 변수의 값이 증가하면 다른 변수의 값도 증가하는 경향이 있습니다.
- r=1 : 두 변수는 완벽한 양의 상관 관계를 갖습니다. 즉, 양의 선형 관계를 갖습니다.
요약하면 다음 표에는 Pearson 상관 계수에 대한 다양한 해석이 나와 있습니다.
| 값 | 해석 |
|---|---|
| r=-1 | 완벽한 음의 상관관계. |
| -1<r<0 | 음의 상관관계: 상관관계가 -1에 가까울수록 강한 상관관계입니다. |
| r=0 | 선형 상관관계가 없습니다. |
| 0<r<1 | 양의 상관관계: 상관관계가 +1에 가까울수록 더 강합니다. |
| r=1 | 완벽한 양의 상관관계. |
두 변수 사이에 관계가 있다고 해서 두 변수 사이에 인과관계가 있다는 의미는 아닙니다 . 즉, 두 변수 사이의 상관관계가 변수의 변화가 변수 변화의 원인이라는 의미는 아닙니다. 다른 변수.
예를 들어, 체내에서 서로 다른 두 가지 호르몬의 생산 사이에 긍정적인 관계가 있다는 것을 알게 된다면, 한 호르몬의 증가가 다른 호르몬의 증가로 이어질 필요는 없습니다. 신체는 질병과 싸우기 위해 두 호르몬이 모두 필요하고 동시에 두 호르몬의 수준을 증가시키기 때문에 두 호르몬을 모두 생성할 수 있으며, 이 경우 원인은 질병이 될 수 있습니다. 두 호르몬 사이에 인과관계가 있는지 확인하려면 추가 연구가 수행되어야 합니다.