ကြိမ်နှုန်းဖြန့်ဖြူးခြင်း။

ဤဆောင်းပါးတွင် ကြိမ်နှုန်းခွဲဝေမှုများသည် မည်ကဲ့သို့ အောင်မြင်ကြောင်းကို ရှင်းပြထားသည်။ ကြိမ်နှုန်းခွဲဝေမှု၏ အဆင့်ဆင့်သော ဥပမာများကိုလည်း သင်တွေ့နိုင်မည်ဖြစ်ပြီး၊ ထို့အပြင် ဖြေရှင်းနိုင်သော လေ့ကျင့်ခန်းများဖြင့် လေ့ကျင့်နိုင်မည်ဖြစ်သည်။

ကြိမ်နှုန်းဖြန့်ဝေခြင်းဆိုသည်မှာ အဘယ်နည်း။

စာရင်းဇယားများတွင်၊ ကြိမ်နှုန်းဖြန့်ဝေမှုသည် နမူနာတစ်ခု၏ မတူညီသောတန်ဖိုးများကို အတန်းများအဖြစ် အုပ်စုဖွဲ့ပြီး ကော်လံတစ်ခုစီတွင် တန်ဖိုးတစ်ခုစီ၏ ကြိမ်နှုန်းအမျိုးအစားကို ပြသသည့်ဇယားတစ်ခုဖြစ်သည်။ ထို့ကြောင့်၊ ဒေတာအစုတစ်ခုတွင် ကြိမ်နှုန်းအမျိုးအစားအားလုံးကိုပြသရန် ကြိမ်နှုန်းဖြန့်ဝေခြင်းကို အသုံးပြုသည်။

အထူးသဖြင့်၊ ကြိမ်နှုန်းခွဲဝေမှုတွင် ပကတိကြိမ်နှုန်း၊ စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်း၊ နှိုင်းယှဥ်ကြိမ်နှုန်းနှင့် တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းတို့ ပါဝင်သည်။

ကြိမ်နှုန်းခွဲဝေမှု၏ ဝိသေသများထဲမှ တစ်ခုမှာ ကိန်းဂဏန်းကိန်းရှင်တစ်ခု၏ ကိန်းဂဏန်းကိန်းရှင်နမူနာကို အကျဉ်းချုပ်ဖော်ပြခြင်းအတွက် ၎င်းတို့သည် အလွန်အသုံးဝင်ပါသည်။

ကြိမ်နှုန်းဖြန့်ဝေနည်း

ကြိမ်နှုန်းခွဲဝေမှုကို လုပ်ဆောင်ရန်၊ သင်သည် အောက်ပါအဆင့်များကို လိုက်နာရပါမည်။

1. ဒေတာကို မတူညီသော အမျိုးအစားများအဖြစ် စုစည်းပြီး အတန်းတစ်ခုစီသည် အမျိုးအစားတစ်ခုနှင့် ကိုက်ညီသည့် ဇယားတစ်ခုကို ဖန်တီးပါ။
2. ဇယား၏ဒုတိယကော်လံရှိ အမျိုးအစားတစ်ခုစီ၏ ပကတိအကြိမ်ရေကို တွက်ချက်ပါ။
3. ဇယား၏တတိယကော်လံတွင် အမျိုးအစားတစ်ခုစီ၏ စုစည်းမှု ပကတိအကြိမ်ရေကို တွက်ချက်ပါ။
4. ဇယား၏ စတုတ္ထကော်လံရှိ အမျိုးအစားတစ်ခုစီ၏ နှိုင်းရကြိမ်နှုန်းကို တွက်ချက်ပါ။
5. ဇယား၏ ပဉ္စမကော်လံတွင် အမျိုးအစားတစ်ခုစီ၏ တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းကို တွက်ချက်ပါ။
6. ရွေးချယ်နိုင်သောအားဖြင့်၊ ဆွေမျိုးကြိမ်နှုန်းနှင့် တိုးပွားလာသော ဆွေမျိုးကြိမ်နှုန်းကို ရာခိုင်နှုန်းအဖြစ် တွက်ချက်ထားသည့်အတွက် ကော်လံနှစ်ခုလုံးကို ပေါင်းထည့်နိုင်သည်၊ ၎င်းအတွက် သင်သည် ကော်လံနှစ်ခုလုံးကို 100 ဖြင့် မြှောက်ရန် လိုအပ်သည်။

ကြိမ်နှုန်းဖြန့်ဝေမှု ဥပမာ

ကြိမ်နှုန်းခွဲဝေမှု၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ၎င်းကိုတည်ဆောက်ပုံသီအိုရီကို ကျွန်ုပ်တို့တွေ့မြင်ပြီးသည်နှင့်၊ ဤအပိုင်းတွင် နမူနာတစ်ခုကို အဆင့်ဆင့်ဖြေရှင်းထားသည်။

• ကျောင်းသား 30 ရှိသော အတန်းတစ်တန်းတွင် စာရင်းအင်းဘာသာရပ်တွင် ရရှိသော အမှတ်များမှာ အောက်ပါအတိုင်းဖြစ်သည်။ ဒေတာအတွဲ၏ ကြိမ်နှုန်းခွဲဝေမှုကို တည်ဆောက်ပါ။

ဂဏန်းများအားလုံးသည် ကိန်းပြည့်များသာဖြစ်နိုင်သောကြောင့် ၎င်းသည် သီးခြားကွဲလွဲချက်ဖြစ်သည်။ ထို့ကြောင့် အချက်အလက်များကို ကြားကာလအဖြစ် အုပ်စုဖွဲ့ရန် မလိုအပ်ပါ။

ထို့ကြောင့်၊ ကြိမ်နှုန်းခွဲဝေမှုတစ်ခုပြုလုပ်ရန်၊ မတူညီသောတန်ဖိုးတစ်ခုစီသည် အတန်းတစ်ခုဖြစ်လာမည့် ဇယားတစ်ခုတည်ဆောက်ရန် လိုအပ်ပြီး၊ ထို့နောက် တန်ဖိုးတစ်ခုစီ၏ ပကတိအကြိမ်ရေကို ရှာဖွေရန် လိုအပ်ပါသည်။

absolute frequencies အားလုံး၏ပေါင်းလဒ်သည် ဒေတာစုစုပေါင်းအရေအတွက်နှင့် ညီမျှကြောင်း သတိပြုပါ။ ဤစည်းမျဉ်းကို မလေးစားပါက၊ သင်သည် အချို့သော အချက်အလက်များကို ပေးဆောင်ရန် မေ့သွားသည်ဟု ဆိုလိုသည်။

ယခု ကျွန်ုပ်တို့သည် absolute frequency ကို သိရှိပြီး၊ စုစည်းမှု absolute frequency ကို တွက်ချက်ရန် လိုအပ်ပါသည်။ ဤတွက်ချက်မှုအတွက် ကျွန်ုပ်တို့တွင် ရွေးချယ်စရာနှစ်ခုရှိသည်- ကျွန်ုပ်တို့သည် တန်ဖိုး၏ ပကတိကြိမ်နှုန်းနှင့် အသေးငယ်ဆုံးတန်ဖိုးများ၏ ပကတိကြိမ်နှုန်းအားလုံးကို ပေါင်းထည့်ခြင်း သို့မဟုတ် ဆန့်ကျင်ဘက်အနေနှင့်၊ ကျွန်ုပ်တို့သည် တန်ဖိုး၏ ပကတိကြိမ်နှုန်းနှင့် ယခင်တန်ဖိုး၏ ပကတိအကြိမ်ရေကို ပေါင်းထည့်ပါသည်။

နောက်ဆုံးတန်ဖိုး၏ စုစည်းမှု ပကတိအကြိမ်ရေသည် ဒေတာစုစုပေါင်းအရေအတွက်နှင့် အမြဲသက်ဆိုင်သည်၊ တွက်ချက်မှုများမှန်ကန်ကြောင်း အတည်ပြုရန် ဤလှည့်ကွက်ကို အသုံးပြုနိုင်သည်။

ထို့နောက်၊ ကျွန်ုပ်တို့သည် စုစုပေါင်းဒေတာအမှတ် (30) ဖြင့် ပကတိကြိမ်နှုန်းကို ပိုင်းခြားတွက်ချက်ထားသည့် နှိုင်းရကြိမ်နှုန်းကို ဆုံးဖြတ်ရန် လိုအပ်ပါသည်။

နှိုင်းရကြိမ်နှုန်းအားလုံး၏ ပေါင်းလဒ်သည် 1 နှင့် အမြဲညီမျှကြောင်း မှတ်သားထားပါ၊ သို့မဟုတ်ပါက ကြိမ်နှုန်းဖြန့်ဝေမှု၏ အချို့သော တွက်ချက်မှုမှာ မှားယွင်းနေသည်ဟု မှတ်သားထားပါ။

နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းကို ထုတ်ယူရန်သာ လိုအပ်သည်။ ၎င်းကိုလုပ်ဆောင်ရန်၊ သင်သည် မေးခွန်းရှိတန်ဖိုး၏ နှိုင်းရကြိမ်နှုန်းနှင့် ယခင်နှိုင်းရကြိမ်နှုန်းများအားလုံးကို ပေါင်းထည့်ရမည်ဖြစ်ပြီး၊ သို့မဟုတ် တူညီသောပမာဏဖြစ်သည့် ယခင်စုဆောင်းထားသော ဆွေမျိုးကြိမ်နှုန်းကို ပေါင်းထည့်ရမည်-

အတိုချုပ်အားဖြင့်၊ ပြဿနာဒေတာ၏ ကြိမ်နှုန်းအားလုံးနှင့် ကြိမ်နှုန်းဖြန့်ဝေမှုသည် အောက်ပါအတိုင်းဖြစ်သည်။

အုပ်စုလိုက်ဒေတာအတွက် ကြိမ်နှုန်းဖြန့်ဝေခြင်း။

ဒေတာအတွက် ကြိမ်နှုန်းခွဲဝေမှု တစ်ခု ပြုလုပ်ရန် တစ်ခုတည်းသော ခြားနားချက်မှာ ဒေတာအစုံကို မတူညီသော ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ရမည်ဖြစ်သော်လည်း ကျန်တွက်ချက်မှုများကို ဒေတာအုပ်စုမဖွဲ့ဘဲ ကြိမ်နှုန်းခွဲဝေမှုတွင် အတူတူပင်ဖြစ်ပါသည်။

ဥပမာအနေဖြင့်၊ အုပ်စုဖွဲ့ဒေတာအတွက် ကြိမ်နှုန်းခွဲဝေမှုကို တည်ဆောက်ခြင်းဆိုင်ရာ ပြဿနာကို အောက်တွင် ဖြေရှင်းထားသည်။

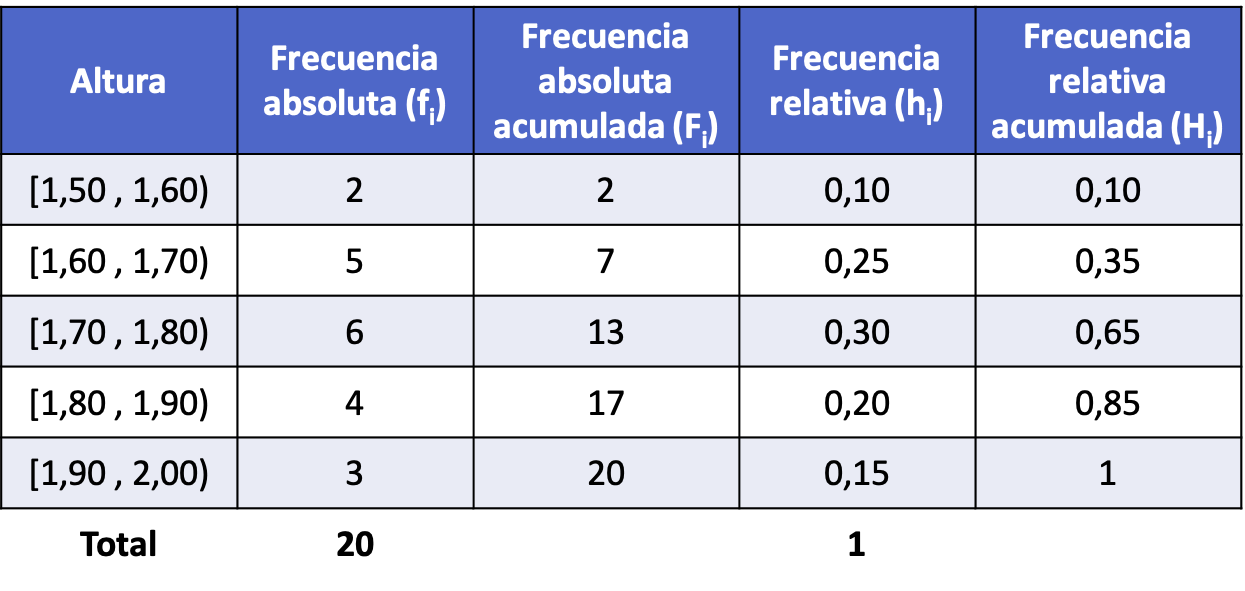
• လူ 20 ၏အမြင့်ကိုတိုင်းတာခဲ့ပြီးအောက်ပါရလဒ်များကိုရရှိခဲ့သည်။ ဒေတာများကို ကြားကာလများအဖြစ် ပိုင်းခြားခြင်းဖြင့် ကြိမ်နှုန်းခွဲဝေမှုကို ဖန်တီးပါ။

ဤနမူနာရှိ ဒေတာသည် ကိန်းဂဏာန်းများသည် ဒဿမဖြစ်နိုင်ပြီး မည်သည့်တန်ဖိုးကိုမဆို ယူနိုင်သောကြောင့် ဆက်တိုက်ဖြန့်ဝေမှုနောက်လိုက်ပါသည်။ ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် ဒေတာကို ကြားကာလများအဖြစ် အုပ်စုဖွဲ့သည့် ကြိမ်နှုန်းခွဲဝေမှုကို ပြုလုပ်မည်ဖြစ်သည်။

နမူနာတစ်ခု၏ကြားကာလများကိုဖန်တီးရန် သင်္ချာစည်းမျဉ်းများစွာရှိသော်လည်း ဤအခြေအနေတွင် ကျွန်ုပ်တို့သည် အကျယ် 10 ဒသမ နှင့် ကြားကာလများကို ရိုးရိုးရှင်းရှင်းဖန်တီးပါမည်။

ထို့ကြောင့်၊ ကြားကာလတစ်ခုစီအတွက် ကြိမ်နှုန်းအမျိုးအစားအားလုံးကို တွက်ချက်ပြီးနောက် (လုပ်ထုံးလုပ်နည်းသည် အထက်ဖော်ပြပါ ဥပမာတွင် အတူတူပင်ဖြစ်သည်)၊ ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ထားသော ဒေတာနှင့်အတူ ကြိမ်နှုန်းဖြန့်ဝေမှုသည် အောက်ပါအတိုင်းဖြစ်သည်-

ကြွပ်ကြွပ်အိတ် ကြိမ်နှုန်းဖြန့်ဖြူးရေး လေ့ကျင့်ခန်း

လေ့ကျင့်ခန်း ၁

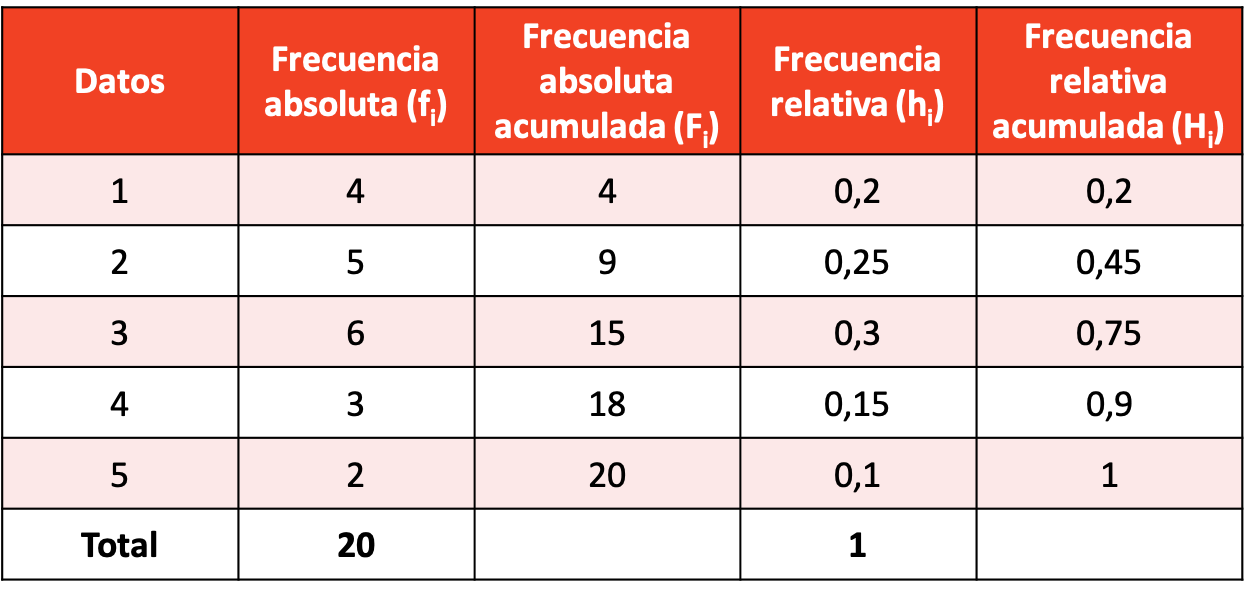
တစ်လလျှင် ရုပ်ရှင်ရုံသို့ အကြိမ်ရေ မည်မျှသွားသည်ကို လူ 20 ကို ကျွန်ုပ်တို့မေးခဲ့ပြီး ရလဒ်များမှာ အောက်ပါအတိုင်းဖြစ်သည်။

ရရှိလာသောဒေတာနမူနာဖြင့် ကြိမ်နှုန်းခွဲဝေမှုကို ပြုလုပ်ပါ။

ကြိမ်နှုန်းအမျိုးအစားအားလုံး၏ တွက်ချက်မှုဖြင့် ကြိမ်နှုန်းဖြန့်ဝေမှုသည် အောက်ပါအတိုင်းဖြစ်သည်။

လေ့ကျင့်ခန်း ၂

ဝန်ထမ်း ၃၆ ဦးရှိသော ကုမ္ပဏီတစ်ခုရှိ အလုပ်သမားများ၏ အလေးချိန်ဆိုင်ရာ ကိန်းဂဏန်းလေ့လာမှုကို သင်လုပ်ဆောင်လိုပါသည်။ ဤသည်မှာ ကီလိုဂရမ်ဖြင့် ဖော်ပြထားသော အလုပ်သမားများ၏ အလေးချိန်များဖြစ်သည်။

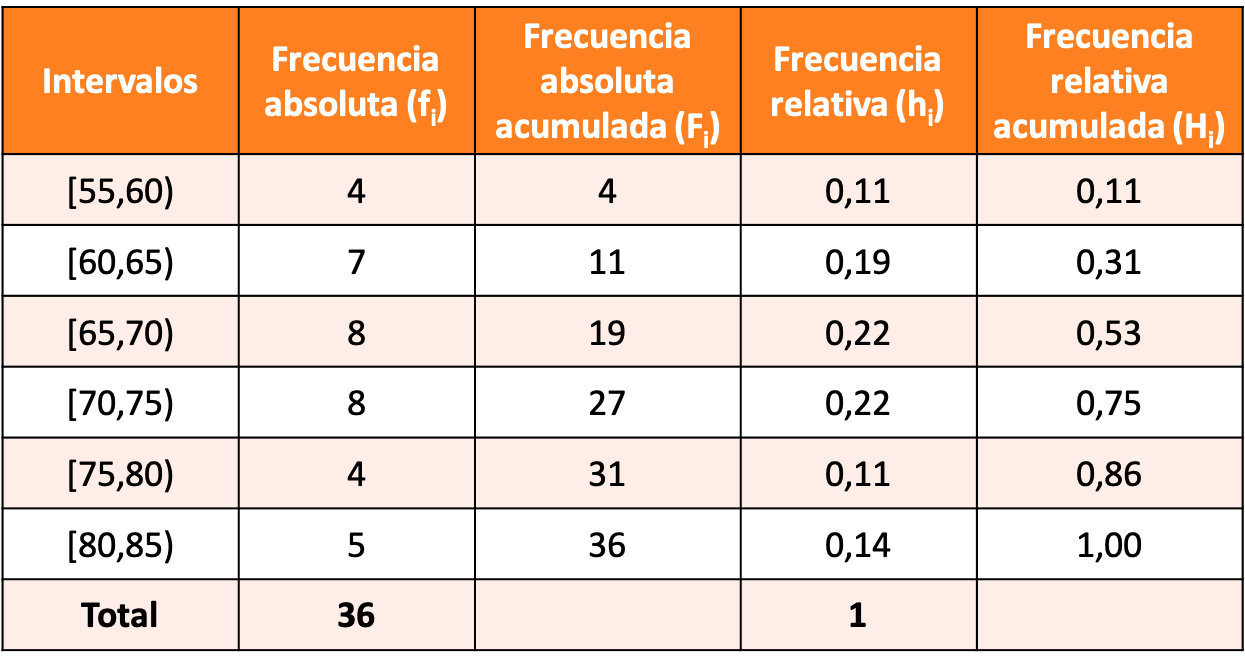
5 ယူနစ်များကြားကာလများပြုလုပ်ခြင်းဖြင့် အုပ်စုဖွဲ့ဒေတာဖြင့် ကြိမ်နှုန်းခွဲဝေမှုတစ်ခုကို တည်ဆောက်ပြီး ပထမကြားကာလသည် [55,60) ဖြစ်ပါစေ။

လေ့ကျင့်ခန်းအတွက် ဖြေရှင်းချက်မှာ အောက်ပါ အကြိမ်ရေ ဖြန့်ဝေမှု ဖြစ်ပါသည်။