ချီစတုရန်းဖြန့်ချီရေးဇယားကို ဘယ်လိုဖတ်မလဲ။

ဤသင်ခန်းစာတွင် Chi-square ဖြန့်ချီရေးဇယားကို ဖတ်ရှုပြီး အဓိပ္ပာယ်ပြန်ဆိုပုံကို ရှင်းပြထားသည်။

ချီစတုရန်း ဖြန့်ချီရေးဇယားက ဘာလဲ။

Chi-square ဖြန့်ချီရေးဇယား သည် Chi-square ဖြန့်ဖြူးမှု၏ အရေးပါသောတန်ဖိုးများကို ပြသသောဇယားတစ်ခုဖြစ်သည်။ Chi-square ဖြန့်ချီရေးဇယားကို အသုံးပြုရန်၊ သင်သည် တန်ဖိုးနှစ်ခုသာ သိရန် လိုအပ်သည်-

• Chi square test အတွက် လွတ်လပ်မှုဒီဂရီ
• စမ်းသပ်မှု၏ အယ်လ်ဖာအဆင့် (အများအားဖြင့် ရွေးချယ်မှုများမှာ 0.01၊ 0.05 နှင့် 0.10)

အောက်ပါပုံသည် ဇယား၏ဘယ်ဘက်ခြမ်းတွင် လွတ်လပ်မှုဒီဂရီနှင့် ဇယားထိပ်ရှိ အယ်ဖာအဆင့်များပါရှိသော Chi-square ဖြန့်ချီရေးဇယား၏ ပထမတန်း 20 တန်းကို ပြသသည်-

မှတ်ချက်- လွတ်လပ်မှု ပိုဒီဂရီများပါရှိသော Chi-square ဖြန့်ချီရေးဇယား အပြည့်အစုံကို ဤနေရာတွင် ရှာနိုင်သည်။

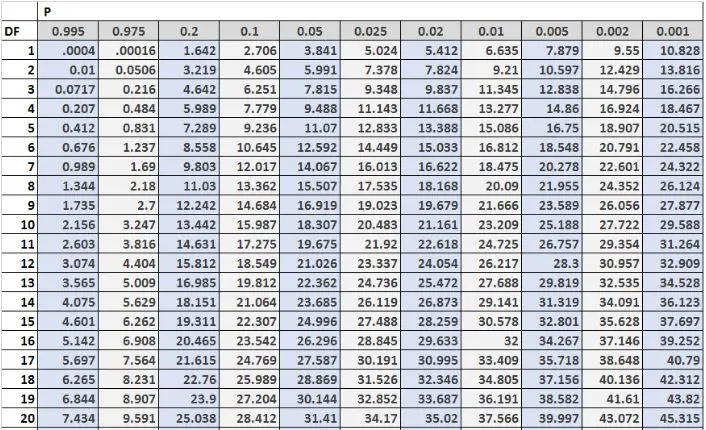
ဇယားရှိ အရေးပါသောတန်ဖိုးများကို Chi-square စမ်းသပ်မှုတစ်ခု၏ စမ်းသပ်စာရင်းဇယားများနှင့် နှိုင်းယှဉ်လေ့ရှိသည်။ စမ်းသပ်မှုစာရင်းအင်းသည် ဇယားတွင်တွေ့ရသော အရေးပါသောတန်ဖိုးထက် ကြီးပါက၊ Chi-square စမ်းသပ်မှု၏ null hypothesis ကို ငြင်းပယ်နိုင်ပြီး စစ်ဆေးမှုရလဒ်များသည် စာရင်းအင်းအရ သိသာထင်ရှားသည်ဟု ကောက်ချက်ချနိုင်သည်။

chi-square ဖြန့်ချီရေးဇယားကို အသုံးပြုခြင်း ဥပမာများ

အောက်ပါ Chi-square စမ်းသပ်မှု အမျိုးအစားသုံးမျိုးဖြင့် Chi-square ဖြန့်ချီရေးဇယားကို မည်သို့အသုံးပြုရမည်ကို ကျွန်ုပ်တို့ပြသပါမည်။

• လွတ်လပ်ရေးအတွက် Chi-square စမ်းသပ်မှု
• Chi-square စမ်းသပ်မှု
• Chi-square စမ်းသပ်မှု

လွတ်လပ်ရေးအတွက် Chi-square စမ်းသပ်မှု

ကျွန်ုပ်တို့သည် အမျိုးအစားခွဲကိန်းရှင်နှစ်ခုကြားတွင် သိသာထင်ရှားသော ဆက်နွယ်မှုရှိမရှိ စမ်းသပ်လိုသည့်အခါ လွတ်လပ်မှုအတွက် Chi-square စမ်းသပ်မှုကို ကျွန်ုပ်တို့ အသုံးပြုပါသည် ။

ဥပမာ- နိုင်ငံရေး ပါတီတစ်ခုအတွက် ဦးစားပေးမှုတွင် လိင်နှင့် ဆက်နွှယ်မှု ရှိ၊ မရှိ သိလိုသည်ဆိုပါစို့။ ကျွန်ုပ်တို့သည် မဲဆန္ဒရှင် ၅၀၀ ၏ ရိုးရှင်းသော ကျပန်းနမူနာကို ယူကာ ၎င်းတို့၏ နိုင်ငံရေး ပါတီကို နှစ်သက်မှုအကြောင်း မေးမြန်းပါသည်။ 0.05 ၏ အရေးပါမှုအဆင့်ကို အသုံးပြု၍ ကျားမသည် နိုင်ငံရေး ပါတီ၏ နှစ်သက်ရာနှင့် ဆက်စပ်မှုရှိမရှိ ဆုံးဖြတ်ရန် ချီစတုရန်းစစ်ဆေးမှုကို ပြုလုပ်ပါသည်။ အောက်ပါဇယားသည် စစ်တမ်း၏ရလဒ်များကို ဖော်ပြသည်။

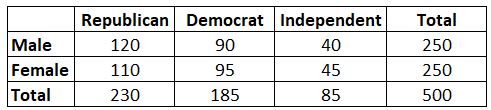
ဤ Chi-square စစ်ဆေးမှုအတွက် စစ်ဆေးမှု ကိန်းဂဏန်းသည် 0.864 ဖြစ်သည် ။

ထို့နောက် Chi square ဖြန့်ချီရေးဇယားတွင် အရေးကြီးသော စမ်းသပ်မှုတန်ဖိုးကို ကျွန်ုပ်တို့ ရှာတွေ့နိုင်ပါသည်။ လွတ်လပ်မှုဒီဂရီများသည် (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2 နှင့် တူညီပြီး ပြဿနာက 0.05 ဖြစ်သော alpha အဆင့်ကို သုံးသင့်သည်ဟု ကျွန်ုပ်တို့ကို ပြောသည်၊ Chi-square ဖြန့်ချီရေးဇယားအရ၊ စမ်းသပ်မှု၏ အရေးကြီးသောတန်ဖိုးမှာ 5.991 ဖြစ်သည်။

ကျွန်ုပ်တို့၏စမ်းသပ်မှုစာရင်းအင်းသည် ကျွန်ုပ်တို့၏အရေးကြီးသောတန်ဖိုးထက်နည်းသောကြောင့်၊ ကျွန်ုပ်တို့သည် null hypothesis ကိုငြင်းပယ်ရန်ပျက်ကွက်ပါသည်။ ဆိုလိုသည်မှာ ကျား၊မ နှင့် နိုင်ငံရေး ပါတီများ၏ နှစ်သက်ရာများကြားတွင် ဆက်စပ်မှုရှိသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထား မရှိပါ။

Chi-square စမ်းသပ်မှု

categorical variable တစ်ခုသည် hypothetical distribution ကို လိုက်နာခြင်း ရှိ၊ မရှိ စမ်းသပ်လိုသောအခါတွင် chi-square goodness-of-fit test ကို အသုံးပြုပါသည်။

ဥပမာ- စတိုးဆိုင်ပိုင်ရှင်တစ်ဦးက သူ၏စနေ၊ အမှီအခိုကင်းသော သုတေသီတစ်ဦးသည် ကျပန်း သီတင်းပတ်ကုန်တွင် စတိုးဆိုင်သို့ လာရောက်လည်ပတ်ပြီး သောကြာနေ့တွင် ဖောက်သည် ၉၁ ဦး၊ စနေနေ့တွင် ၁၀၄ ဦး၊ တနင်္ဂနွေတွင် ၆၅ ဦး တွေ့ရှိခဲ့သည်။ 0.10 ၏ အရေးပါမှုအဆင့်ကို အသုံးပြု၍ ဒေတာသည် စတိုးပိုင်ရှင်၏ တောင်းဆိုချက်နှင့် ကိုက်ညီမှုရှိမရှိ ဆုံးဖြတ်ရန် ကိုက်ညီမှုကောင်းမွန်မှုကို စစ်ဆေးရန်အတွက် chi-square စမ်းသပ်မှုကို လုပ်ဆောင်ပါသည်။

ဤကိစ္စတွင်၊ စမ်းသပ်မှုစာရင်းအင်းသည် 10,616 ဖြစ်လာသည်။

ထို့နောက် Chi square ဖြန့်ချီရေးဇယားတွင် အရေးကြီးသော စမ်းသပ်မှုတန်ဖိုးကို ကျွန်ုပ်တို့ ရှာတွေ့နိုင်ပါသည်။ လွတ်လပ်မှုဒီဂရီများသည် (#outcomes-1) = 3-1 = 2 နှင့် ညီမျှပြီး alpha အဆင့် 0.10 ကို အသုံးပြုသင့်သည်ဟု ပြဿနာက ပြောပြသည်။ ထို့ကြောင့် Chi-square ဖြန့်ချီရေးဇယားအရ၊ စမ်းသပ်မှု၏ အရေးကြီးသောတန်ဖိုးမှာ 4.605 ဖြစ်သည်။

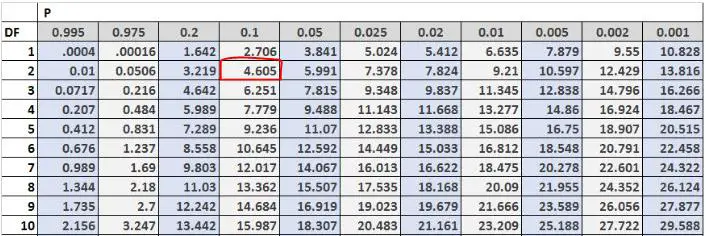
ကျွန်ုပ်တို့၏စမ်းသပ်မှုစာရင်းအင်းသည် ကျွန်ုပ်တို့၏အရေးကြီးသောတန်ဖိုးထက် ကြီးသောကြောင့်၊ ကျွန်ုပ်တို့သည် null hypothesis ကို ငြင်းပယ်ပါသည်။ ဆိုလိုသည်မှာ စနေ၊ တနင်္ဂနွေတွင် 30%၊ စနေနေ့တွင် 50% နှင့် တနင်္ဂနွေတွင် 20% နှင့် ဤစတိုးဆိုင်သို့ လာရောက်သော ဖောက်သည်များ၏ စစ်မှန်သော ဖြန့်ဖြူးမှုမှာ 30% နှင့် ညီမျှသည်ဟူ၍ ကျွန်ုပ်တို့တွင် သက်သေအလုံအလောက်ရှိသည်။

Chi-square စမ်းသပ်မှု

အုပ်စုများစွာကြားတွင် အချိုးအစားကွာခြားမှုရှိမရှိ တရားဝင်စမ်းသပ်လိုသောအခါတွင် ကျွန်ုပ်တို့သည် Chi-square စမ်းသပ်မှုကို အသုံးပြုပါသည်။

ဥပမာ- ဘတ်စကတ်ဘောလေ့ကျင့်ရေးစင်တာတစ်ခုသည် လေ့ကျင့်ရေးအစီအစဉ်အသစ်နှစ်ခုသည် ခက်ခဲသောသေနတ်ပစ်စမ်းသပ်မှုတစ်ခုအောင်မြင်ပြီးသည့် ၎င်း၏ကစားသမားအချိုးအစားကို တိုးတက်စေခြင်းရှိမရှိ ကြည့်ရှုလိုပါသည်။ ပရိုဂရမ် 1၊ 173 ပရိုဂရမ် 2 မှ ကစားသမား 172 ယောက်နှင့် လက်ရှိပရိုဂရမ်တွင် 215 ယောက်ကို ကျပန်းသတ်မှတ်ထားသည်။ လေ့ကျင့်ရေးပရိုဂရမ်များကို တစ်လကြာအသုံးပြုပြီးနောက် ကစားသမားများသည် သေနတ်ပစ်စမ်းသပ်မှုပြုလုပ်ကြသည်။ အောက်ဖော်ပြပါဇယားတွင် ၎င်းတို့အသုံးပြုခဲ့သည့် ပရိုဂရမ်အပေါ်အခြေခံ၍ သေနတ်ပစ်စမ်းသပ်မှုအောင်မြင်သည့် ကစားသမားအရေအတွက်ကို ပြသထားသည်။

0.05 ၏ အရေးပါမှုအဆင့်ကို အသုံးပြု၍ လေ့ကျင့်ရေးအစီအစဉ်တစ်ခုစီအတွက် အောင်မြင်မှုနှုန်းသည် တူညီခြင်းရှိမရှိ ဆုံးဖြတ်ရန် chi-square စမ်းသပ်မှုကို လုပ်ဆောင်ပါသည်။

ဤ Chi-square စမ်းသပ်မှုအတွက် စစ်ဆေးမှု ကိန်းဂဏန်းသည် 4.208 ဖြစ်သည် ။

ထို့နောက် Chi square ဖြန့်ချီရေးဇယားတွင် အရေးကြီးသော စမ်းသပ်မှုတန်ဖိုးကို ကျွန်ုပ်တို့ ရှာတွေ့နိုင်ပါသည်။ လွတ်လပ်မှုဒီဂရီများသည် (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2 နှင့် တူညီပြီး ပြဿနာက 0.05 ဖြစ်သော alpha အဆင့်ကို သုံးသင့်သည်ဟု ကျွန်ုပ်တို့ကို ပြောသည်၊ Chi-square ဖြန့်ချီရေးဇယားအရ၊ စမ်းသပ်မှု၏ အရေးကြီးသောတန်ဖိုးမှာ 5.991 ဖြစ်သည်။

ကျွန်ုပ်တို့၏စမ်းသပ်မှုစာရင်းအင်းသည် ကျွန်ုပ်တို့၏အရေးကြီးသောတန်ဖိုးထက်နည်းသောကြောင့်၊ ကျွန်ုပ်တို့သည် null hypothesis ကိုငြင်းပယ်ရန်ပျက်ကွက်ပါသည်။ ဆိုလိုသည်မှာ လေ့ကျင့်ရေးပရိုဂရမ်သုံးခုသည် မတူညီသောရလဒ်များထွက်ပေါ်သည်ဟုဆိုရန် လုံလောက်သော အထောက်အထားမရှိဟု ဆိုလိုပါသည်။