ဆက်စပ်မက်ထရစ်ကို ဘယ်လိုဖတ်မလဲ။
ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ ကျွန်ုပ်တို့သည် ကိန်းရှင်နှစ်ခုကြားရှိ ဆက်စပ်မှုကို နားလည်ရန် ရှာဖွေလေ့ရှိသည်။
ဥပမာအားဖြင့်၊ ကျောင်းသားတစ်ဦး၏လေ့လာမှုနာရီအရေအတွက်နှင့် စာမေးပွဲတွင် ၎င်းတို့ရရှိသည့်အဆင့်အကြား ဆက်နွယ်မှုကို ကျွန်ုပ်တို့နားလည်လိုပေမည်။
ဤဆက်နွယ်မှုကို အရေအတွက်သတ်မှတ်ရန် နည်းလမ်းတစ်ခုမှာ ကိန်းရှင်နှစ်ခုကြားရှိ မျဉ်းကြောင်းဆက်စပ်မှုကို တိုင်းတာသည့် Pearson correlation coefficient ကို အသုံးပြုခြင်းဖြစ်သည် ။ ၎င်းတွင် -1 နှင့် 1 အကြား တန်ဖိုးတစ်ခု ရှိသည်။
- -1 သည် ကိန်းရှင်နှစ်ခုကြားတွင် လုံးဝအနုတ်လက္ခဏာ မျဉ်းကြောင်းဆက်စပ်မှုကို ညွှန်ပြသည်။
- 0 သည် variable နှစ်ခုကြားတွင် linear ဆက်စပ်မှုကို ညွှန်ပြသည်။
- 1 သည် ကိန်းရှင်နှစ်ခုကြားတွင် လုံးဝအပြုသဘောဆောင်သောမျဉ်းကြောင်းဆက်စပ်မှုကို ညွှန်ပြသည်။
ဆက်စပ်ဆက်နွယ်မှုကိန်းဂဏန်းသည် သုညမှဖြစ်ပြီး၊ ကိန်းရှင်နှစ်ခုကြားရှိ ဆက်နွယ်မှုအားကောင်းလေဖြစ်သည်။
ဆက်စပ်မှု- အဘယ်အရာကို “ခိုင်မာသော” ဆက်စပ်မှုဟု ယူဆသနည်း။
သို့သော် အချို့ကိစ္စများတွင်၊ ကိန်းရှင်အတွဲများစွာကြားရှိ ဆက်စပ်မှုကို ကျွန်ုပ်တို့နားလည်လိုပါသည်။ ဤကိစ္စများတွင်၊ ကိန်းရှင်များစွာကြားရှိ ဆက်စပ်ကိန်းများကိုပြသသည့် စတုရန်းဇယားဖြစ်သည့် ဆက်စပ်မက်ထရစ်ကို ကျွန်ုပ်တို့ဖန်တီးနိုင်သည်။
Correlation Matrix ဥပမာ
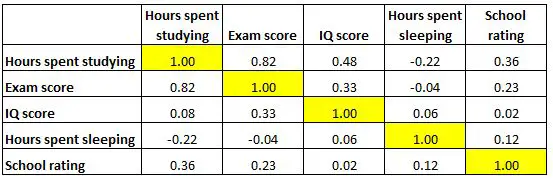
အောက်ဖော်ပြပါ ဆက်စပ်မက်ထရစ်သည် ပညာရေးဆိုင်ရာ ကိန်းရှင်များစွာကြားရှိ ဆက်စပ်ကိန်းများကို တင်ပြသည်-
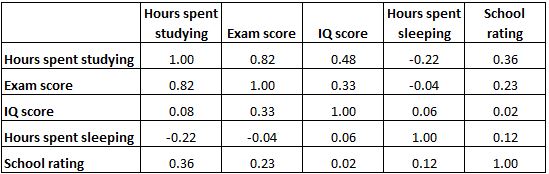
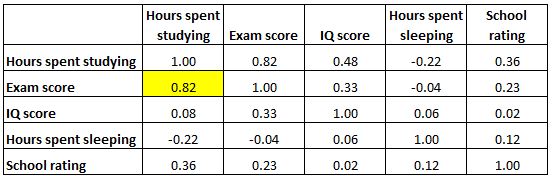
ဇယားရှိ ဆဲလ်တစ်ခုစီသည် သီးခြားကိန်းရှင်နှစ်ခုကြား ဆက်စပ်မှုကို ပြသသည်။ ဥပမာအားဖြင့်၊ အောက်ဖော်ပြပါ မီးမောင်းထိုးပြထားသောဆဲလ်သည် “ စာသင်ချိန်နာရီများ” နှင့် “ စာမေးပွဲအဆင့်” အကြားဆက်စပ်မှုသည် 0.82 ဖြစ်ပြီး ၎င်းတို့သည် အပြုသဘောဆောင်သော ဆက်နွှယ်မှုရှိကြောင်း ညွှန်ပြသည်။ စာကျက်ချိန် ပိုများနေခြင်းသည် ပိုမိုမြင့်မားသော စာမေးပွဲရမှတ်များနှင့် နီးကပ်စွာ ဆက်စပ်နေပါသည်။
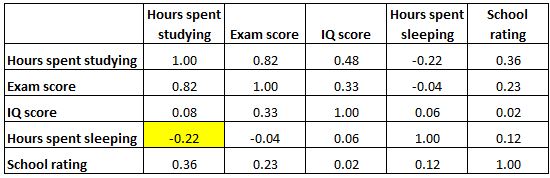
အောက်ဖော်ပြပါ မီးမောင်းထိုးပြထားသောဆဲလ်သည် “ စာကျက်ခဲ့ရတဲ့ နာရီများ” နှင့် “ အိပ်ခဲ့ရတဲ့ နာရီများ” အကြား ဆက်စပ်မှုကို -0.22 ဖြစ်ပြီး၊ ၎င်းတို့သည် အပျက်သဘောဆောင်သော ဆက်နွယ်မှုအားနည်းနေကြောင်း ညွှန်ပြသည်။ စာကျက်ချိန် ပိုများခြင်းသည် အိပ်ချိန်နည်းခြင်းနှင့် ဆက်စပ်နေသည်။
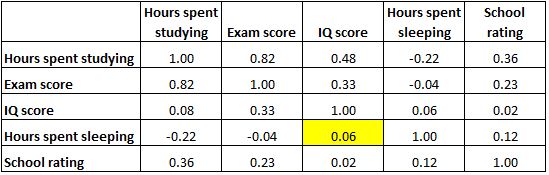
အောက်ဖော်ပြပါ မီးမောင်းထိုးပြထားသောဆဲလ်သည် “ အိပ်ခဲ့ရတဲ့နာရီများ” နှင့် “ IQ ရမှတ်” အကြား ဆက်စပ်မှုမှာ 0.06 ဖြစ်ပြီး ၎င်းတို့သည် အခြေခံအားဖြင့် ဆက်စပ်မှုမရှိကြောင်း ညွှန်ပြသည်။ ကျောင်းသားတစ်ဦး အိပ်ချိန်နှင့် ၎င်းတို့၏ IQ ရမှတ်အကြား ဆက်စပ်မှု မရှိသလောက်နည်းပါးပါသည်။
ကိန်းရှင်တစ်ခုစီသည် ၎င်းကိုယ်တိုင်နှင့် လုံးဝဆက်စပ်နေသောကြောင့် ဇယား၏ထောင့်ဖြတ်တစ်လျှောက်ရှိ ဆက်စပ်ကိန်းများကို 1 နှင့် ညီမျှကြောင်းကိုလည်း သတိပြုပါ။ ဤဆဲလ်များသည် အဓိပ္ပာယ်ဖွင့်ဆိုရန်အတွက် အသုံးမ၀င်ပါ။
ဆက်စပ်မက်ထရစ်၏ ကွဲပြားမှုများ
ဆက်စပ်မက်ထရစ်သည် ပြီးပြည့်စုံစွာ အချိုးကျကြောင်း သတိပြုပါ။ ဥပမာ၊ ညာဘက်အပေါ်ဆုံးဆဲလ်က ဘယ်ဘက်အောက်ခြေဆဲလ်နဲ့ အတိအကျတူညီတဲ့တန်ဖိုးကို ပြပါတယ်-
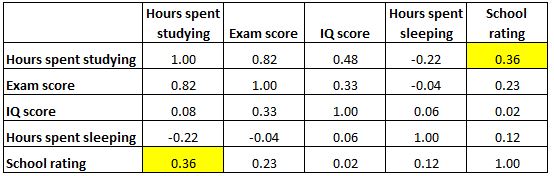
အမှန်မှာ၊ ဆဲလ်နှစ်ခုသည် “ စာကျက်ချိန်နာရီများ” နှင့် “ ကျောင်းတန်း” အကြားဆက်စပ်မှုကို တိုင်းတာသည်။
ဆက်စပ်မက်ထရစ်သည် အချိုးညီသောကြောင့်၊ မက်ထရစ်တွင်ပြသထားသော ဆက်စပ်ကိန်းများ၏ တစ်ဝက်သည် မလိုအပ်ဘဲ မလိုအပ်တော့ပါ။ ထို့ကြောင့်၊ တစ်ခါတစ်ရံတွင် ဆက်စပ်မက်ထရစ်၏ ထက်ဝက်ကိုသာ ပြသလိမ့်မည်-
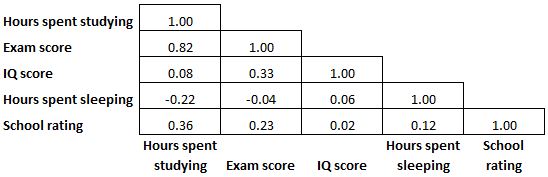
တစ်ခါတရံတွင် ဆက်စပ်ကိန်းဂဏန်းများကို ပိုမိုလွယ်ကူစွာဖတ်နိုင်ရန် အပူမြေပုံတစ်ခုကဲ့သို့ ရောင်စုံပေးပါမည်။

ဆက်စပ်မက်ထရစ်ကို ဘယ်အချိန်မှာ သုံးမလဲ။
လက်တွေ့တွင်၊ ဆက်စပ်မက်ထရစ်ကို အကြောင်းပြချက်သုံးခုအတွက် အသုံးများသည်-
1. ဆက်စပ်မက်ထရစ်သည် ဒေတာအစုတစ်စုကို အဆင်ပြေစွာ အကျဉ်းချုံးသည်။
Correlation matrix သည် data set တစ်ခုရှိ variable များအားလုံးကြားရှိ ဆက်စပ်မှုများကို အကျဉ်းချုပ်ဖော်ပြရန် ရိုးရှင်းသောနည်းလမ်းတစ်ခုဖြစ်သည်။ ဥပမာအားဖြင့်၊ ကျောင်းသား 1,000 အတွက် အောက်ပါအချက်အလက်များပါရှိသော ကျွန်ုပ်တို့တွင် အောက်ပါဒေတာအစုံရှိသည်ဆိုပါစို့။
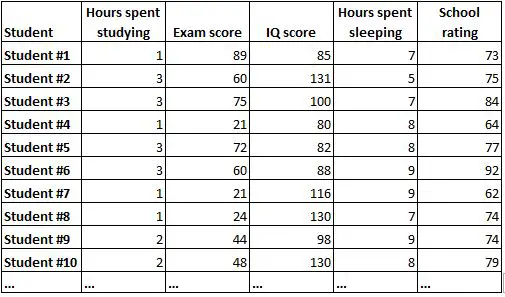
ဒေတာအကြမ်းကိုကြည့်ရုံဖြင့် ကိန်းရှင်တစ်ခုစီကြားရှိ ဆက်စပ်မှုကို နားလည်ရန် အလွန်ခက်ခဲပါသည်။ ကံကောင်းထောက်မစွာ၊ ဆက်စပ်မက်ထရစ်တစ်ခုသည် ကိန်းရှင်တစ်စုံစီကြားရှိ ဆက်နွယ်မှုများကို လျင်မြန်စွာနားလည်ရန် ကူညီပေးနိုင်ပါသည်။
2. ဆက်စပ်မက်ထရစ်သည် ဆုတ်ယုတ်ခြင်းအတွက် ရောဂါရှာဖွေမှုတစ်ခုအဖြစ် ဆောင်ရွက်သည်။
Multiple linear regression ၏ အဓိက ယူဆချက် တစ်ခုမှာ model ရှိ သီးခြား variable သည် model ရှိ အခြားသော variable များနှင့် ပြင်းပြင်းထန်ထန် ဆက်စပ်မှု မရှိခြင်း ဖြစ်သည်။
အမှီအခိုကင်းသော variable နှစ်ခုသည် အလွန်ဆက်စပ်နေသောအခါ၊ ၎င်းသည် multicollinearity ဟုခေါ်သော ပြဿနာကို ဖြစ်ပေါ်စေပြီး regression ရလဒ်များကို အနက်ဖွင့်ရန် ခက်ခဲစေသည်။
ဖြစ်နိုင်ချေရှိသော multicollinearity ပြဿနာကို ဖော်ထုတ်ရန် အရိုးရှင်းဆုံးနည်းလမ်းတစ်ခုမှာ ဆက်စပ်မက်ထရစ်ကိုကြည့်ရန်နှင့် ကိန်းရှင်များတစ်ခုနှင့်တစ်ခု အလွန်ဆက်စပ်မှုရှိမရှိကို အမြင်အာရုံဖြင့် စစ်ဆေးခြင်းဖြစ်သည်။
3. ဆက်စပ်မက်ထရစ်ကို အခြားခွဲခြမ်းစိတ်ဖြာမှုများအတွက် ထည့်သွင်းမှုအဖြစ် အသုံးပြုနိုင်သည်။
ဆက်စပ်မက်ထရစ်ကို စူးစမ်းလေ့လာရေးအချက်ခွဲခြမ်းစိတ်ဖြာခြင်းနှင့် ဖွဲ့စည်းတည်ဆောက်ပုံဆိုင်ရာ ညီမျှခြင်းပုံစံများကဲ့သို့သော အခြားရှုပ်ထွေးသောခွဲခြမ်းစိတ်ဖြာမှုများအတွက် ထည့်သွင်းမှုအဖြစ် အသုံးပြုသည်။
ထပ်လောင်းအရင်းအမြစ်များ
အောက်ဖော်ပြပါ သင်ခန်းစာများသည် ကိန်းဂဏန်းဆိုင်ရာဆော့ဖ်ဝဲလ်ကို အသုံးပြု၍ ဆက်စပ်မက်ထရစ်တစ်ခုကို မည်သို့ဖန်တီးရမည်ကို ရှင်းပြသည်-
Excel တွင် Correlation Matrix ဖန်တီးနည်း
SPSS တွင် Correlation Matrix ကိုဖန်တီးနည်း
Stata တွင် ဆက်စပ်မက်ထရစ်တစ်ခုကို ဖန်တီးနည်း
Python တွင် Correlation Matrix ကိုဖန်တီးနည်း