ကိန်းရှင်များကြား ဆက်စပ်မှုမရှိခြင်း ဥပမာ ၄
ကိန်းဂဏန်းစာရင်းဇယားများတွင် ဆက်စပ်မှု ဆိုသည်မှာ ကိန်းရှင်နှစ်ခုကြားရှိ မျဉ်းကြောင်းဆက်နွယ်မှုကို တိုင်းတာခြင်းဖြစ်သည်။
ဆက်စပ်ကိန်း၏တန်ဖိုးသည် -1 နှင့် 1 ကြားတွင် အမြဲရှိနေသည်-
- -1 သည် ကိန်းရှင်နှစ်ခုကြားတွင် လုံးဝအပျက်သဘောဆောင်သော ဆက်စပ်ဆက်နွယ်မှုကို ညွှန်ပြသည်။
- 0 သည် variable နှစ်ခုကြားတွင် linear ဆက်စပ်မှုမရှိဟု ညွှန်ပြသည်။
- 1 သည် ကိန်းရှင်နှစ်ခုကြားတွင် လုံးဝအပြုသဘောဆောင်သောမျဉ်းကြောင်းဆက်စပ်မှုကို ညွှန်ပြသည်။
ကိန်းရှင်နှစ်ခုသည် သုည၏ဆက်စပ်မှုရှိပါက၊ ၎င်းတို့သည် မည်သည့်နည်းနှင့်မျှ မဆက်စပ်ကြောင်း ညွှန်ပြသည်။ တစ်နည်းဆိုရသော်၊ ကိန်းရှင်တစ်ခု၏တန်ဖိုးကို သိရှိခြင်းသည် အခြားကိန်းရှင်၏တန်ဖိုးသည် မည်သို့ဖြစ်နိုင်သည်ကို ကျွန်ုပ်တို့မသိနိုင်ပေ။
အကယ်၍ ကျွန်ုပ်တို့သည် သုညဆက်စပ်မှုရှိသော ကိန်းရှင်နှစ်ခု၏ အပိုင်းအစတစ်ခုကို ဖန်တီးပါက၊ ဂရပ်တွင် ရှင်းလင်းပြတ်သားသောပုံစံရှိမည်မဟုတ်ပါ။
No Correlation နမူနာများ
အောက်ဖော်ပြပါ ဥပမာများသည် ကိန်းရှင်နှစ်ခုတွင် ဆက်စပ်မှုမရှိသော အဖြစ်အပျက်များကို သရုပ်ဖော်သည်။
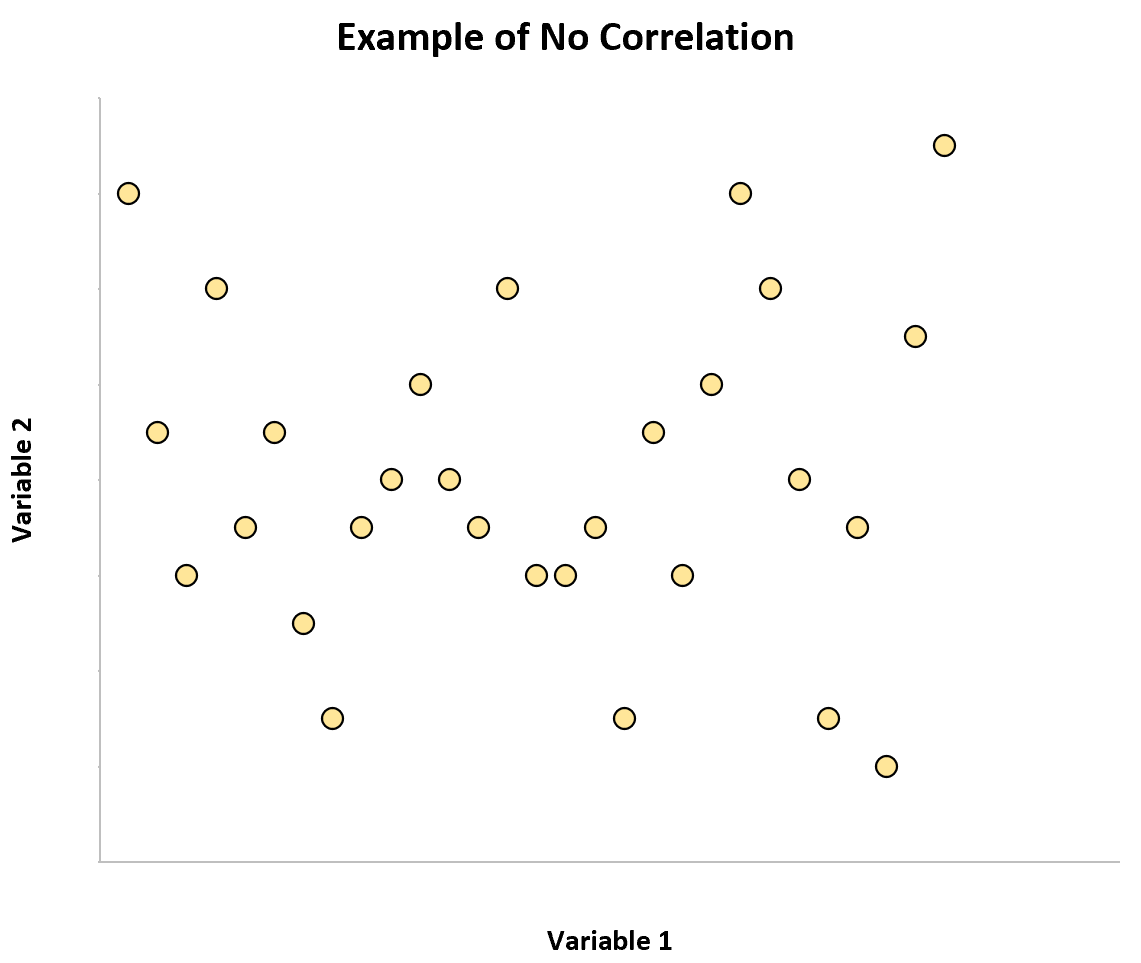
ဥပမာ 1- ကော်ဖီစားသုံးမှုနှင့် ထောက်လှမ်းရေး
လူတစ်ဦးချင်းစီသောက်သုံးသော ကော်ဖီပမာဏနှင့် ၎င်းတို့၏ IQ အဆင့်သည် လုံးဝဆက်စပ်မှုမရှိပါ။ တစ်နည်းဆိုရသော် လူတစ်ယောက်သည် ကော်ဖီမည်မျှသောက်သည်ကို သိခြင်းသည် ၎င်းတို့၏ IQ အဆင့်ကို အကြံဥာဏ်မပေးပေ။
အကယ်၍ ကျွန်ုပ်တို့သည် နေ့စဉ် ကော်ဖီသောက်သုံးမှု၏ IQ အဆင့်နှင့် နှိုင်းယှဉ်ပါက၊ ၎င်းသည် ဤကဲ့သို့ ဖြစ်သည်-
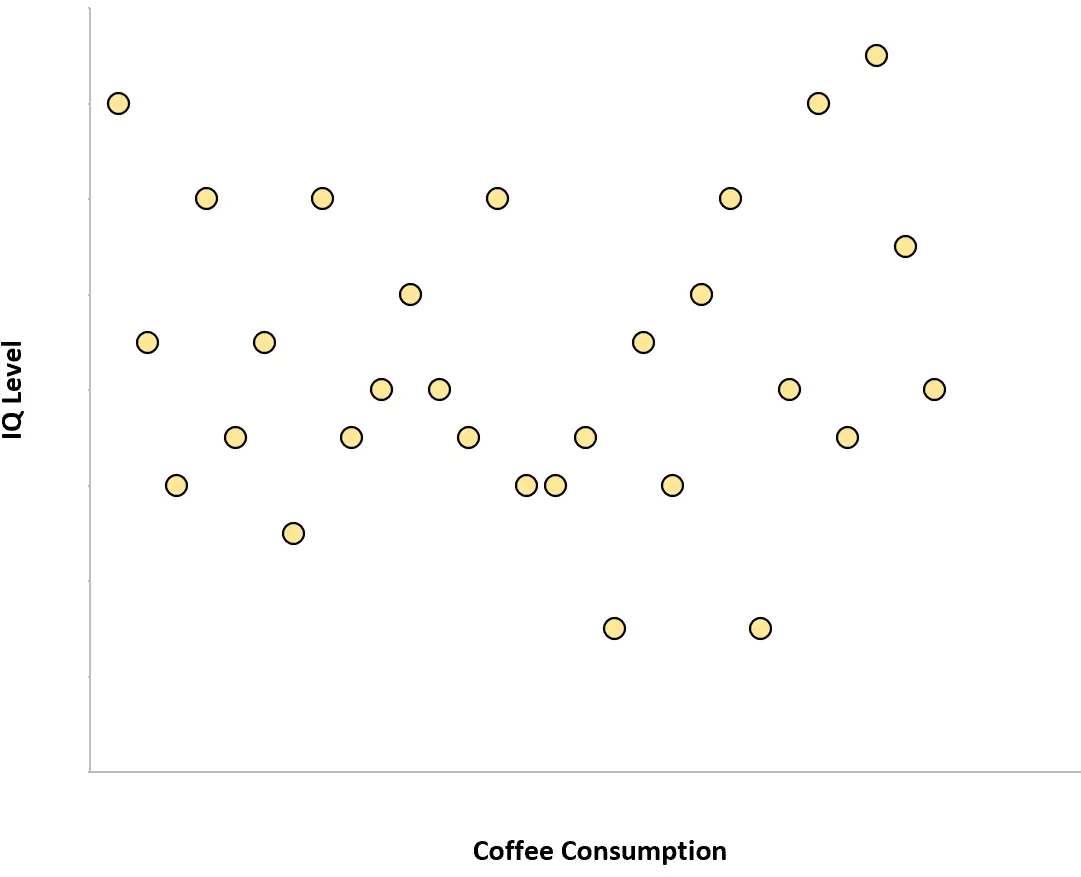
ဥပမာ 2- အမြင့်နှင့် စာမေးပွဲရမှတ်များ
ကျောင်းသားများ၏ အမြင့်နှင့် ၎င်းတို့၏ ပျမ်းမျှ စာမေးပွဲရမှတ်များသည် သုည၏ ဆက်စပ်မှုရှိသည်။ တစ်နည်းဆိုရသော် လူတစ်ဦးချင်းစီ၏ အရပ်အမြင့်ကို သိရှိခြင်းသည် ၎င်းတို့၏ ပျမ်းမျှ စာမေးပွဲရမှတ်ကို အကြံဥာဏ်မပေးပေ။
အကယ်၍ ကျွန်ုပ်တို့သည် အရပ်အမြင့်နှင့် ပျမ်းမျှ စာမေးပွဲရမှတ်ကို ကိုယ်စားပြုသည့် အပိုင်းအစတစ်ခုကို ဖန်တီးပါက၊ ၎င်းသည် ဤကဲ့သို့ ဖြစ်လိမ့်မည်-
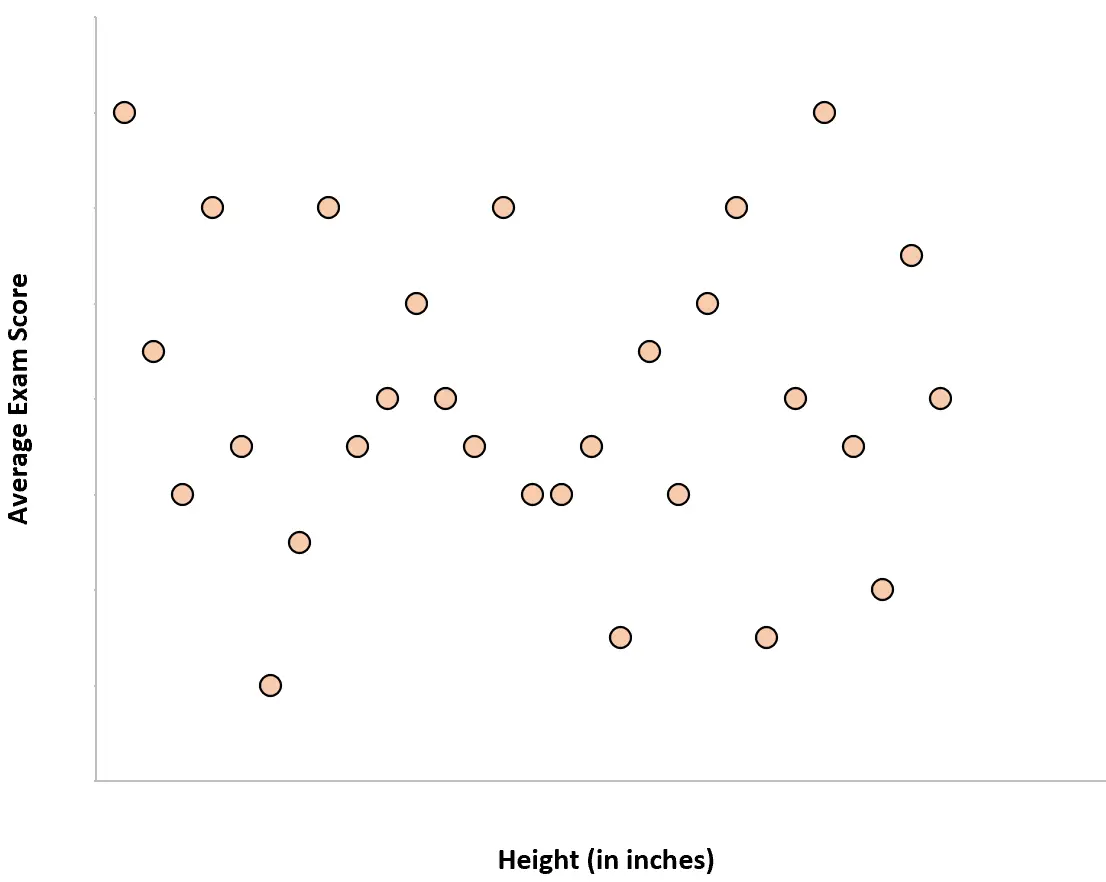
ဥပမာ 3- ဖိနပ်အရွယ်အစားနှင့် ရုပ်ရှင်များကို ကြည့်သည်။
လူတစ်ဦးချင်းစီ၏ ဖိနပ်အရွယ်အစားနှင့် တစ်နှစ်လျှင် ၎င်းတို့ကြည့်ရှုသည့် ရုပ်ရှင်အရေအတွက်သည် လုံးဝဆက်စပ်မှုမရှိပါ။ တစ်နည်းဆိုရသော် လူတစ်ဦးချင်းစီ၏ ဖိနပ်အရွယ်အစားကို သိရှိခြင်းသည် တစ်နှစ်လျှင် ရုပ်ရှင်မည်မျှကြည့်ရှုမည်ကို စိတ်ကူးမယဉ်နိုင်ပေ။
ကြည့်ဖူးသည့် ရုပ်ရှင်အရေအတွက်နှင့် ဖိနပ်အရွယ်အစား ကွဲပြားသော ကွက်ကွက်တစ်ခုကို ဖန်တီးပါက၊ ၎င်းသည် ဤကဲ့သို့ ဖြစ်နေမည်-
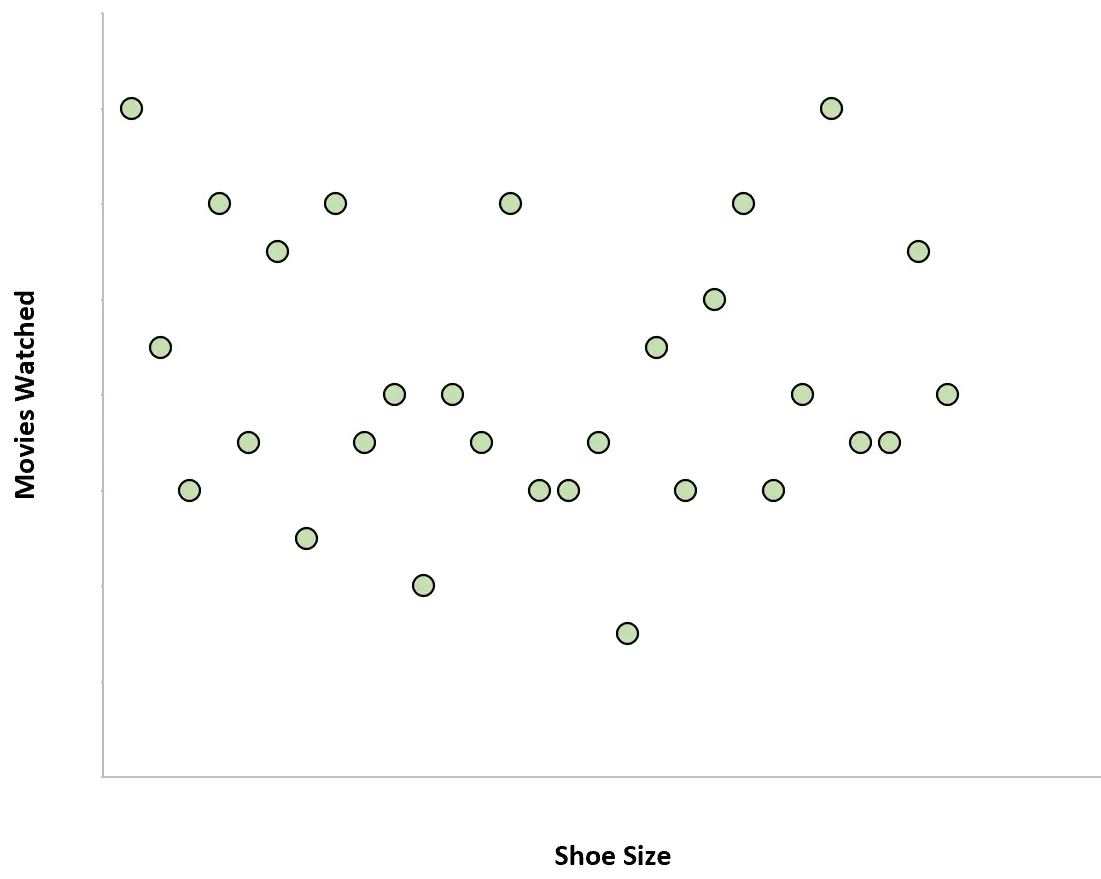
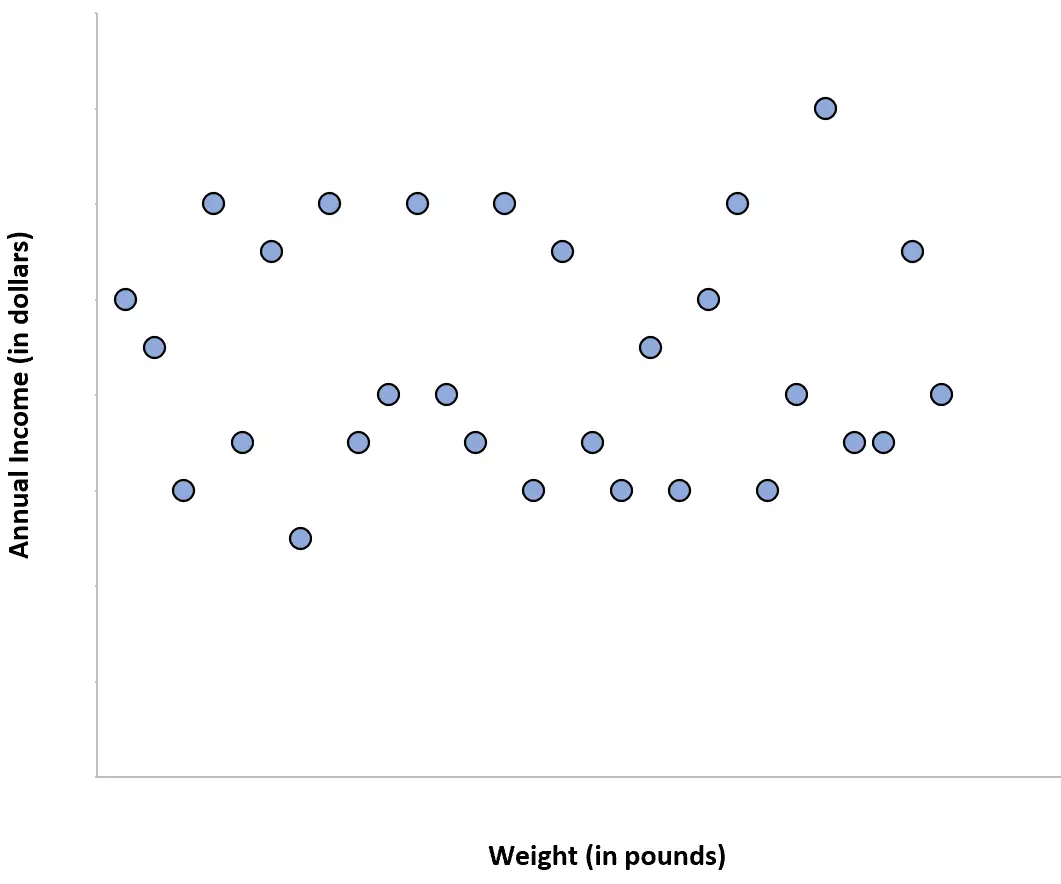
ဥပမာ 4- ကိုယ်အလေးချိန်နှင့် ဝင်ငွေ
လူတစ်ဦးချင်းစီ၏ အလေးချိန်နှင့် ၎င်းတို့၏ နှစ်စဉ်ဝင်ငွေသည် လုံးဝဆက်စပ်မှုမရှိပါ။ တစ်နည်းဆိုရသော် လူတစ်ဦး၏ ကိုယ်အလေးချိန်ကို သိရှိခြင်းသည် ၎င်းတို့၏ တစ်နှစ်တာ ၀င်ငွေ မည်မျှရှိသည်ကို အကြံဉာဏ်ပေးမည်မဟုတ်ပေ။
အကယ်၍ ကျွန်ုပ်တို့သည် အလေးချိန်/ဝင်ငွေ ခွဲခြမ်းစိတ်ဖြာမှု အစီအစဉ်တစ်ခုကို ဖန်တီးပါက၊ ၎င်းသည် ဤကဲ့သို့ ဖြစ်လိမ့်မည်-
ထပ်လောင်းအရင်းအမြစ်များ
Pearson Correlation Coefficient နိဒါန်း
ဆက်စပ်မှု vs. အသင်းအဖွဲ့- ကွာခြားချက်ကဘာလဲ။
ဆက်စပ်မှုနှင့် ဆုတ်ယုတ်မှု- ကွာခြားချက်ကား အဘယ်နည်း။