ဆုံးဖြတ်ချက်သစ်ပင်

ဤဆောင်းပါးတွင် ဆုံးဖြတ်ချက်သစ်ပင်များကို မည်သည့်အရာနှင့် ၎င်းတို့အတွက် အသုံးပြုကြောင်း ရှင်းပြထားသည်။ ထို့အပြင်၊ ၎င်းသည် ဆုံးဖြတ်ချက်သစ်တစ်ခုဖန်တီးပုံနှင့် အဆင့်ဆင့်ဖြေရှင်းထားသော လေ့ကျင့်ခန်းတစ်ခုကိုလည်း ပြသထားသည်။ နောက်ဆုံးတွင်၊ ဆုံးဖြတ်ချက်သစ်ပင်ကိုအသုံးပြုခြင်း၏ အားသာချက်များနှင့် အားနည်းချက်များကို သင်တွေ့မြင်နိုင်မည်ဖြစ်သည်။

ဆုံးဖြတ်ချက်သစ်ပင်ဆိုတာ ဘာလဲ။

ဆုံးဖြတ်ချက်သစ်ပင် သည် ပြုလုပ်ရမည့် ဆုံးဖြတ်ချက်များ၊ ဖြစ်ပေါ်လာနိုင်သည့် မတူညီသော အခြေအနေများနှင့် ဖြစ်နိုင်သည့်ရလဒ်အားလုံးကို ကိုယ်စားပြုသည့် ပုံကြမ်းတစ်ခုဖြစ်သည်။ ထို့ကြောင့် ဆုံးဖြတ်ချက်သစ်ပင်သည် ဖြစ်နိုင်ချေရှိသော အခြေအနေများစွာကို ထည့်သွင်းစဉ်းစားရမည့် ဆုံးဖြတ်ချက်အကူအညီတစ်ခုအဖြစ် ဆောင်ရွက်ပေးပါသည်။

ဆုံးဖြတ်ချက်သစ်ပင်သည် ဆုံးဖြတ်ချက်များချရာတွင် အလွန်အသုံးဝင်သော ကိရိယာတစ်ခုဖြစ်ပြီး အခြားရွေးချယ်စရာတစ်ခုစီ၏ ဖြစ်နိုင်ခြေရှိသော အကျိုးဆက်များနှင့် ဆုံးဖြတ်ချက်တစ်ခုစီတိုင်းတွင် မည်သည့်ရလဒ်များ အောင်မြင်နိုင်သည်ကို မြင်ယောင်နိုင်စေသောကြောင့် ဖြစ်သည်။

ထို့ကြောင့် ဆုံးဖြတ်ချက်သစ်ပင်သည် စီးပွားရေးဆိုင်ရာ ဆုံးဖြတ်ချက်များကို ခွဲခြမ်းစိတ်ဖြာရာတွင် တွင်ကျယ်စွာအသုံးပြုသည့် ပုံကြမ်းအမျိုးအစားတစ်ခုဖြစ်ပြီး၊ ဖြစ်နိုင်သောစီးပွားရေးကုန်ကျစရိတ်များ သို့မဟုတ် မျှော်မှန်းထားသောအကျိုးအမြတ်များကို ဂရပ်ဖစ်ဖြင့်ဖော်ပြနိုင်စေသောကြောင့်ဖြစ်သည်။

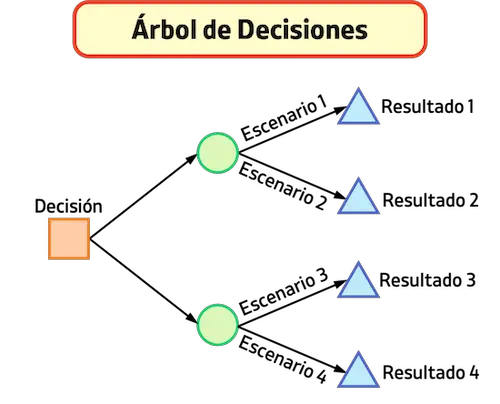
ပုံမှန်အားဖြင့်၊ ဆုံးဖြတ်ချက်တစ်ခုချသည့်အခါတိုင်း၊ အခြေအနေများစွာ ဖြစ်နိုင်သည်။ ထို့ကြောင့်၊ ဆုံးဖြတ်ချက်သစ်ပင်သည် ဖြစ်နိုင်ခြေရှိသော အခြေအနေများအားလုံးကို တစ်ကမ္ဘာလုံးအတိုင်းအတာဖြင့် မြင်နိုင်ရန် ကူညီပေးသည်၊ ၎င်းသည် ဆုံးဖြတ်ချက်တစ်ခုစီတိုင်းသည် မည်မျှအန္တရာယ်များကြောင်း သိနိုင်စေပါသည်။

ဆုံးဖြတ်ချက်သစ်ပင်တစ်ခုသည် သစ်ပင်ပုံသဏ္ဍာန်နှင့် ကွဲပြားသည်ကို သတိပြုပါ၊ ၎င်းတို့တွင် အလားတူအမည်များရှိပြီး အမှန်တကယ်တွင် လက္ခဏာများစွာကို မျှဝေထားသည်။ ဆုံးဖြတ်ချက်သစ်ပင်ဆိုသည်မှာ ဆုံးဖြတ်ချက်သစ်ပင်နှင့် မည်သို့ကွာခြားသည်ကို သိရှိရန် ဤနေရာကို နှိပ်ပါ။

ဆုံးဖြတ်ချက်သစ်ပင်၏ အစိတ်အပိုင်းများ

ဆုံးဖြတ်ချက်သစ်ပင်ကို အောက်ပါအချက်များဖြင့် ဖွဲ့စည်းထားပါသည်။

• ဆုံးဖြတ်ချက်အမှတ် (□) : ဆုံးဖြတ်ချက်တစ်ခုနှင့် ကိုက်ညီသည်။ ဆုံးဖြတ်ချက်သစ်တွင် ၎င်းကို စတုရန်းတစ်ခုဖြင့် ကိုယ်စားပြုသည်။
• Probability node (○) – များပြားလှသော မြင်ကွင်းများ ဖြစ်ပေါ်လာနိုင်သည်ကို ကိုယ်စားပြုသည်၊ ဖြစ်နိုင်ခြေ node တစ်ခုစီမှ ထွက်လာသော အကိုင်းအခက်တစ်ခုစီသည် မတူညီသော မြင်ကွင်းတစ်ခုကို ကိုယ်စားပြုသည်။ ၎င်းကို ဆုံးဖြတ်ချက်သစ်ပင်ရှိ စက်ဝိုင်းအလွတ်ဖြင့် ရေးဆွဲထားသည်။
• Final node (△) : ရလဒ်ကို ကိုယ်စားပြုသည်၊ ထို့ကြောင့် အကိုင်းအခက်မရှိသောကြောင့် ၎င်းတို့ကို အလွယ်တကူ ခွဲခြားသတ်မှတ်နိုင်သည်။ ဆုံးဖြတ်ချက်သစ်တွင် ၎င်းတို့ကို တြိဂံများဖြင့် ကိုယ်စားပြုသည်။

ဆုံးဖြတ်ချက်ချနည်းသစ်ပင်

ဆုံးဖြတ်ချက်သစ်တစ်ခုဖန်တီးရန်၊ အောက်ပါအဆင့်များကို လိုက်နာရပါမည်-

1. အဓိက ဆုံးဖြတ်ချက်ကို ကိုယ်စားပြုခြင်း – ဆုံးဖြတ်ချက်သစ်ကို ဖန်တီးရာတွင် ပထမအဆင့်မှာ ပုံကြမ်းပေါ်တွင် ပြုလုပ်ရမည့် ပထမဆုံး ဆုံးဖြတ်ချက်ကို ကိုယ်စားပြုရန် ဖြစ်သည်။ ဒီလိုလုပ်ဖို့၊ ဆုံးဖြတ်နိုင်တဲ့ ဖြစ်နိုင်တဲ့ရွေးချယ်မှုတစ်ခုစီအတွက် စတုရန်းတစ်ခုနဲ့ မြှားတစ်စင်းကို ဆွဲလိုက်ပါ။
2. ဆုံမှတ်များထည့်ပါ – ယခင်အဆင့်တွင်ရေးဆွဲထားသော အကိုင်းအခက်တစ်ခုစီတွင်၊ ဆုံးဖြတ်ချက်နှင့် ဖြစ်နိုင်ခြေ ဆုံမှတ်များပေါင်းထည့်ခြင်းဖြင့် ဆုံးဖြတ်ချက်သစ်ကို ချဲ့ထွင်ပါ။
3. ဝင်ရောက်ခွင့် ရလဒ် – ဆုံးဖြတ်ချက် နှင့် ဖြစ်နိုင်ခြေ ဆုံမှတ်များကို ဆက်လက်ပေါင်းထည့်ခြင်း ၊ အကိုင်းအခက် တစ်ခုစီ မှ နောက်ဆုံး node သို့မဟုတ် ရလဒ်များ မရောက်ရှိမချင်း ဆက်လက်လုပ်ဆောင်ပါ။ လမ်းကြောင်းအားလုံးသည် ရလဒ်တစ်ခုဆီသို့ ဦးတည်သွားသောအခါတွင် သင်သည် ဆုံးဖြတ်ချက်သစ်ပင်ကို ပြီးမြောက်စေမည်ဖြစ်သည်။
4. ဆုံးဖြတ်ချက်တစ်ခုချပါ – ဆုံးဖြတ်ချက်သစ်ကို ပြီးသွားသည်နှင့်၊ ၎င်းကို ခွဲခြမ်းစိတ်ဖြာပြီး ဘာလုပ်သင့်သည်များကို ဆုံးဖြတ်ပါ။

ဆုံးဖြတ်ချက်သစ်ပင်သည် ဆုံးဖြတ်ချက်တစ်ခုကို ပေးစွမ်းမည်မဟုတ်ကြောင်း သတိပြုပါ၊ ၎င်းသည် ဆုံးဖြတ်ရာတွင် အထောက်အကူဖြစ်သည်။ နောက်ဆုံး ဆုံးဖြတ်ချက်ကို သင်က ဆုံးဖြတ်ရမှာ ဖြစ်ပါတယ်။ အောက်တွင် မတူညီသော ဖြစ်နိုင်ခြေရှိသော အခြေအနေများကို ခွဲခြမ်းစိတ်ဖြာပြီး အကောင်းဆုံး ဆုံးဖြတ်ချက်ချရန် ဆုံးဖြတ်ချက်သစ်ပင်ကို မည်သို့အသုံးပြုရမည်ကို အောက်တွင် တွေ့ရမည်ဖြစ်ပါသည်။

ဆုံးဖြတ်ချက်သစ်ပင် ဥပမာ

ဆုံးဖြတ်ချက်သစ်ပင်၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ၎င်းကို အောင်မြင်ပုံပေါ်သည့် သီအိုရီကို ကြည့်ရှုပြီးနောက်၊ သဘောတရားကို အပြည့်အဝနားလည်ရန် ခိုင်မာသော ဥပမာတစ်ခုကို ကျွန်ုပ်တို့ မြင်တွေ့ရမည်ဖြစ်သည်။

ကုမ္ပဏီတစ်ခုသည် ၎င်း၏စွမ်းဆောင်ရည်ကို လာမည့် ၅ နှစ်အထိ တိုးချဲ့ရန် စီစဉ်နေသည်။ လက်ရှိ တိုးတက်မှုသည် ကောင်းမွန်သော်လည်း နောက်ဆုံးတွင် စီးပွားရေး ဆုတ်ယုတ်လာပါက သိသိသာသာ တိုးလာမည်ဟု ခန့်မှန်းထားသည် (ဤဖြစ်နိုင်ခြေမှာ ခန့်မှန်းခြေ 40%) ဖြစ်သည်။

ရွေးချယ်စရာများသည် ယခင်အတိုင်း ဆက်လုပ်ရန်၊ ပိုကြီးသော တည်နေရာသို့ ရွှေ့ရန် သို့မဟုတ် ၎င်းတို့တွင် လက်ရှိရှိနေသည့်နေရာကို ချဲ့ထွင်ရန်ဖြစ်သည်။ ပထမနှစ်တွင် ဘာဖြစ်မည်ကို စောင့်ဆိုင်းပြီး တိုးတက်မှုရှိလာပါက တိုးချဲ့လုပ်ဆောင်ရန်လည်း အလားအလာရှိမည်ဖြစ်သည်။ ကိစ္စရပ်တိုင်းတွင် ရရှိမည့် စီးပွားရေးအားသာချက်မှာ အောက်ပါအတိုင်းဖြစ်သည်။

• လွှဲပြောင်းမှု-
  • ခိုင်မာသောတိုးတက်မှု- $800,000
  • အနိမ့်ဆုံးတိုးတက်မှု- $100,000
• တိုးချဲ့မှု-
  • ခိုင်မာသောတိုးတက်မှု- $800,000
  • အနိမ့်ဆုံးတိုးတက်မှု- $100,000
• ဘာမှ မလုပ်ပါနဲ့
  • ခိုင်မာသောတိုးတက်မှု + တိုးချဲ့မှု ဒုတိယနှစ်- $500,000
  • ခိုင်မာသောတိုးတက်မှု + ဘာမှမလုပ်ပါ- $450,000
  • အနိမ့်ဆုံးတိုးတက်မှု- $400,000

ပြဿနာထုတ်ပြန်ချက်က ကျွန်ုပ်တို့ကိုပေးထားသည့် အချက်အလက်အားလုံးအပေါ် အခြေခံ၍ ကျွန်ုပ်တို့သည် ပြုလုပ်ရမည့် ဆုံးဖြတ်ချက်များ၊ ထည့်သွင်းစဉ်းစားထားသော အခြေအနေများစွာနှင့် ဆုံးဖြတ်ချက်သစ်ပင်ရှိ ဖြစ်နိုင်သမျှရလဒ်အားလုံးကို ကိုယ်စားပြုနိုင်ပါသည်။

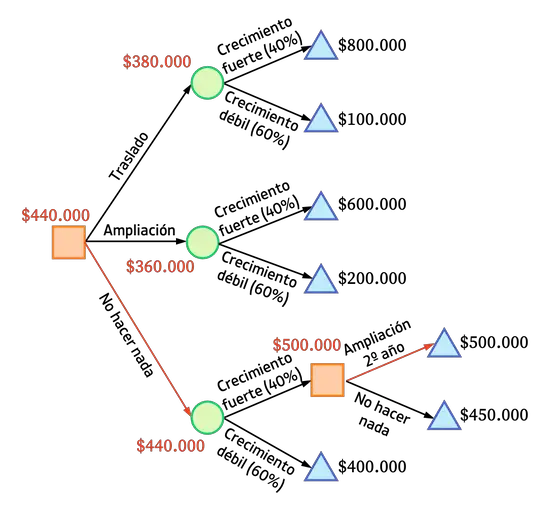
ထို့ကြောင့် ဤကိစ္စအတွက် ဆုံးဖြတ်ချက်သစ်မှာ အောက်ပါအတိုင်းဖြစ်သည်။

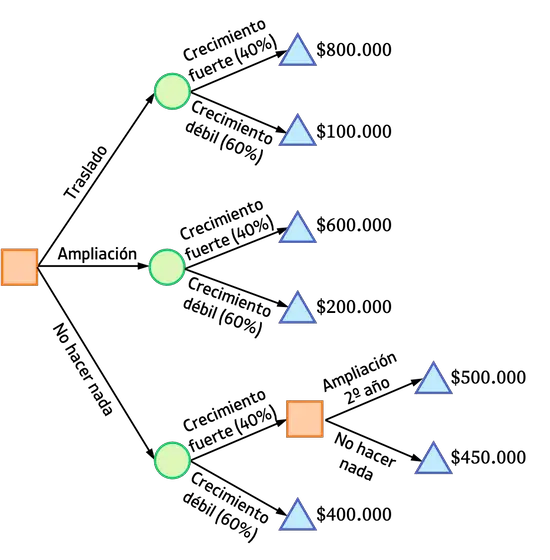
ယခု ကျွန်ုပ်တို့သည် ဆုံးဖြတ်ချက်သစ်ပင်ကို ထူထောင်ထားသောကြောင့် ၎င်းကို ခွဲခြမ်းစိတ်ဖြာပြီး အပြီးသတ်ဆုံးဖြတ်ချက်ချရန် အချိန်တန်ပြီဖြစ်သည်။ နောက်အပိုင်းတွင်၊ သင့်ဆုံးဖြတ်ချက်ကို ဆုံးဖြတ်ရန် သင်အသုံးပြုနိုင်သည့် ကွဲပြားခြားနားသောစံနှုန်းများကို သင့်အား ပြသထားသည်။

ဆုံးဖြတ်ချက်သစ်ပင်တွင် ဆုံးဖြတ်ချက်စံနှုန်းများ

ဆုံးဖြတ်ချက်သစ်ကိုအသုံးပြု၍ မည်သည့်ဆုံးဖြတ်ချက်ကိုချရမည်ကို ဆုံးဖြတ်ရန် အဓိကအားဖြင့် စံသုံးရပ်ရှိသည်- အဆိုးမြင်မှုစံနှုန်း၊ အကောင်းမြင်မှုစံနှုန်းနှင့် သင်္ချာဆိုင်ရာ မျှော်မှန်းချက်စံနှုန်းတို့ဖြစ်သည်။ အောက်မှာ သူတို့တစ်တွေစီမှာ ဘာတွေပါဝင်လဲဆိုတာကို ကြည့်လိုက်ကြရအောင်။

အဆိုးမြင်မှုစံနှုန်း

အဆိုးမြင်မှု သို့မဟုတ် ရှေးရိုးဆန်သော စံနှုန်းများက ဖြစ်နိုင်ခြေ အဆိုးဆုံး အခြေအနေ ဖြစ်ပေါ်လာမည်ဟု ဆိုသည်။ ထို့ကြောင့်၊ ဤစံသတ်မှတ်ချက်တွင်၊ ဖြစ်ရပ်မှန်သည် ယူဆသူအားလုံး၏ အဆိုးဆုံးဖြစ်သောအခါတွင် အကောင်းဆုံးရလဒ်ကိုပေးမည့် ရွေးချယ်မှုကို ရွေးချယ်သည်။

အဆိုးမြင်စံနှုန်းကို အသုံးပြု၍ အထက်ဖော်ပြပါ ဥပမာကို လိုက်နာပါက၊ ကုမ္ပဏီ၏တိုးတက်မှုနှုန်းနည်းပါက ကျွန်ုပ်တို့သည် ပိုမိုအမြတ်အစွန်း (ဒေါ်လာ 400,000) ရရှိမည်ဖြစ်သောကြောင့်၊ ကျွန်ုပ်တို့သည် ယခင်အတိုင်း ဆက်လက်လုပ်ဆောင်ရန် ဆုံးဖြတ်ပြီး မည်သည့်အရာကိုမျှ မလုပ်လိုပါ။

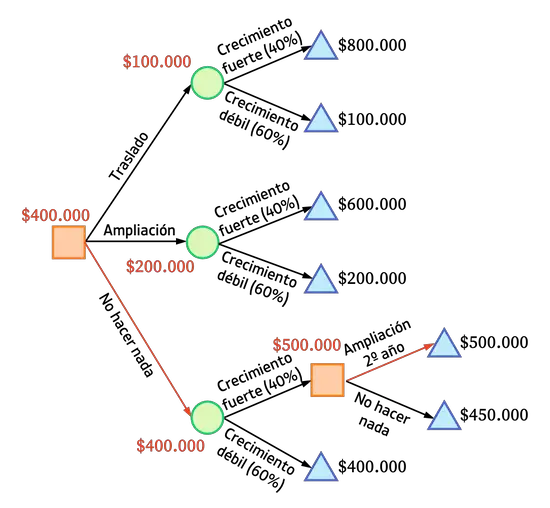
အဆိုးမြင်မှုစံနှုန်းကို အသုံးပြုခြင်းဖြင့်၊ ဤအခြေအနေတွင် ဒေါ်လာ 400,000 ဖြစ်သည့် အနည်းဆုံးရလဒ်ကို ကျွန်ုပ်တို့အာမခံပါသည်။ ဒါကြောင့် နောက်ဆုံးမှာ ကျွန်တော်တို့ ကံကောင်းပြီး ပိုကောင်းတဲ့ အဖြစ်အပျက်တစ်ခု ဖြစ်လာရင်၊ ပိုကောင်းတဲ့ ရလဒ်ကို ရရှိမှာပါ။ ဒါပေမယ့် ဘယ်လိုအခြေအနေမျိုးမှာမှ ကျွန်တော်တို့ ပိုဆိုးတဲ့ ရလဒ်တွေကို ရရှိနိုင်မှာ မဟုတ်ပါဘူး။

ကျွန်ုပ်တို့သည် ဤစံနှုန်းကိုအသုံးပြုသည့်အခါ အနာဂတ်အခြေအနေသည် အနုတ်လက္ခဏာဖြစ်မည်ဟု ကျွန်ုပ်တို့ထင်လျှင်ပင်၊ ကျွန်ုပ်တို့သည် ဤအဆိုးမြင်မှုအခြေအနေတွင် ပိုမိုကောင်းမွန်သောရလဒ်ရရှိမည့်ရွေးချယ်မှုကို ယုတ္တိရှိရှိရွေးချယ်ရမည်ဖြစ်သည်။ အဆိုးဆုံးရလဒ်ကိုပေးမည့် option ကိုရွေးချယ်ခြင်းသည် မှားယွင်းနေပေလိမ့်မည်။ ကျွန်ုပ်တို့သည် ကျွန်ုပ်တို့၏ ထိန်းချုပ်မှုအတွင်း အရာအားလုံးကို အမြင့်ဆုံးဖြစ်အောင် လုပ်ဆောင်ရမည်ဖြစ်သည်။

အကောင်းမြင်မှုစံနှုန်း

အကောင်းမြင်မှုစံနှုန်းက ဖြစ်ပေါ်လာမည့် အခြေအနေသည် အကောင်းဆုံးဖြစ်နိုင်သည်ဟု ဖော်ပြထားသည်။ ထို့ကြောင့်၊ ဤစံနှုန်းကိုအသုံးပြုသောအခါ၊ အခြေအနေသည် အခွင့်သာသောအခါတွင် ပိုမိုကောင်းမွန်သောရလဒ်ကို ရရှိစေမည့် ရွေးချယ်မှုကို ကျွန်ုပ်တို့ရွေးချယ်သည်။

ယခင်နမူနာကို လိုက်နာပါက၊ အထူးသဖြင့် ကုမ္ပဏီ၏အမြတ်ငွေ $800,000 ဖြစ်ပါက ကုမ္ပဏီ၏တိုးတက်မှုအားကောင်းပါက ပိုမိုကောင်းမွန်သောရလဒ်ကို ရရှိမည်ဖြစ်သောကြောင့် ကုမ္ပဏီကိုပြောင်းရွှေ့ရန် ဆုံးဖြတ်မည်ဖြစ်သည်။

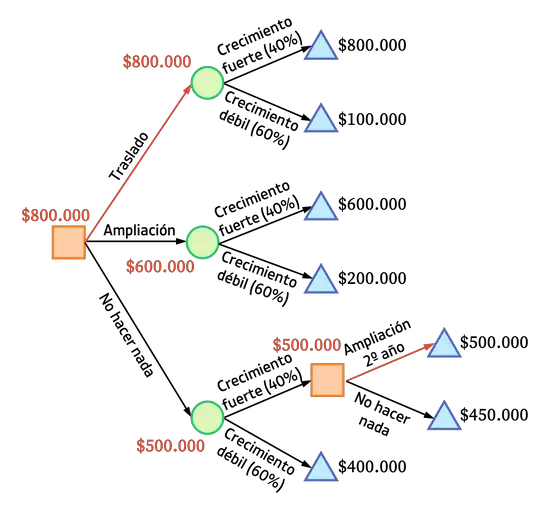
အကောင်းမြင်သောစံနှုန်းကို ဆုံးဖြတ်ရန်အသုံးပြုသောအခါ ရလဒ်သည် အလွန်ကောင်းမွန်နိုင်သော်လည်း၊ ဇာတ်လမ်းက အဆင်မပြေဘဲ အဆုံးသတ်ပါက အလွန်ညံ့ဖျင်းသောရလဒ်ကို ရရှိတတ်သည်။

သင်္ချာမျှော်လင့်ချက်စာမေးပွဲ

ဤစံသတ်မှတ်ချက်တွင် အခြားရွေးချယ်စရာများအားလုံး၏ သင်္ချာမျှော်လင့်ချက်ကို တွက်ချက်ခြင်း ပါဝင်သည်၊ ထို့ကြောင့် ပိုမိုမြင့်မားသောရလဒ်ကိုရရှိသောရွေးချယ်မှုသည် ရွေးချယ်ထားသည့်အရာဖြစ်သည်။

ဆောင်းပါးကဲ့သို့ပင်၊ ကျွန်ုပ်တို့ရွေးချယ်သင့်သည့် ရွေးချယ်မှုသည် မည်သည့်အရာမှ မလုပ်ဘဲ ကုမ္ပဏီကို ထားခဲ့ရန်ဖြစ်ပြီး ၎င်းသည် မျှော်မှန်းတန်ဖိုး အမြင့်ဆုံးသော ရွေးချယ်မှုဖြစ်သောကြောင့် ၎င်းသည် ၎င်းသည် ကုမ္ပဏီကို ထားခဲ့ပါ။ အမြင့် (၄၄၀၀၀၀)ကျပ်။

ဆုံးဖြတ်ချက်ချခြင်းလုပ်ငန်းစဉ်ကို အကြိမ်ပေါင်းများစွာ ထပ်ခါတလဲလဲလုပ်ရသည့်အခါ ဤစံသတ်မှတ်ချက်သည် အလွန်အသုံးဝင်သည်၊ အကြောင်းမှာ သင်္ချာဆိုင်ရာမျှော်လင့်ချက်သည် ပျမ်းမျှအကောင်းဆုံးဆုံးဖြတ်ချက်များကို ပေးဆောင်သောကြောင့်ဖြစ်သည်။ သို့သော် ဆုံးဖြတ်ချက်ကို တစ်ကြိမ်သာ ပြုလုပ်ပါက၊ ယင်းသည် အသင့်လျော်ဆုံး စံသတ်မှတ်ချက် မဟုတ်ပေ။

ဆုံးဖြတ်ချက် မက်ထရစ် ကဲ့သို့သော ဆုံးဖြတ်ချက်သစ်ပင်မှတပါး အခြားသော ဆုံးဖြတ်ချက် ကိရိယာများကိုလည်း သင်အသုံးပြုနိုင်ကြောင်း မှတ်သားထားသင့်သည်။ ဆုံးဖြတ်ချက် matrix သည် မတူညီသော စံနှုန်းများအတိုင်း ပြုလုပ်ရမည့် ဆုံးဖြတ်ချက်ကို အကဲဖြတ်ရန်အတွက် အလွန်လက်တွေ့ကျပြီး၊ ၎င်းကို မည်သို့လုပ်ဆောင်သည်ကို ကြည့်ရှုရန် အောက်ပါလင့်ခ်ကို နှိပ်ပါ။

ဆုံးဖြတ်ချက်သစ်ပင်၏ အားသာချက်များနှင့် အားနည်းချက်များ

အားသာချက်-

• ဆုံးဖြတ်ချက်သစ်ပင်များသည် နားလည်ရန်လွယ်ကူသည်။
• ဆုံးဖြတ်ချက်သစ်ပင်တစ်ခုသည် သင့်အား ဖြစ်နိုင်ခြေရှိသော အခြေအနေအားလုံးကို ကမ္ဘာနှင့်အဝှမ်း မြင်ယောင်နိုင်စေကာ အခြေအနေတစ်ခုစီတွင် မျှော်လင့်ထားသည့် ရလဒ်ကို မည်သို့မြင်နိုင်စေမည်နည်း။
• ဤပုံကြမ်းအမျိုးအစားသည် ဖန်တီးရန် အချိန်အများကြီးမယူသောကြောင့် အလွန်ထိရောက်သော်လည်း ပြီးမြောက်ရန် မြန်ဆန်ပါသည်။
• အကြံဉာဏ်သစ်များ သို့မဟုတ် ဇာတ်လမ်းပုံစံများကိုလည်း ရလဒ်သို့ ပေါင်းထည့်နိုင်ပြီး၊ ၎င်းကို လိုက်လျောညီထွေဖြစ်စေသော ဇယားကွက်တစ်ခုဖြစ်အောင် ပြုလုပ်နိုင်သည်။
• နောက်ဆုံးတွင်၊ ဆုံးဖြတ်ချက်သစ်ကို အခြားဆုံးဖြတ်ချက်ကိရိယာများနှင့် အလွယ်တကူ ပေါင်းစပ်နိုင်သည်။

အားနည်းချက်များ-

• ဆုံးဖြတ်ချက်သစ်ပင်တွင် ဆုံးဖြတ်ချက်အမှတ်များစွာ သို့မဟုတ် ဖြစ်နိုင်ခြေရှိသော အခြေအနေများစွာရှိပါက၊ ၎င်းသည် ရှုပ်ထွေးသောပုံစံတစ်ခု ဖြစ်လာနိုင်သည်။
• မကြာခဏဆိုသလို၊ အဖြစ်အပျက်တစ်ခုစီ၏ဖြစ်နိုင်ခြေကို အတိအကျ မဆုံးဖြတ်နိုင်သောကြောင့် တိကျမှုလည်း ဖြစ်နိုင်သည်။
• ဆုံးဖြတ်ချက်သစ်ပင်သည် ဆုံးဖြတ်ချက်ချသည့်ကိရိယာတစ်ခုမျှသာဖြစ်သော်လည်း နောက်ဆုံးဆုံးဖြတ်ချက်ကို တစ်စုံတစ်ဦးမှ ပြုလုပ်ရမည်ဖြစ်သည်။