Ti-84 ဂဏန်းတွက်စက်တွင် ပုံမှန်ဖြစ်နိုင်ခြေများကို တွက်ချက်နည်း

ပုံမှန် ဖြန့်ဖြူးမှုသည် စာရင်းဇယားအားလုံးတွင် အသုံးအများဆုံး ဖြန့်ဖြူးမှုဖြစ်သည်။ ဤသင်ခန်းစာတွင် TI-84 ဂဏန်းတွက်စက်ပေါ်တွင် အောက်ပါလုပ်ဆောင်ချက်များကို မည်သို့အသုံးပြုရကြောင်း ရှင်းပြသည်-

normalpdf(x, μ, σ) သည် ပုံမှန် pdf နှင့်ဆက်စပ်နေသည့် ဖြစ်နိုင်ခြေကို ပြန်ပေးသည်-

• x = တစ်ဦးချင်းတန်ဖိုး
• µ = လူဦးရေကို ဆိုလိုသည်။
• σ = လူဦးရေစံသွေဖည်

normalcdf(lower_x၊ upper_x၊ μ, σ) သည် တန်ဖိုးနှစ်ခုကြားရှိ ပုံမှန် cdf နှင့်ဆက်စပ်နေသော တိုးပွားလာနိုင်သည့် ဖြစ်နိုင်ခြေကို ပြန်ပေးသည်။

ရွှေ-

• lower_x = တစ်ဦးချင်းတန်ဖိုး နိမ့်သည်။
• upper_x = အထက်တစ်ဦးချင်းတန်ဖိုး
• µ = လူဦးရေကို ဆိုလိုသည်။
• σ = လူဦးရေစံသွေဖည်

ဤလုပ်ဆောင်ချက်နှစ်ခုကို 2nd ကိုနှိပ်ပြီး vars ကိုနှိပ်ခြင်းဖြင့် TI-84 ဂဏန်းတွက်စက်တွင် အသုံးပြုနိုင်သည်။ ၎င်းသည် သင့်အား normalpdf() နှင့် normalcdf() ကို သုံးနိုင်သည့် DISTR ဖန်သားပြင်သို့ ခေါ်ဆောင်သွားပါမည်။

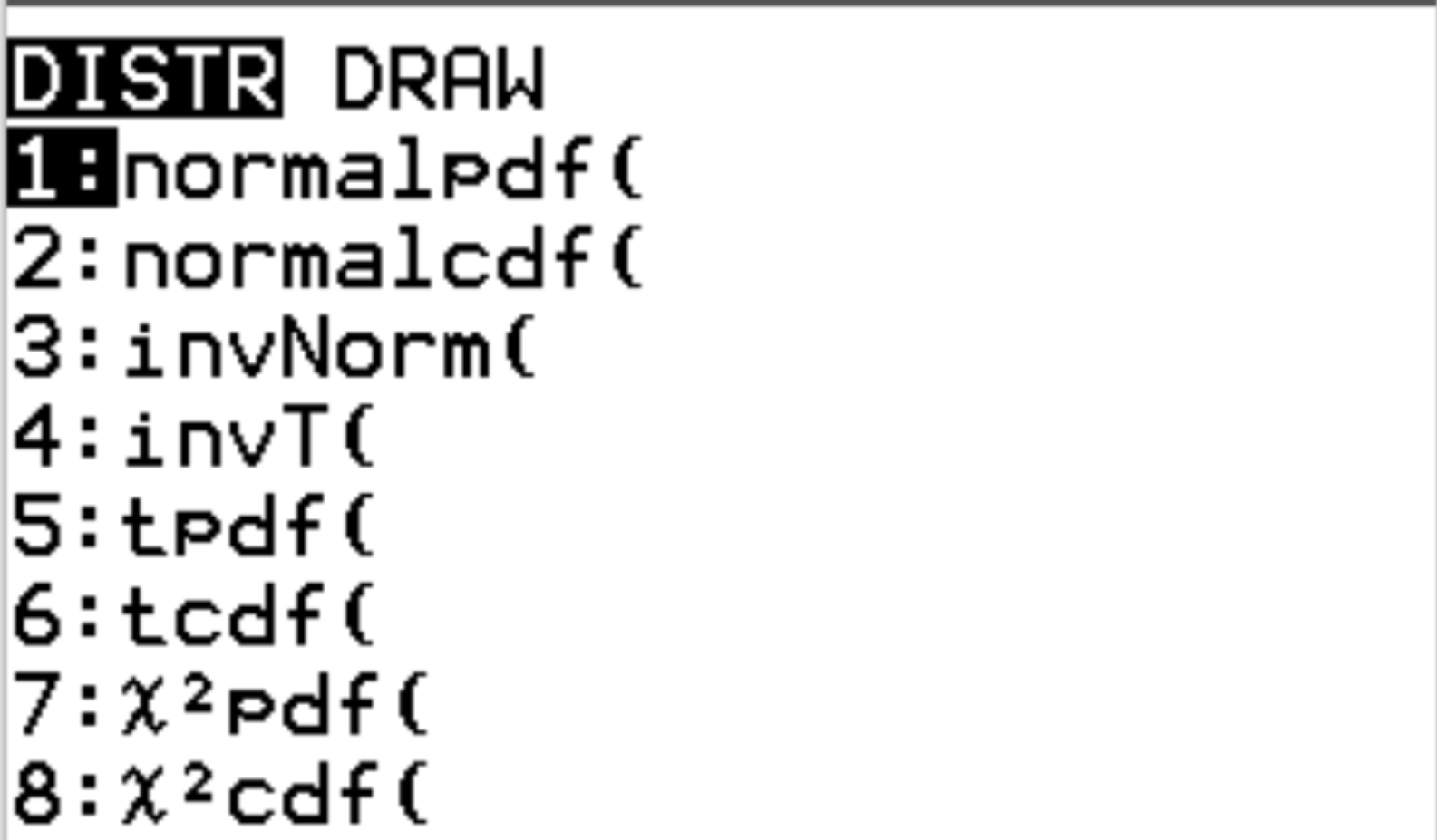
အောက်ပါဥပမာများသည် မတူညီသောမေးခွန်းများကိုဖြေဆိုရန် ဤလုပ်ဆောင်ချက်များကိုမည်သို့အသုံးပြုရပုံကိုဖော်ပြသည်။

ဥပမာ 1- x ထက် သာမာန်ဖြစ်နိုင်ခြေ

မေးခွန်း- ပျမ်းမျှ = 40 နှင့် စံသွေဖည် = 6 ဖြင့် ပုံမှန်ဖြန့်ဖြူးမှုအတွက်၊ တန်ဖိုး 45 ထက် ပိုများသည်ဟူသော ဖြစ်နိုင်ခြေကို ရှာပါ။

အဖြေ- normalcdf(x, 10000, μ, σ) လုပ်ဆောင်ချက်ကို အသုံးပြုပါ။

normalcdf(45၊ 10000၊ 40၊ 6) = 0.2023

မှတ်ချက်။

ဥပမာ 2- ပုံမှန်ဖြစ်နိုင်ခြေ x ထက်နည်းသည်။

မေးခွန်း- ပျမ်းမျှ = 100 နှင့် စံသွေဖည် = 11.3 ဖြင့် ပုံမှန်ဖြန့်ဖြူးမှုအတွက်၊ တန်ဖိုးသည် 98 ထက်နည်းသော ဖြစ်နိုင်ခြေကို ရှာပါ။

အဖြေ- normalcdf(-10000, x, μ, σ) လုပ်ဆောင်ချက်ကို အသုံးပြုပါ။

normalcdf(-10000၊ 98၊ 100၊ 11.3) = 0.4298

မှတ်ချက်။

ဥပမာ 3- တန်ဖိုးနှစ်ခုကြားတွင် ပုံမှန်ဖြစ်နိုင်ခြေ

မေးခွန်း- ပျမ်းမျှ = 50 နှင့် စံသွေဖည် = 4 ဖြင့် ပုံမှန်ဖြန့်ဖြူးမှုအတွက်၊ တန်ဖိုး 48 နှင့် 52 အကြား ဖြစ်နိုင်ခြေကို ရှာပါ။

အဖြေ- normalcdf(smaller_x, Larger_x, μ, σ) လုပ်ဆောင်ချက်ကို သုံးပါ။

normalcdf(48၊ 52၊ 50၊ 4) = 0.3829

ဥပမာ 4- တန်ဖိုးနှစ်ခုမှလွဲ၍ ပုံမှန်ဖြစ်နိုင်ခြေ

မေးခွန်း- ပျမ်းမျှ = 22 နှင့် စံသွေဖည် = 4 ဖြင့် ပုံမှန်ဖြန့်ဖြူးမှုအတွက်၊ တန်ဖိုးသည် 20 ထက်နည်းသော သို့မဟုတ် 24 ထက် ပိုများသည်ဟူသော ဖြစ်နိုင်ခြေကို ရှာပါ။

အဖြေ- function normalcdf(-10000၊ small_x, μ, σ) + normalcdf(larger_x, 10000, μ, σ) ကိုသုံးပါ။

normalcdf(-10000၊ 20၊ 22၊ 4) + normalcdf(24၊ 10000၊ 22၊ 4) = 0.6171