ပုံမှန်ဖြန့်ဖြူး

အားဖြင့် Benjamin Anderson ဩဂုတ် 3, 2023 ဖြစ်နိုင်ခြေ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် ကိန်းဂဏန်းစာရင်းအင်းများ တွင် ပုံမှန် ဖြန့်ဖြူးမှုအား ရှင်းပြထားသည်။ ထို့ကြောင့်၊ ပုံမှန်ဖြန့်ဖြူးခြင်း၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်၊ ပုံမှန်ဖြန့်ဝေမှုများ၏ ဥပမာများနှင့် ပုံမှန်ဖြန့်ဖြူးခြင်း၏ ဂုဏ်သတ္တိများကား အဘယ်နည်း။

သာမာန်ဖြန့်ဖြူးမှုကား အဘယ်နည်း။

ပုံမှန်ဖြန့်ဝေမှုသည် ဆက်တိုက်ဖြစ်နိုင်ခြေဖြန့်ဝေမှုတစ်ခုဖြစ်ပြီး ဂရပ်သည် ခေါင်းလောင်းပုံသဏ္ဌာန်ဖြစ်ပြီး ၎င်း၏ဆိုလိုရင်းနှင့်ပတ်သက်၍ အချိုးညီညီဖြစ်သည်။ ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ ပုံမှန်ဖြန့်ဖြူးမှုကို အလွန်ကွဲပြားသောလက္ခဏာများနှင့်အတူ နမူနာပုံစံပြုလုပ်ရန်အသုံးပြုသည်၊ ထို့ကြောင့် ဤဖြန့်ဝေမှုသည် အလွန်အရေးကြီးပါသည်။

တကယ်တော့၊ စာရင်းဇယားအရ၊ ပုံမှန်ဖြန့်ဖြူးမှုကို ဖြစ်နိုင်ခြေဖြန့်ဝေမှုအားလုံး၏ အရေးအကြီးဆုံး ဖြန့်ဖြူးမှုဟု ယူဆထားသောကြောင့် ၎င်းသည် လက်တွေ့ကမ္ဘာဖြစ်ရပ်များစွာကို စံနမူနာပြနိုင်ရုံသာမက ပုံမှန်ဖြန့်ဖြူးမှုကိုလည်း အခြားသော အမျိုးအစားများကို ခန့်မှန်းရန်အတွက်လည်း အသုံးပြုနိုင်သည်။ ဖြန့်ဖြူးမှုများ။ အချို့သောအခြေအနေများအောက်တွင်။

ပုံမှန်ဖြန့်ဝေမှုအတွက် သင်္ကေတသည် စာလုံးအကြီး N ဖြစ်သည်၊ ထို့ကြောင့်၊ ကိန်းရှင်တစ်ခုသည် ပုံမှန်ဖြန့်ဝေမှုနောက်သို့ လိုက်ကြောင်းညွှန်ပြရန်အတွက် ၎င်းကို အက္ခရာ N ဖြင့်ညွှန်ပြပြီး ၎င်း၏ဂဏန်းသင်္ချာပျမ်းမျှနှင့် စံသွေဖည်တန်ဖိုးများကို ကွင်းအတွင်းထည့်သွင်းထားသည်။

$X\sim N(\mu,\sigma)$

ပုံမှန်ဖြန့်ဖြူးမှုတွင် Gaussian ဖြန့်ဖြူးမှု ၊ Gaussian ဖြန့်ဖြူးမှု နှင့် Laplace-Gauss ဖြန့်ဖြူးမှု အပါအဝင် မတူညီသောအမည်များစွာရှိသည်။

ပုံမှန်ဖြန့်ဝေမှုများ၏ ဥပမာများ

ပုံမှန်အားဖြင့်၊ ပုံမှန်ဖြန့်ဝေမှုကို လိုက်နာသော ဒေတာအတွဲများတွင် လေ့လာတွေ့ရှိချက်အများအပြားပါရှိပြီး ယေဘုယျအကြောင်းအရာများကို အကျုံးဝင်ပါသည်။ အောက်တွင် ယေဘုယျအားဖြင့် သာမာန်ဖြန့်ဖြူးမှုဖြင့် စံနမူနာယူနိုင်သော ကိန်းဂဏန်းနမူနာများစွာ၏ ဥပမာများအောက်တွင် ရှိပါသည်။

ပုံမှန်ဖြန့်ဖြူးခြင်း၏ဥပမာများ-

သင်တန်းတစ်ခုတွင် ကျောင်းသားအရွယ်။
ကုမ္ပဏီဝန်ထမ်းတွေရဲ့ IQ။
စက်ရုံတစ်ရုံတွင် ချို့ယွင်းချက်ရှိသော အစိတ်အပိုင်းများကို တစ်ရက်လျှင် ထုတ်ပေးပါသည်။
သင်တန်းတစ်ခုတွင် ကျောင်းသားများ၏ စာမေးပွဲတွင် ရရှိသော အမှတ်များ။
စတော့အိတ်ချိန်းတွင် စာရင်းသွင်းထားသော ကုမ္ပဏီများ၏ အစုရှယ်ယာများ၏ အမြတ်ငွေ။

ပုံမှန်ဖြန့်ဝေဂရပ်

ပုံမှန် ဖြန့်ဖြူးမှု နှင့် ဤဖြစ်နိုင်ခြေ ဖြန့်ဖြူးမှု အမျိုးအစား အချို့ကို ကျွန်ုပ်တို့ မြင်ပြီးသည်နှင့်၊ သဘောတရားကို ပိုမိုနားလည်ရန် ၎င်း၏ ဂရပ်ပုံသည် မည်သို့ရှိပုံ ကို ကြည့်ကြပါစို့။

အောက်ပါဂရပ်တွင်၊ ပုံမှန်ဖြန့်ဖြူးမှု၏သိပ်သည်းဆလုပ်ဆောင်ပုံသည် ၎င်း၏ဂဏန်းသင်္ချာပျမ်းမျှတန်ဖိုးများနှင့် စံသွေဖည်မှုပေါ်မူတည်၍ မည်သို့ကွဲပြားသည်ကို သင်တွေ့မြင်နိုင်ပါသည်။

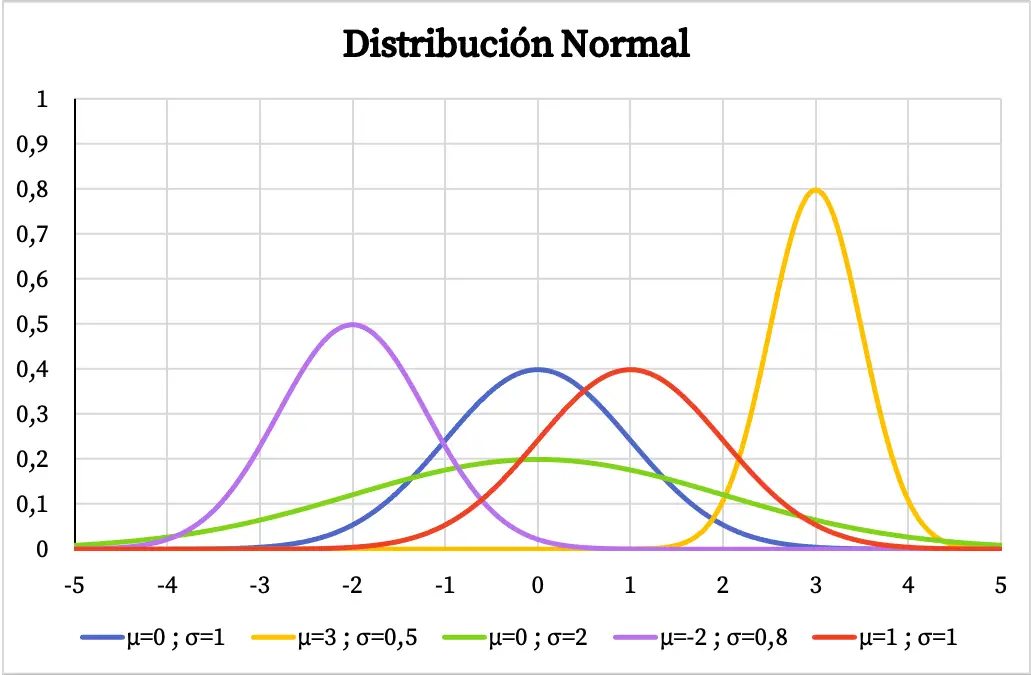
ဂဏန်းသင်္ချာဆိုလိုရင်းကို ဗဟိုပြုသော ခေါင်းလောင်းပုံသဏ္ဍာန်ရှိခြင်း၊ ကိန်းရှင်တစ်ခုတွင် ပုံမှန်ဖြန့်ဝေမှုရှိပါက ၎င်းသည် ထပ်ခါတလဲလဲ အများဆုံးတန်ဖိုးမှာ ပျမ်းမျှဖြစ်ပြီး ဆိုလိုရင်းတစ်ဝိုက်ရှိ တန်ဖိုးများသည် အလွန်အမင်းတန်ဖိုးများထက် မကြာခဏ ထပ်ခါထပ်ခါ ထပ်ခါထပ်ခါ ဖြစ်နေခြင်းကို ဆိုလိုပါသည်။ အလားတူ၊ ပုံမှန်ဖြန့်ဝေမှု၏ စံသွေဖည်မှု ကြီးမားလေ၊ ၎င်း၏ ဂရပ်ဖစ်ကိုယ်စားပြုပုံသဏ္ဍာန်ကို မြှောက်ပင့်ပေးသည်။

အခြားတစ်ဖက်တွင်၊ ပုံမှန်ဖြန့်ဖြူးမှု၏ တိုးပွားလာနိုင်သော ဖြစ်နိုင်ခြေလုပ်ဆောင်ချက်၏ ဂရပ်သည် ၎င်း၏ဂဏန်းသင်္ချာပျမ်းမျှနှင့် စံသွေဖည်မှုတန်ဖိုးများအပေါ်တွင် မူတည်သည်၊၊ သင်သည် အောက်ပါပုံတွင်တွေ့ရသကဲ့သို့၊

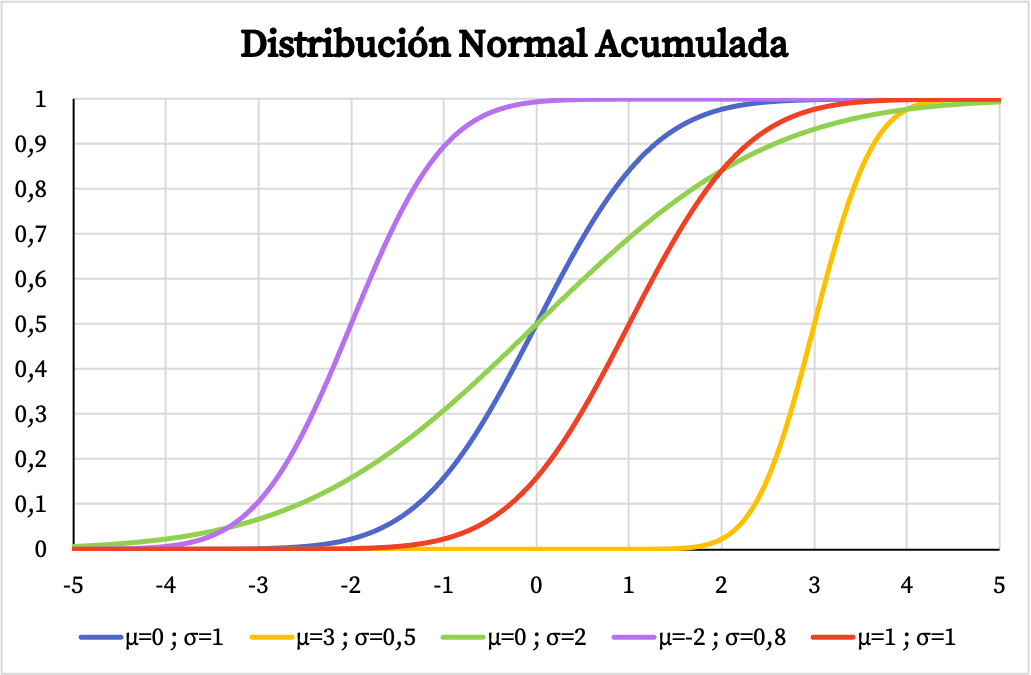
ပုံမှန်ဖြန့်ဖြူးမှု၏ စုစည်းဖြစ်နိုင်ခြေ လုပ်ဆောင်ချက်၏ ဂရပ်

သိပ်သည်းမှုလုပ်ဆောင်ချက်နှင့် ပုံမှန်ဖြန့်ဖြူးမှု၏ ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်သည် ဤဖြန့်ဖြူးမှုနှင့် ချိတ်ဆက်ထားသော ဖြစ်နိုင်ခြေများကို တွက်ချက်ရန် ဖြစ်နိုင်ချေရှိသည်။ သို့ရာတွင်၊ ၎င်းတို့၏ဖော်မြူလာများကို အသုံးပြုမည့်အစား၊ ၎င်းသည် ပိုမိုမြန်ဆန်သောကြောင့် ပုံမှန်ဖြန့်ဝေမှုဇယားများကို တိုက်ရိုက်အသုံးပြုနိုင်ပါသည်။ ဤဇယားများကို အောက်ပါလင့်ခ်တွင် တိုင်ပင်နိုင်ပါသည်။

➤ ပုံမှန် ဖြန့်ဖြူးမှုဇယားကို ကြည့်ပါ။

ပုံမှန်ဖြန့်ဖြူးခြင်း၏လက္ခဏာများ

ပုံမှန်ဖြန့်ဖြူးမှုတွင် အောက်ပါလက္ခဏာများ ရှိသည်။

ပုံမှန် ဖြန့်ဖြူးမှုသည် ၎င်း၏ ဂဏန်းသင်္ချာ ပျမ်းမျှ (μ) နှင့် ၎င်း၏ စံသွေဖည်မှု (σ) နှစ်ခုပေါ်တွင် မူတည်သည်။

$X\sim N(\mu,\sigma)$

ပုံမှန်ဖြန့်ဖြူးမှုသည် အပြုသဘောနှင့် အနုတ်တန်ဖိုးများကို ယူနိုင်သည်၊ ထို့ကြောင့် ပုံမှန်ဖြန့်ဖြူးမှု၏ဒိုမိန်းတွင် ကိန်းဂဏာန်းအစစ်အမှန်များပါဝင်သည်။

$x\in \mathbb{R}$

ပုံမှန်ဖြန့်ဝေမှု၏ ပျမ်းမျှနှင့် မုဒ်သည် ဖြန့်ဖြူးမှု၏ဂဏန်းသင်္ချာပျမ်းမျှနှင့် ညီမျှသည်။

$Me=Mo=\mu$

ပုံမှန်ဖြန့်ဖြူးမှု၏ skewness coefficient နှင့် kurtosis coefficient သည် သုညဖြစ်သည်။

$\begin{array}{c}A=0\\[2ex]C=0\end{array}$

ပုံမှန်ဖြန့်ဖြူးမှု၏သိပ်သည်းဆလုပ်ဆောင်မှုအတွက် ဖော်မြူလာမှာ-

$\displaystyle P[X=x]=\frac1{\sigma\sqrt{2\pi}}\; e^{ - \frac{(x-\mu)^2}{2\sigma^2}}$

အလားတူ၊ ပုံမှန်ဖြန့်ဝေမှု၏ တိုးပွားနိုင်ခြေရှိသော လုပ်ဆောင်ချက်အတွက် ဖော်မြူလာမှာ-

$\displaystyle P[X\leq x]=\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^x e^{-\frac{(x - \mu)^2}{2\sigma^2}}\, dx ,\quad x\in\mathbb{R}$

ဗဟိုကန့်သတ်သီအိုရီ၏ အသုံးချမှုတစ်ခုမှာ Poisson ဖြန့်ဝေမှု တစ်ခုသည် λ ၏တန်ဖိုးလုံလောက်စွာကြီးမားသောအခါတွင် ပုံမှန်ဖြန့်ဝေမှုကို ခန့်မှန်းနိုင်သည် ။

$\text{Poisson}(\lambda)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(\lambda, \sqrt{\lambda}\right)$

ဗဟိုကန့်သတ်သီအိုရီ၏နောက်ထပ်အသုံးချမှုမှာ ကိန်းဂဏန်း ပမာဏများစွာဖြင့် ဒေတာအတွဲများအတွက် ပုံမှန်ဖြန့်ဝေမှုဖြင့် အနီးစပ်ဆုံးဖြစ်နိုင်သည်။

$\text{Bin}(n,p)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(n\cdot p, \sqrt{n\cdot p \cdot (1-p)}\right)$

စံပုံမှန် ဖြန့်ဖြူးမှု

စံပုံမှန်ဖြန့်ဖြူးမှု ယူနစ်ပုံမှန်ဖြန့်ဝေမှု ဟုလည်း ခေါ်သည်၊ ပုံမှန်ဖြန့်ဝေမှု၏ အရိုးရှင်းဆုံးကိစ္စဖြစ်သည်။ ပို၍တိကျသည်မှာ၊ စံပုံမှန်ဖြန့်ဖြူးမှုသည် ပျမ်းမျှနှင့်စံသွေဖည်တန်ဖိုးများ 0 နှင့် 1 အသီးသီးရှိသော ပုံမှန်ဖြန့်ဖြူးမှုတစ်ခုဖြစ်သည်။

$\displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}$

စာရိုက်ခြင်းဟုခေါ်သော လုပ်ငန်းစဉ်ကိုအသုံးပြုခြင်းဖြင့် ပုံမှန်ဖြန့်ဖြူးမှုတစ်ခုအား စံပုံမှန်ဖြန့်ဝေမှုအဖြစ်သို့ ပြောင်းလဲနိုင်သည်၊ ၎င်းသည် ၎င်း၏ဂဏန်းသင်္ချာပျမ်းမျှတန်ဖိုးတစ်ခုစီမှ ဂဏန်းသင်္ချာကိုနုတ်ပြီး ၎င်း၏စံသွေဖည်မှုဖြင့် ပိုင်းခြားခြင်းကို သတိပြုပါ။

ထို့အပြင်၊ စံပုံမှန်ဖြန့်ဝေမှုကို ၎င်း၏ဖြစ်နိုင်ခြေဇယားကို အသုံးပြု၍ ပုံမှန်ဖြန့်ဖြူးမှု၏ဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ရန် အသုံးပြုသည်။ ထို့ကြောင့်၊ ပုံမှန်ဖြန့်ဖြူးမှုတစ်ခု၏ဖြစ်နိုင်ခြေကိုရှာဖွေရန်၊ variable သည် ၎င်းကို standard normal distribution အဖြစ်သို့ပြောင်းလဲရန် ဦးစွာထည့်သွင်းပြီး ဆက်စပ်ဖြစ်နိုင်ခြေတန်ဖိုးကိုကြည့်ရန် ဇယားကိုကြည့်ရှုပါ။ ပိုမိုသိရှိလိုပါက အောက်ပါလင့်ခ်ကိုနှိပ်ပါ။

➤ Standard Normal Distribution ကို ကြည့်ပါ။

သာမာန် ဖြန့်ဖြူးမှုနှင့် အင်ပါယာ အုပ်ချုပ်မှု

စာရင်းဇယားများတွင် လက်မ၏စည်းမျဉ်း ၊ 68-95-99.7 စည်းမျဉ်း ဟုလည်း ခေါ်သည် ၊ သည် ပုံမှန်ဖြန့်ဝေမှုတစ်ခုတွင် တန်ဖိုးများ၏ ရာခိုင်နှုန်းများကို သတ်မှတ်ပေးသည့် စည်းမျဉ်းတစ်ခုဖြစ်သည်။

ပို၍ တိကျသည်မှာ လက်မ၏ စည်းကမ်းသည် အောက်ပါတို့ကို ဖော်ပြသည်။

ပုံမှန်ဖြန့်ဖြူးမှုတစ်ခုရှိ တန်ဖိုးများ၏ 68% သည် ဆိုလိုရင်း၏ စံသွေဖည်မှုတစ်ခုအတွင်းတွင် ရှိနေသည်။
ပုံမှန်ဖြန့်ဖြူးမှုတစ်ခုရှိ တန်ဖိုးများ၏ 95% သည် ဆိုလိုရင်း၏ စံသွေဖီမှုနှစ်ခုအတွင်း တည်ရှိနေသည်။
ပုံမှန်ဖြန့်ဖြူးမှုတစ်ခုရှိ တန်ဖိုးများ၏ 99.7% သည် ဆိုလိုခြင်း၏စံသွေဖည်မှုသုံးမျိုးအတွင်း ကျရောက်သည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။