ပြီးပြည့်စုံသော multicollinearity ဆိုသည်မှာ အဘယ်နည်း။ (အဓိပ္ပါယ်နှင့် ဥပမာများ)

စာရင်းဇယားများတွင်၊ ကိန်းဂဏန်းနှစ်ခု သို့မဟုတ် နှစ်ခုထက်ပိုသော ခန့်မှန်းနိုင်သောကိန်းရှင်များသည် တစ်ခုနှင့်တစ်ခု အလွန်ဆက်စပ်နေသောအခါ၊ ၎င်းတို့သည် ဆုတ်ယုတ်မှုပုံစံတွင် ထူးခြားသော သို့မဟုတ် အမှီအခိုကင်းသော အချက်အလက်များကို ပေးစွမ်းနိုင်ခြင်း မရှိသည့်အခါတွင် ကိန်းဂဏန်းများ ပေါင်းစပ် ဖြစ်ပေါ်မှု ဖြစ်ပေါ်သည်။

ကိန်းရှင်များကြားတွင် ဆက်စပ်ဆက်စပ်မှုဒီဂရီသည် လုံလောက်စွာမြင့်မားပါက၊ ၎င်းသည် ဆုတ်ယုတ်မှုပုံစံကို အံဝင်ခွင်ကျဖြစ်စေပြီး အနက်ပြန်ဆိုရာတွင် ပြဿနာများဖြစ်စေနိုင်သည်။

Multicollinearity ၏ အဆိုးရွားဆုံးဖြစ်ရပ်ကို perfect multicollinearity ဟုခေါ်သည်။ ကြိုတင်ခန့်မှန်းကိန်းရှင် နှစ်ခု သို့မဟုတ် ထို့ထက်ပိုသော ကိန်းရှင်များသည် တစ်ခုနှင့်တစ်ခု တိကျသော linear ဆက်နွယ်မှုရှိသောအခါ ၎င်းသည် ဖြစ်ပေါ်သည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့တွင် အောက်ပါဒေတာအစုံရှိသည်ဆိုပါစို့။

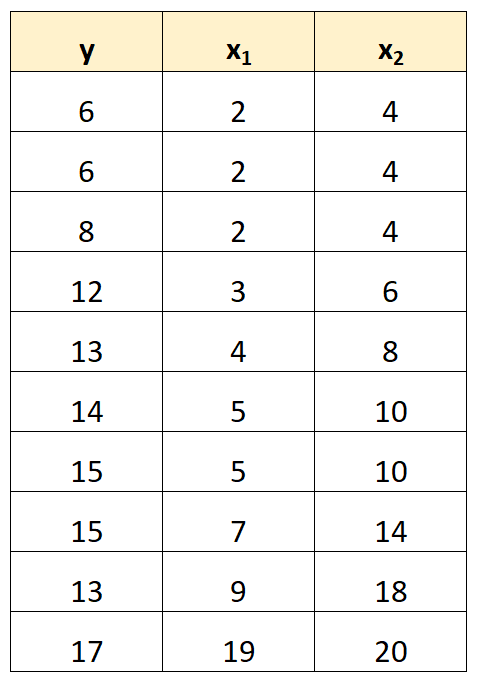
ခန့်မှန်းသူ variable x ₂ ၏တန်ဖိုးများသည် ရိုးရိုး x ₁ ၏တန်ဖိုးများကို 2 ဖြင့်မြှောက်ကြောင်းသတိပြုပါ။

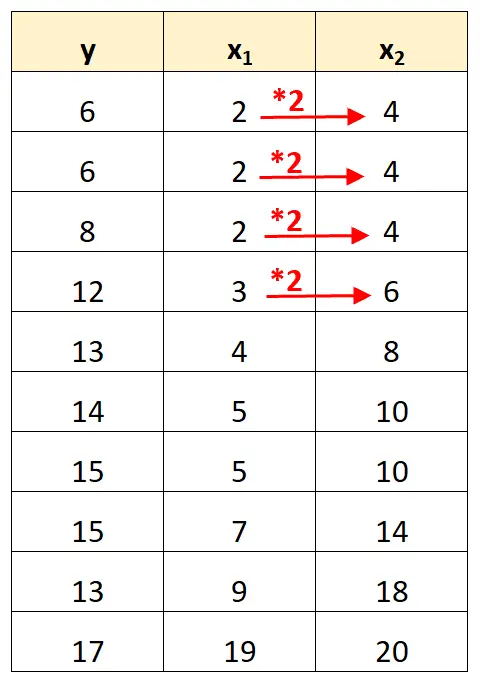
ဤသည်မှာ ပြီးပြည့်စုံသော multicollinearity ၏ ဥပမာတစ်ခုဖြစ်သည်။

ပြီးပြည့်စုံသော multicollinearity ပြဿနာ

ဒေတာအတွဲတစ်ခုတွင် ပြီးပြည့်စုံသော multicollinearity ရှိနေသောအခါ၊ သာမန် အနည်းဆုံးစတုရန်းများသည် ဆုတ်ယုတ်မှုကိန်းဂဏန်းများ၏ ခန့်မှန်းချက်များကို မထုတ်ပေးနိုင်ပါ။

အမှန်မှာ၊ _{x 2} သည် x ₁ ရွေ့လျားသည့်အခါ အမြဲအတိအကျ ရွေ့လျားနေချိန်တွင် တုံ့ပြန်မှုကိန်းရှင် (y) ပေါ်ရှိ ကြိုတင်ခန့်မှန်းကိန်းရှင် (x ₁ ) ၏ မဖြစ်စလောက်အကျိုးသက်ရောက်မှုကို ခန့်မှန်းရန် မဖြစ်နိုင်ပေ။

အတိုချုပ်အားဖြင့်၊ ပြီးပြည့်စုံသော multicollinearity သည် regression model တစ်ခုစီရှိ coefficient တစ်ခုစီအတွက် တန်ဖိုးကို ခန့်မှန်းရန် မဖြစ်နိုင်ပေ။

ပြီးပြည့်စုံသော multicollinearity ကိုမည်သို့ကိုင်တွယ်မည်နည်း။

ပြီးပြည့်စုံသော multicollinearity ကိုကိုင်တွယ်ရန် အရိုးရှင်းဆုံးနည်းလမ်းမှာ အခြားကိန်းရှင်နှင့် အတိအကျ linear ဆက်နွယ်မှုရှိသော variable များကို ဖယ်ရှားရန်ဖြစ်သည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့၏ယခင်ဒေတာအတွဲတွင်၊ ကျွန်ုပ်တို့သည် x _{2 ကို} ကြိုတင်ခန့်မှန်းနိုင်သောကိန်းရှင်အဖြစ် ရိုးရှင်းစွာဖယ်ရှားနိုင်သည်။

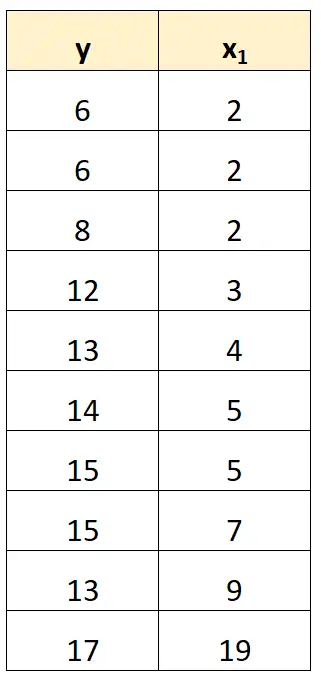
ထို့နောက် ကျွန်ုပ်တို့သည် x _{1 ကို} ခန့်မှန်းသည့်ကိန်းရှင်အဖြစ်နှင့် တုံ့ပြန်မှုကိန်းရှင်အဖြစ် y ကိုအသုံးပြု၍ ဆုတ်ယုတ်မှုပုံစံတစ်ခုကို ဖြည့်သွင်းမည်ဖြစ်သည်။

ပြီးပြည့်စုံသော multicollinearity နမူနာများ

အောက်ဖော်ပြပါ ဥပမာများသည် လက်တွေ့တွင် ပြီးပြည့်စုံသော multicollinearity ၏ အဖြစ်အများဆုံး မြင်ကွင်းသုံးခုကို ပြသထားသည်။

1. ကြိုတင်ခန့်မှန်းကိန်းရှင်သည် အခြားတစ်ခု၏ ဆတိုးကိန်းတစ်ခုဖြစ်သည်။

အချို့သော လင်းပိုင်မျိုးစိတ်များ၏ အလေးချိန်ကို ခန့်မှန်းရန် “ အမြင့် စင်တီမီတာ” နှင့် “ အမြင့် မီတာ” ကို အသုံးပြုလိုသည် ဆိုကြပါစို့။

ဤအရာသည် ကျွန်ုပ်တို့၏ဒေတာအတွဲကဲ့သို့ ဖြစ်ကောင်းဖြစ်နိုင်သည်-

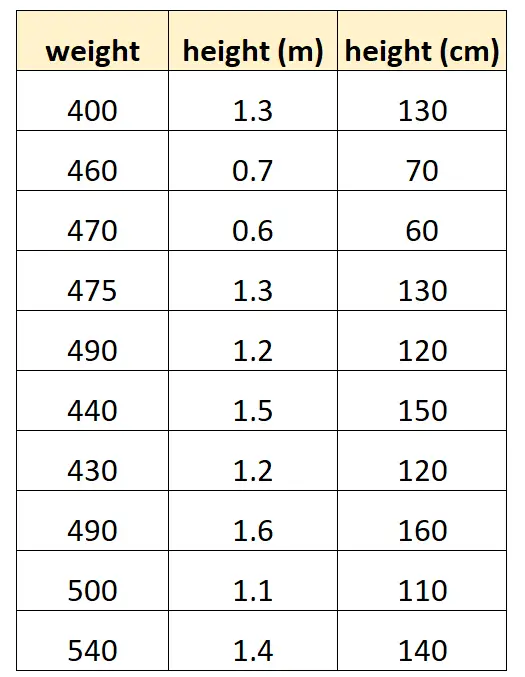
“ အမြင့် စင်တီမီတာ” ၏ တန်ဖိုးသည် 100 ဖြင့် မြှောက်ထားသော “ အမြင့် မီတာ” နှင့် ညီမျှကြောင်း သတိပြုပါ။ ၎င်းသည် ပြီးပြည့်စုံသော multicollinearity တစ်ခုဖြစ်သည်။

ဤဒေတာအတွဲကိုအသုံးပြု၍ R တွင် မျဉ်းဖြောင့်ဆုတ်ယုတ်မှုပုံစံကို အံဝင်ခွင်ကျဖြစ်အောင် ကျွန်ုပ်တို့ကြိုးစားပါက၊ ခန့်မှန်းသူကိန်းရှင် “ မီတာ” အတွက် ကိန်းဂဏန်းခန့်မှန်းချက်ကို ထုတ်ပြန်နိုင်မည် မဟုတ်ပါ။

 #define data
df <- data. frame (weight=c(400, 460, 470, 475, 490, 440, 430, 490, 500, 540),
                 m=c(1.3, .7, .6, 1.3, 1.2, 1.5, 1.2, 1.6, 1.1, 1.4),
                 cm=c(130, 70, 60, 130, 120, 150, 120, 160, 110, 140))

#fit multiple linear regression model
model <- lm(weight~m+cm, data=df)

#view summary of model
summary(model)

Call:
lm(formula = weight ~ m + cm, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-70,501 -25,501 5,183 19,499 68,590 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 458,676 53,403 8,589 2.61e-05 ***
m 9.096 43.473 0.209 0.839    
cm NA NA NA NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 41.9 on 8 degrees of freedom
Multiple R-squared: 0.005442, Adjusted R-squared: -0.1189 
F-statistic: 0.04378 on 1 and 8 DF, p-value: 0.8395

2. ကြိုတင်ခန့်မှန်းကိန်းရှင်သည် အခြားတစ်ခု၏ အသွင်ပြောင်းဗားရှင်းဖြစ်သည်။

ဘတ်စကတ်ဘောကစားသမားများ၏ အဆင့်သတ်မှတ်ချက်ကို ခန့်မှန်းရန် “ အမှတ်များ” နှင့် “ စကေးရမှတ်များ” ကို အသုံးပြုလိုသည်ဆိုပါစို့။

မပြောင်းလဲနိုင်သော “စကေးရမှတ်များ” ကို အောက်ပါအတိုင်း တွက်ချက်သည်ဆိုပါစို့။

အတိုင်းအတာမှတ်များ = (အမှတ် – µ _{အမှတ်များ} ) / σ _{မှတ်များ}

ဤအရာသည် ကျွန်ုပ်တို့၏ဒေတာအတွဲကဲ့သို့ ဖြစ်ကောင်းဖြစ်နိုင်သည်-

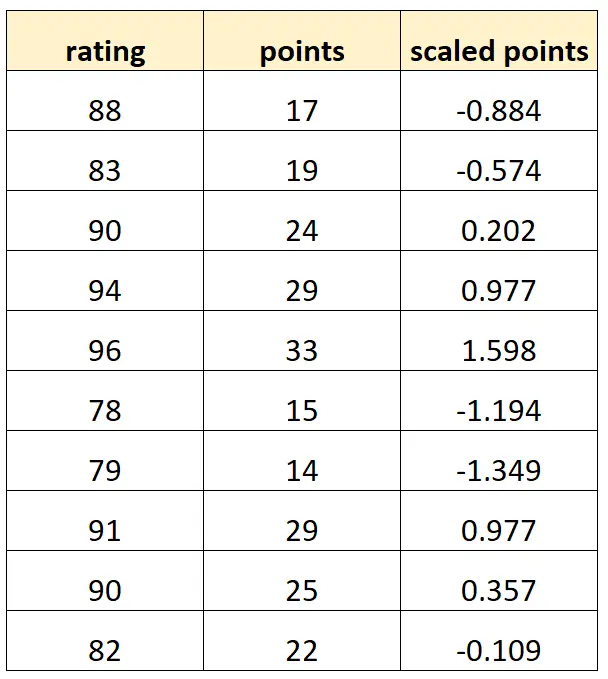
“ စကေးချထားသော အမှတ်များ” တန်ဖိုးတစ်ခုစီသည် ရိုးရိုး “ အမှတ်များ” ၏ စံဗားရှင်းတစ်ခုဖြစ်ကြောင်း သတိပြုပါ။ ဤသည်မှာ ပြီးပြည့်စုံသော multicollinearity ဖြစ်သည်။

ဤဒေတာအတွဲကိုအသုံးပြု၍ R တွင် မျဉ်းဖြောင့်ဆုတ်ယုတ်မှုပုံစံကို အံဝင်ခွင်ကျဖြစ်အောင် ကြိုးစားပါက၊ “ စကေးချထားသော အမှတ်များ” ကိန်းရှင်ကိန်းရှင်အတွက် ကိန်းဂဏန်းခန့်မှန်းချက်ကို ထုတ်လုပ်နိုင်မည်မဟုတ်ပါ-

 #define data
df <- data. frame (rating=c(88, 83, 90, 94, 96, 78, 79, 91, 90, 82),
                 pts=c(17, 19, 24, 29, 33, 15, 14, 29, 25, 22))

df$scaled_pts <- (df$pts - mean(df$pts)) / sd(df$pts)

#fit multiple linear regression model
model <- lm(rating~pts+scaled_pts, data=df)

#view summary of model
summary(model)

Call:
lm(formula = rating ~ pts + scaled_pts, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-4.4932 -1.3941 -0.2935 1.3055 5.8412 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 67.4218 3.5896 18.783 6.67e-08 ***
pts 0.8669 0.1527 5.678 0.000466 ***
scaled_pts NA NA NA NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.953 on 8 degrees of freedom
Multiple R-squared: 0.8012, Adjusted R-squared: 0.7763 
F-statistic: 32.23 on 1 and 8 DF, p-value: 0.0004663

3. dummy ပြောင်းလဲနိုင်သော ထောင်ချောက်

ပြီးပြည့်စုံသော multicollinearity ဖြစ်ပေါ်နိုင်သည့်နောက်ထပ် ဇာတ်လမ်းကို dummy variable trap ဟုခေါ်သည်။ ဆုတ်ယုတ်မှုပုံစံတစ်ခုတွင် categorical variable တစ်ခုကိုယူ၍ 0၊ 1၊ 2 စသည်ဖြင့် တန်ဖိုးများကို ယူဆောင်သည့် “ dummy variable” သို့ ပြောင်းလိုသောအခါ၊

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် ၀င်ငွေကိုခန့်မှန်းရန် ခန့်မှန်းနိုင်သောကိန်းရှင် “ အသက်” နှင့် “ အိမ်ထောင်ရေးအခြေအနေ” ကိုအသုံးပြုလိုသည်ဆိုကြပါစို့။

“ အိမ်ထောင်ရေးအခြေအနေ” ကို ကြိုတင်ခန့်မှန်းနိုင်သောကိန်းရှင်အဖြစ် အသုံးပြုရန်၊ ၎င်းကို အရုပ်ပြောင်းကိန်းအဖြစ် ဦးစွာပြောင်းလဲရပါမည်။

ထိုသို့လုပ်ဆောင်ရန်၊ ကျွန်ုပ်တို့သည် “ Single” ကို အခြေခံတန်ဖိုးအဖြစ် ထားခဲ့နိုင်ပြီး၊ 0 သို့မဟုတ် 1 တန်ဖိုးများကို အောက်ပါအတိုင်း “ အိမ်ထောင်သည်” နှင့် “ ကွာရှင်းခြင်း” သို့ သတ်မှတ်ပေးသောကြောင့်၊

အမှားတစ်ခုသည် အောက်ပါအတိုင်း dummy variable သုံးခုကို ဖန်တီးရန် မှားယွင်းနေလိမ့်မည် ။

ဤကိစ္စတွင်၊ “ Single” variable သည် “ အိမ်ထောင်သည်” နှင့် “ ကွာရှင်းပြတ်စဲခြင်း” variable များ၏ ပြီးပြည့်စုံသော linear ပေါင်းစပ်မှုတစ်ခုဖြစ်သည်။ ဤသည်မှာ ပြီးပြည့်စုံသော multicollinearity ၏ ဥပမာတစ်ခုဖြစ်သည်။

ဤဒေတာအတွဲကို အသုံးပြု၍ R တွင် မျဉ်းကြောင်းပြန်ဆုတ်မှုပုံစံ အများအပြားကို အံဝင်ခွင်ကျဖြစ်အောင် ကျွန်ုပ်တို့ကြိုးစားပါက၊ ခန့်မှန်းသူကိန်းရှင်တစ်ခုစီအတွက် ကိန်းဂဏန်းခန့်မှန်းချက်ကို ကျွန်ုပ်တို့ ထုတ်လုပ်နိုင်မည်မဟုတ်ပါ-

 #define data
df <- data. frame (income=c(45, 48, 54, 57, 65, 69, 78, 83, 98, 104, 107),
                 age=c(23, 25, 24, 29, 38, 36, 40, 59, 56, 64, 53),
                 single=c(1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0),
                 married=c(0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1),
                 divorced=c(0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0))

#fit multiple linear regression model
model <- lm(income~age+single+married+divorced, data=df)

#view summary of model
summary(model)

Call:
lm(formula = income ~ age + single + married + divorced, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-9.7075 -5.0338 0.0453 3.3904 12.2454 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)   
(Intercept) 16.7559 17.7811 0.942 0.37739   
age 1.4717 0.3544 4.152 0.00428 **
single -2.4797 9.4313 -0.263 0.80018   
married NA NA NA NA   
divorced -8.3974 12.7714 -0.658 0.53187   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 8.391 on 7 degrees of freedom
Multiple R-squared: 0.9008, Adjusted R-squared: 0.8584 
F-statistic: 21.2 on 3 and 7 DF, p-value: 0.0006865

ထပ်လောင်းအရင်းအမြစ်များ

Regression ရှိ Multicollinearity နှင့် VIF အတွက်လမ်းညွှန်
R ဖြင့် VIF တွက်နည်း
Python တွင် VIF တွက်နည်း
Excel တွင် VIF တွက်ချက်နည်း