ဖြစ်နိုင်ခြေ လုပ်ဆောင်ချက်

အားဖြင့် Benjamin Anderson ဩဂုတ် 5, 2023 ဖြစ်နိုင်ခြေ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် ဖြစ်နိုင်ခြေရှိသော လုပ်ဆောင်ချက်များကို ရှင်းပြထားသည်။ ထို့ကြောင့်၊ ဖြစ်နိုင်ခြေ လုပ်ဆောင်ချက်၏ အဓိပ္ပါယ်၊ ၎င်း၏ ဂုဏ်သတ္တိများနှင့် ဖြစ်နိုင်ခြေ လုပ်ဆောင်ချက်ကို တွက်ချက်ခြင်း၏ ခိုင်မာသော ဥပမာတစ်ခုကို သင်တွေ့လိမ့်မည်။ ထို့အပြင် ဖြစ်နိုင်ခြေရှိသော လုပ်ဆောင်ချက်နှင့် အခြားဖြစ်နိုင်ခြေရှိသော လုပ်ဆောင်ချက်အမျိုးအစားများကြား ခြားနားချက်များကို တင်ပြထားသည်။

ဖြစ်နိုင်ခြေလုပ်ဆောင်ချက်ကဘာလဲ။

ဖြစ်နိုင်ခြေရှိသော လုပ်ဆောင်ချက် တစ်ခု၊ ဖြစ်နိုင်ခြေအစုလိုက်အပြုံလိုက် လုပ်ဆောင်ချက် ဟုလည်း ခေါ်သည် ၊ သည် အချို့သောတန်ဖိုးတစ်ခုပေါ်တွင် သီးခြားကျပန်းကိန်းရှင်တစ်ခု၏ဖြစ်နိုင်ခြေကို ဖော်ပြသည့် သင်္ချာလုပ်ဆောင်ချက်တစ်ခုဖြစ်သည်။

ဆိုလိုသည်မှာ၊ ဖြစ်နိုင်ခြေ လုပ်ဆောင်ချက်သည် တန်ဖိုးတစ်ခုနှင့် အတိအကျ တန်းတူဖြစ်ခြင်း၏ သီးခြားကိန်းရှင်တစ်ခုနှင့် ဆက်စပ်နေသော ဖြစ်နိုင်ခြေကို ပြန်ပေးသည်။

$f(x)=P[X=x]$

ဥပမာအားဖြင့်၊ အသေတစ်ခုအား လှိမ့်သည့်အခါ မည်သည့်ဂဏန်းမျှလှိမ့်နိုင်ခြေသည် 1/6 (အံတစ်ခုတွင် ဘက်ခြောက်ခုပါရှိသည်)၊ ထို့ကြောင့် ဤနမူနာနေရာနှင့်ဆက်စပ်သည့် ဖြစ်နိုင်ခြေလုပ်ဆောင်ချက်သည် မည်သည့်တန်ဖိုးအတွက်မဆို 1/6 နှင့် ညီမျှမည်ဖြစ်သည်။

ဖြစ်နိုင်ခြေ လုပ်ဆောင်ချက်၏ ဂုဏ်သတ္တိများ

ဖြစ်နိုင်ခြေ လုပ်ဆောင်ချက်များတွင် အောက်ပါ ဂုဏ်သတ္တိများ ရှိသည်။

ဖြစ်နိုင်ခြေသည် အနှုတ်မဖြစ်နိုင်ပါ၊ ထို့ကြောင့် ဖြစ်နိုင်ခြေလုပ်ဆောင်ချက်သည် x ၏တန်ဖိုးတိုင်းအတွက် သုည သို့မဟုတ် အပေါင်းဖြစ်သည်။

$f(x)\geq 0$

အလားတူ၊ ဖြစ်နိုင်ခြေအများဆုံးမှာ စည်းလုံးညီညွတ်မှုဖြစ်ပြီး၊ အဖြစ်အပျက်သည် အမြဲဖြစ်ပေါ်နေမည်ဟု ဆိုလိုသည်။ ထို့ကြောင့် ဖြစ်နိုင်ခြေလုပ်ဆောင်ချက်၏ အမြင့်ဆုံးတန်ဖိုးသည် 1 နှင့် ညီမျှသည်။

$f(x)\leq 1$

နောက်ဆုံးတွင်၊ ဖြစ်နိုင်ခြေလုပ်ဆောင်ချက်တစ်ခု၏တန်ဖိုးများအားလုံး၏ပေါင်းလဒ်သည် 1 ကိုပေးသည်၊ အဘယ်ကြောင့်ဆိုသော်၎င်းသည်နမူနာနေရာရှိဖြစ်နိုင်ခြေအားလုံး၏ပေါင်းလဒ်ဖြစ်သောကြောင့်ဖြစ်သည်။

$\displaystyle \sum_{i=1}^{+\infty}f(x_i)=\sum_{i=1}^{+\infty}p_i=1$

ဖြစ်နိုင်ခြေ လုပ်ဆောင်ချက် နမူနာ

ဖြစ်နိုင်ခြေလုပ်ဆောင်ချက်၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ဝိသေသလက္ခဏာများကို ယခုကျွန်ုပ်တို့သိပြီးဖြစ်နိုင်ချေရှိသော လုပ်ဆောင်ချက်အမျိုးအစား၏ ဥပမာကို ကြည့်ကြပါစို့။

သီးခြားအကြွေစေ့လေးခေါက်ပြုလုပ်ခြင်းဖြင့် 0၊ 1၊ 2၊ 3 နှင့် 4 ကြိမ်တွင် ဦးခေါင်းများရရှိရန် ဖြစ်နိုင်ခြေများကို တွက်ချက်ပါ။ ထို့နောက် ဖြစ်နိုင်ခြေရှိသော လုပ်ဆောင်ချက်ကို တွေ့ရှိကြောင်း ဂရပ်ပြပါ။

ပထမဦးစွာ၊ ကျွန်ုပ်တို့သည် ဦးခေါင်းရယူခြင်း၏ဖြစ်နိုင်ခြေများကိုတွက်ချက်ရမည်ဖြစ်ပြီး၊ ထိုသို့လုပ်ဆောင်ရန်၊ ဖြစ်နိုင်ခြေအမှုများကိုအမှုပေါင်းစုစုပေါင်းအရေအတွက်ဖြင့်ပိုင်းခြားရမည်ဖြစ်သည်။ အောက်ပါဇယားတွင် ဖြစ်နိုင်ခြေအားလုံးကို တွက်ချက်ကြည့်ရှုနိုင်သည်-

ဖြစ်နိုင်ခြေအားလုံးကို ကျွန်ုပ်တို့ တွက်ချက်ပြီးသည်နှင့်၊ ဂရပ်တစ်ခုပေါ်တွင် ဖြစ်နိုင်ခြေရှိသော လုပ်ဆောင်မှု၏ တန်ဖိုးများကို ကိုယ်စားပြုနိုင်သည်-

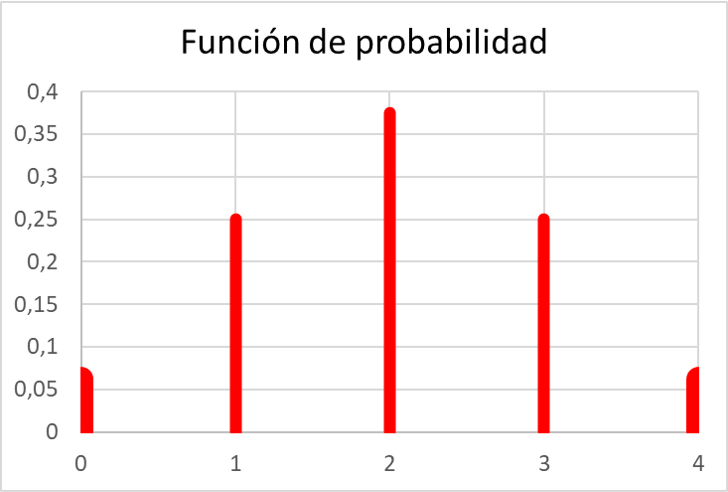
သင်တွေ့မြင်ရသည့်အတိုင်း၊ လေ့ကျင့်ခန်းရှိ ဖြစ်နိုင်ခြေရှိသောလုပ်ဆောင်ချက်သည် ၎င်း၏တန်ဖိုးများအားလုံး 0 နှင့် 1 အကြားရှိသောကြောင့် ၎င်းအပြင် ၎င်း၏တန်ဖိုးများအားလုံး၏ပေါင်းလဒ်သည် 1 နှင့် ညီမျှပါသည်။

ဖြစ်နိုင်ခြေ လုပ်ဆောင်ချက်နှင့် သိပ်သည်းမှု လုပ်ဆောင်ချက်

ဤကဏ္ဍတွင် ဖြစ်နိုင်ခြေလုပ်ဆောင်ချက်နှင့် သိပ်သည်းဆလုပ်ဆောင်မှုအကြား ခြားနားချက်ကို မြင်တွေ့ရမည်ဖြစ်ပြီး ၎င်းတို့သည် ရည်ရွယ်ချက်တူသော်လည်း မတူညီသောကိစ္စများတွင် အသုံးပြုသည့် ဖြစ်နိုင်ခြေရှိသည့် လုပ်ဆောင်ချက်နှစ်မျိုးဖြစ်သောကြောင့် ၎င်းတို့ကို တွေ့ရှိရမည်ဖြစ်သည်။

ဖြစ်နိုင်ခြေ လုပ်ဆောင်ချက် နှင့် သိပ်သည်းဆ လုပ်ဆောင်ချက် အကြား ခြားနားချက်မှာ ဖြစ်နိုင်ခြေ ဖော်ပြသည့် variable အမျိုးအစား ဖြစ်သည်။ စဉ်ဆက်မပြတ်ကိန်းရှင်တစ်ခု၏ ဖြစ်နိုင်ခြေများကို သတ်မှတ်ရန် သိပ်သည်းဆလုပ်ဆောင်ချက်ကို အသုံးပြုပြီး ဖြစ်နိုင်ခြေရှိသော လုပ်ဆောင်ချက်ကို သီးခြားကိန်းရှင်တစ်ခု၏ ဖြစ်နိုင်ခြေများကို သတ်မှတ်ရန် အသုံးပြုသည်။

ထို့ကြောင့်၊ variable ပေါ်မူတည်၍ probability function သို့မဟုတ် density function ကိုအသုံးပြုသည်။

သိပ်သည်းဆလုပ်ဆောင်မှုအကြောင်း ပိုမိုလေ့လာရန်၊ အောက်ပါလင့်ခ်ကို နှိပ်ပါ။

➤ ဖြစ်နိုင်ခြေသိပ်သည်းဆ လုပ်ဆောင်ချက်ကို ကြည့်ပါ။

ဖြစ်နိုင်ခြေ လုပ်ဆောင်ချက်နှင့် ဖြန့်ဖြူးရေး လုပ်ဆောင်ချက်

ဖြစ်နိုင်ခြေ လုပ်ဆောင်ချက် နှင့် ဖြန့်ဝေမှု လုပ်ဆောင်ချက် အကြား ခြားနားချက် မှာ ၎င်းတို့ သတ်မှတ်ထားသော ဖြစ်နိုင်ခြေ အမျိုးအစား ဖြစ်သည်။ ဖြစ်နိုင်ခြေ လုပ်ဆောင်ချက်သည် ကိန်းရှင်သည် အချို့သော တန်ဖိုးတစ်ခုပေါ်တွင် သက်ရောက်နိုင်ခြေကို ညွှန်ပြပြီး ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက်သည် ကိန်းရှင်၏ တိုးပွားလာနိုင်သည့် ဖြစ်နိုင်ခြေကို ဖော်ပြနေချိန်တွင် ဖြစ်သည်။

ထို့ကြောင့်၊ ဖြန့်ဖြူးမှု လုပ်ဆောင်ချက်ကို ဖြစ်နိုင်ခြေ လုပ်ဆောင်ချက်မှ တွက်ချက်သည်။

ဥပမာအနေဖြင့်၊ အထက်ဖော်ပြပါ လေ့ကျင့်ခန်းတွင် တွေ့ရနိုင်ခြေရှိသည့် လုပ်ဆောင်ချက်အပေါ် အခြေခံ၍ အကြွေစေ့လေးကြိမ်မှ ခေါင်းများရယူရန် ဖြန့်ဝေမှုလုပ်ဆောင်ချက်ကို တွက်ချက်ကြည့်ရှုနိုင်ပါသည်။

➤- ဖြန့်ဖြူးမှုလုပ်ဆောင်ချက် နမူနာကို ကြည့်ပါ ။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။