ယုံကြည်မှုကြားကာလခြားနားချက်ကို ဆိုလိုသည်။
အဓိပ္ပါယ်များကြားခြားနားချက်အတွက် ယုံကြည်မှုကြားကာလ (CI) ဆိုသည်မှာ လူဦးရေနှစ်ခုကြားတွင် စစ်မှန်သောခြားနားချက်ပါဝင်နိုင်ဖွယ်ရှိသော တန်ဖိုးများတစ်ခုဖြစ်ပြီး အချို့သောယုံကြည်မှုအဆင့်ကို ဆိုလိုပါသည်။
ဤသင်ခန်းစာတွင် အောက်ပါတို့ကို ရှင်းပြထားသည်။
- ဤယုံကြည်မှုကြားကာလကို ဖန်တီးရန် စေ့ဆော်မှု။
- ဤယုံကြည်မှုကြားကာလကို ဖန်တီးရန် ဖော်မြူလာ။
- ဤယုံကြည်မှုကြားကာလကို တွက်ချက်ပုံဥပမာ။
- ဒီယုံကြည်မှုကြားကာလကို ဘယ်လိုအဓိပ္ပာယ်ဖွင့်မလဲ။
CI ဆိုသည်မှာ စေ့ဆော်မှုကြား ခြားနားချက်
သုတေသီများသည် လူဦးရေနှစ်ခု၏ ကွာခြားချက်ကို ခန့်မှန်းလိုကြသည်။ ဤကွာခြားချက်ကို ခန့်မှန်းရန်၊ ၎င်းတို့သည် လူဦးရေတစ်ခုစီမှ ကျပန်းနမူနာတစ်ခုကို ကောက်ယူပြီး နမူနာတစ်ခုစီအတွက် ပျမ်းမျှအား တွက်ချက်မည်ဖြစ်သည်။ ထို့နောက် ၎င်းတို့သည် ပျမ်းမျှနှစ်ခုကြား ခြားနားချက်ကို နှိုင်းယှဉ်နိုင်သည်။
သို့သော် နမူနာဆိုလိုသည်များကြားက ခြားနားချက်သည် လူဦးရေဆိုလိုသည်များကြား စစ်မှန်သောကွာခြားချက်နှင့် ကိုက်ညီမှုရှိမရှိ အတိအကျမသိနိုင်ပေ။ ထို့ကြောင့် ၎င်းတို့နှစ်ဦးကြား ခြားနားမှုအတွက် ယုံကြည်မှုကြားကာလကို ဖန်တီးနိုင်သောကြောင့် ဖြစ်သည်။ ဤသည်မှာ ပံ့ပိုးပေးမည့် တန်ဖိုးများကြားတွင် စစ်မှန်သော ခြားနားချက် ပါဝင်နိုင်ဖွယ်ရှိသော လူဦးရေကို ဆိုလိုသည်။
ဥပမာအားဖြင့်၊ မတူညီသောလိပ်မျိုးစိတ်နှစ်ခုကြားရှိ ပျမ်းမျှအလေးချိန်ကွာခြားချက်ကို ခန့်မှန်းလိုသည်ဆိုပါစို့။ လူဦးရေတစ်ထောင်စီတွင် လိပ်ကောင်ရေ ထောင်ချီရှိသောကြောင့် လိပ်တစ်ကောင်ချင်းစီအလိုက် လှည့်ပတ်ပြီးချိန်တွယ်ရန် အချိန်ကုန်ပြီး စျေးကြီးသည်။
ယင်းအစား၊ လူဦးရေတစ်ခုစီမှ လိပ် 15 ကောင်၏ ရိုးရှင်းသောကျပန်းနမူနာကို ယူကာ နမူနာတစ်ခုစီ၏ ပျမ်းမျှအလေးချိန်ကို အသုံးပြု၍ လူဦးရေနှစ်ခုကြားရှိ ပျမ်းမျှအလေးချိန်၏ စစ်မှန်သောကွာခြားချက်ကို ခန့်မှန်းရန်-
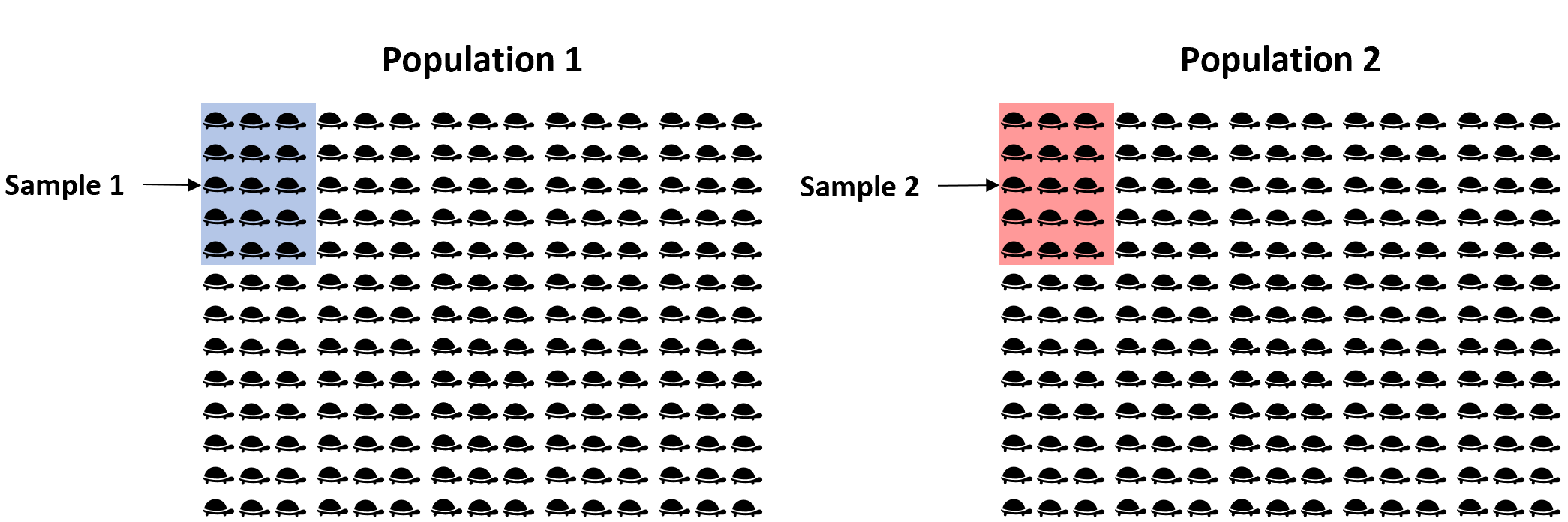
ပြဿနာမှာ ကျွန်ုပ်တို့၏နမူနာများသည် ကျပန်းဖြစ်သောကြောင့်၊ နမူနာနှစ်ခုကြားရှိ ပျမ်းမျှအလေးချိန်ကွာခြားချက်သည် လူဦးရေနှစ်ခုကြားရှိ ပျမ်းမျှအလေးချိန်ကွာခြားချက်နှင့် အတိအကျကိုက်ညီကြောင်း အာမခံချက်မရှိပါ။ ထို့ကြောင့် ဤမသေချာမရေရာမှုကို ဖမ်းယူရန်၊ လူဦးရေနှစ်ခုကြားရှိ ပျမ်းမျှအလေးချိန်၏ စစ်မှန်သောကွာခြားချက်ပါ၀င်နိုင်ဖွယ်ရှိသော တန်ဖိုးများစွာပါရှိသော ယုံကြည်မှုကြားကာလတစ်ခုကို ကျွန်ုပ်တို့ ဖန်တီးနိုင်သည်။
CI ဆိုသည်မှာ ခြားနားချက်အတွက် ဖော်မြူလာ
နည်းလမ်းနှစ်ခုကြား ခြားနားချက်အတွက် ယုံကြည်မှုကြားကာလကို တွက်ချက်ရန် အောက်ပါဖော်မြူလာကို ကျွန်ုပ်တို့ အသုံးပြုသည်-
ယုံကြည်မှုကြားကာလ = ( x 1 – x 2 ) +/- t*√((s p 2 /n 1 ) + (s p 2 /n 2 ))
ရွှေ-
- x 1 ၊ x 2 : နမူနာ 1 ၏ ဆိုလိုချက် ၊ နမူနာ 2 ၏ ဆိုလိုချက်
- t- ယုံကြည်မှုအဆင့်နှင့် လွတ်လပ်မှု (n 1 + n 2 -2) ဒီဂရီပေါ်မူတည်၍ t-အရေးပါသောတန်ဖိုး၊
- s p 2 : စုပေါင်းကွဲလွဲမှု
- n 1 ၊ n 2 : နမူနာအရွယ်အစား 1၊ နမူနာအရွယ်အစား 2
ရွှေ-
- စုပေါင်းကွဲလွဲမှုကို အောက်ပါအတိုင်း တွက်ချက်သည်- s p 2 = ((n 1 -1)s 1 2 + (n 2 -1)s 2 2 ) / (n 1 +n 2 -2)
- t-အရေးပါသောတန်ဖိုး t ကို ပြောင်းပြန် t ဖြန့်ဖြူးရေးဂဏန်းတွက်စက်ကို အသုံးပြု၍ တွေ့ရှိနိုင်သည်။
CI ဆိုသည်မှာ ခြားနားချက်အတွက် ဥပမာ
မတူညီသောလိပ်မျိုးစိတ်နှစ်ခုကြားရှိ ပျမ်းမျှအလေးချိန်ကွာခြားချက်ကို ခန့်မှန်းလိုသည်ဆိုပါစို့။ ထို့ကြောင့် လူဦးရေတစ်ခုစီမှ လိပ် ၁၅ ကောင်၏ ကျပန်းနမူနာကို ကျွန်ုပ်တို့ စုဆောင်းပါမည်။ ဤသည်မှာ နမူနာတစ်ခုစီအတွက် အကျဉ်းချုပ်ဒေတာဖြစ်သည်-
နမူနာ 1-
- x1 = 310
- s 1 = 18.5
- n 1 = 15
နမူနာ 2-
- x2 = 300
- s2 = 16.4
- n2 =15
ဤသည်မှာ လူဦးရေ၏ ပျမ်းမျှအလေးများ ကွာခြားချက်အတွက် မတူညီသော ယုံကြည်မှုကြားကာလများကို မည်သို့ရှာဖွေရမည်နည်း။
90% ယုံကြည်မှုကြားကာလ-
(310-300) +/- 1.70*√((305.61/15) + (305.61/15)) = [-0.8589၊ 20.8589]
95% ယုံကြည်မှုကြားကာလ-
(310-300) +/- 2.05*√((305.61/15) + (305.61/15)) = [-3.0757၊ 23.0757]
99% ယုံကြည်မှုကြားကာလ-
(310-300) +/- 2.76*√((305.61/15) + (305.61/15)) = [-7.6389၊ 27.6389]
မှတ်ချက်- Means Calculator အကြားကွာခြားမှုအတွက် Statistical Confidence Interval ကို အသုံးပြု၍ ဤယုံကြည်မှုကြားကာလကိုလည်း သင်ရှာဖွေနိုင်သည်။
ယုံကြည်မှုအဆင့်မြင့်လေ၊ ယုံကြည်မှုကြားကာလ ကျယ်လေလေဖြစ်ကြောင်း သတိပြုမိပါလိမ့်မည်။ ကျယ်ပြန့်သောကြားကာလများသည် စစ်မှန်သောလူဦးရေဆိုလိုရင်းပါ၀င်နိုင်ခြေပိုများသောကြောင့်၊ ဤကြားကာလသည် စစ်မှန်သောလူဦးရေဆိုလိုရင်းပါရှိသည်ကို ကျွန်ုပ်တို့ ပို၍ “ ယုံကြည်မှု” ရှိသင့်ပါသည်။
CI ဆိုသည်မှာ အဓိပ္ပာယ်ဖွ င့်ဆိုချက် ခြားနားချက်
ယုံကြည်မှုကြားကာလကို ကျွန်ုပ်တို့ အဓိပ္ပာယ်ဖွင့်ဆိုပုံမှာ-
[-3.0757၊ 23.0757] ၏ယုံကြည်မှုကြားကာလသည် လိပ်နှစ်ကောင်ကြားရှိ ပျမ်းမျှအလေးချိန်၏ စစ်မှန်သောကွာခြားချက်ပါ၀င်သည်ဟူသော အခွင့်အလမ်း 95% ရှိပါသည်။
ဤကြားကာလတွင် တန်ဖိုး “ 0” ပါ၀င်သောကြောင့် ဆိုလိုသည်မှာ ဤလူဦးရေနှစ်ခုမှ လိပ်များကြား ပျမ်းမျှအလေးချိန်မှာ ကွာခြားမှုမရှိဟု ဆိုလိုသည်။ တစ်နည်းဆိုရသော် ဤလူဦးရေနှစ်ခုမှ လိပ်များကြားတွင် ပျမ်းမျှအလေးချိန်ကွာခြားမှုရှိကြောင်း 95% ယုံကြည်မှုဖြင့် ကျွန်ုပ်တို့ မပြောနိုင်ပါ။