F distribution ကို အသုံးပြု၍ confidence interval တစ်ခုဖန်တီးနည်း

လူဦးရေ နှစ်ခု၏ ကွဲလွဲမှု ညီမျှခြင်း ရှိ၊ မရှိ ဆုံးဖြတ်ရန် ၊ σ ² ₁ / σ ² ₂ ကွဲလွဲမှု အချိုးကို တွက်ချက်နိုင်သည်၊ σ ² ₁ သည် လူဦးရေ 1 နှင့် σ ² ₂ သည် လူဦးရေ ကွဲလွဲမှု 2 ဖြစ်သည် ။

လူဦးရေကွဲလွဲမှုအချိုးအမှန်ကို ခန့်မှန်းရန်၊ ကျွန်ုပ်တို့သည် ယေဘူယျအားဖြင့် လူဦးရေတစ်ခုစီမှ ရိုးရှင်းသောကျပန်းနမူနာကို ယူပြီး နမူနာကွဲလွဲမှုအချိုး၊ s ₁ ² / s ₂ ² ၊ s ₁ ² နှင့် s ₂ ² တို့သည် နမူနာ 1 နှင့် နမူနာများအတွက် နမူနာကွဲလွဲမှုများဖြစ်သည် . 2 အသီးသီး။

ဤစမ်းသပ်မှုတွင် s ₁ ² နှင့် s ₂ ^{2 ကို} အရွယ်အစား n ₁ နှင့် n ₂ ၏ သီးခြားနမူနာများမှ တွက်ချက်သည်ဟု ယူဆသည်၊ နှစ်ခုစလုံးသည် ပုံမှန်ဖြန့်ဝေထားသော လူဦးရေမှဖြစ်သည်။

နောက်ထပ် ဤအချိုးသည် တစ်ခုမှဖြစ်သည်၊ လူဦးရေအတွင်း မညီမျှသောကွဲလွဲမှုများ၏ အထောက်အထားများ အားကောင်းလေဖြစ်သည်။

σ ² ₁ / σ ² ₂ အတွက် (1-α) 100% ယုံကြည်မှုကြားကာလကို အောက်ပါအတိုင်း သတ်မှတ်သည်။

(s ₁ ² / s ₂ ² ) * F _{n 1 -1, n 2 -1, α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n 2 -1, n 1 -1၊ α/2}

F _{n 2 -1၊ n 1 -1၊ α/2} နှင့် F _{n 1 -1၊ n 2 -1၊ α/2}   ရွေးချယ်ထားသော α အဆင့်အတွက် ဖြန့်ဖြူးမှု F ၏ အရေးကြီးသောတန်ဖိုးများဖြစ်သည်။

အောက်ပါဥပမာများသည် σ ² ₁ / σ ² ₂ အတွက် မတူညီသောနည်းလမ်းသုံးမျိုးဖြင့် ယုံကြည်မှုကြားကာလကို ဖန်တီးနည်းကို သရုပ်ဖော်သည်။

• လက်ဖြင့်
• Microsoft Excel ကိုသုံးပါ။
• R စာရင်းအင်းဆော့ဖ်ဝဲကိုအသုံးပြုခြင်း။

အောက်ပါဥပမာတစ်ခုစီအတွက်၊ ကျွန်ုပ်တို့သည် အောက်ပါအချက်အလက်များကို အသုံးပြုပါမည်။

• α = 0.05
• n ₁ = 16
• _n2 = ၁၁
• s ₁ ² = 28.2
• s ₂ ² = 19.3

ယုံကြည်မှုကြားကာလကို ကိုယ်တိုင်ဖန်တီးပါ။

σ ² ₁ / σ ² ₂ အတွက် ယုံကြည်မှုကြားကာလကို ကိုယ်တိုင်တွက်ချက်ရန်၊ ကျွန်ုပ်တို့တွင်ရှိသော နံပါတ်များကို ယုံကြည်မှုကြားကာလ ဖော်မြူလာတွင် ရိုးရိုးရှင်းရှင်း ထည့်သွင်းပါမည်-

(s ₁ ² / s ₂ ² ) * F _{n1-1, n2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n2-1, n1-1၊ α/2}

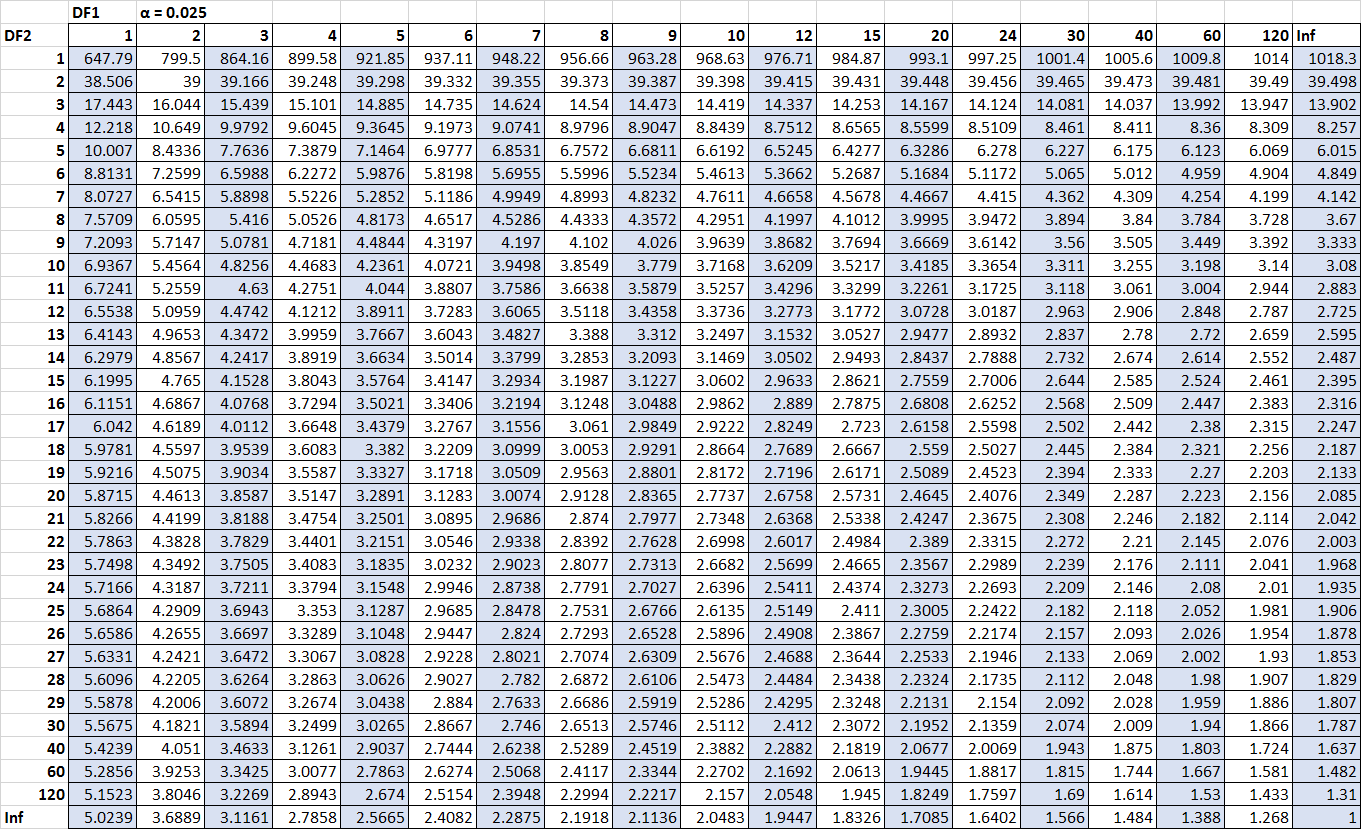
ကျွန်ုပ်တို့ ပျောက်နေသော တစ်ခုတည်းသော ကိန်းဂဏန်းများသည် အရေးကြီးသော တန်ဖိုးများဖြစ်သည်။ ကံကောင်းထောက်မစွာ၊ ကျွန်ုပ်တို့သည် ဖြန့်ဖြူးမှုဇယား F တွင် ဤအရေးကြီးသောတန်ဖိုးများကို ရှာဖွေတွေ့ရှိနိုင်သည် ။

F _{n2-1၊ n1-1၊ α/2} = F _{10၊ 15၊ 0.025} = 3.0602

F _{n1-1၊ n2-1၊ α/2} = 1/ F _{15၊ 10၊ 0.025} = 1/3.5217 = 0.2839၊

(ဇယားကို ချဲ့ကြည့်ရန် နှိပ်ပါ)

ယခု ကျွန်ုပ်တို့သည် နံပါတ်အားလုံးကို ယုံကြည်စိတ်ချမှုဖော်မြူလာကြားကာလတွင် ထည့်သွင်းနိုင်ပါပြီ-

(s ₁ ² / s ₂ ² ) * F _{n1-1, n2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n2-1, n1-1၊ α/2}

(28.2/19.3) * (0.2839) ≤ σ ² ₁ / σ ² ₂ ≤ (28.2/19.3) * (3.0602)၊

0.4148 ≤ σ ² ₁ / σ ² ₂ ≤ 4.4714၊

ထို့ကြောင့် လူဦးရေကွဲပြားမှုအချိုးအတွက် 95% ယုံကြည်မှုကြားကာလသည် (0.4148၊ 4.4714) ဖြစ်သည်။

Excel ကို အသုံးပြု၍ Confidence Interval ဖန်တီးခြင်း။

အောက်ဖော်ပြပါပုံသည် Excel ရှိ လူဦးရေကွဲပြားမှုအချိုးအတွက် 95% ယုံကြည်မှုကြားကာလကို တွက်ချက်နည်းကို ပြသထားသည်။ ယုံကြည်မှုကြားကာလ၏ အောက်နှင့်အထက် ကန့်သတ်ချက်များကို ကော်လံ E တွင် ပြသထားပြီး အောက်နှင့် အထက်ကန့်သတ်ချက်များကို ရှာဖွေရန် အသုံးပြုသည့် ဖော်မြူလာကို ကော်လံ F တွင် ပြသထားသည်-

ထို့ကြောင့် လူဦးရေကွဲပြားမှုအချိုးအတွက် 95% ယုံကြည်မှုကြားကာလသည် (0.4148၊ 4.4714) ဖြစ်သည်။ ယုံကြည်မှုကြားကာလကို ကိုယ်တိုင်တွက်ချက်သောအခါ ၎င်းသည် ကျွန်ုပ်တို့ရရှိသည့်အရာနှင့် ကိုက်ညီပါသည်။

R ကိုအသုံးပြု၍ ယုံကြည်မှုကြားကာလတစ်ခုဖန်တီးခြင်း။

အောက်ပါကုဒ်သည် R တွင် လူဦးရေကွဲပြားမှုအချိုးအတွက် 95% ယုံကြည်မှုကြားကာလကို တွက်ချက်နည်းကို ဖော်ပြသည်-

 #define significance level, sample sizes, and sample variances
alpha <- .05
n1 <- 16
n2 <- 11
var1 <- 28.2
var2 <- 19.3

#define F critical values
upper_crit <- 1/qf(alpha/2, n1-1, n2-1)
lower_crit <- qf(alpha/2, n2-1, n1-1)

#find confidence interval
lower_bound <- (var1/var2) * lower_crit
upper_bound <- (var1/var2) * upper_crit

#output confidence interval
paste0("(", lower_bound, ", ", upper_bound, " )")

#[1] "(0.414899337980266, 4.47137571035219 )"

ထို့ကြောင့် လူဦးရေကွဲပြားမှုအချိုးအတွက် 95% ယုံကြည်မှုကြားကာလသည် (0.4148၊ 4.4714) ဖြစ်သည်။ ယုံကြည်မှုကြားကာလကို ကိုယ်တိုင်တွက်ချက်သောအခါ ၎င်းသည် ကျွန်ုပ်တို့ရရှိသည့်အရာနှင့် ကိုက်ညီပါသည်။

ထပ်လောင်းအရင်းအမြစ်များ

F ဖြန့်ချီရေးဘုတ်ကို ဘယ်လိုဖတ်မလဲ။
Excel တွင် အရေးပါသော တန်ဖိုး F ကို မည်သို့ရှာမည်နည်း။