ရိုးရှင်းသော ကြမ်ဖက်မှု
ဤဆောင်းပါးတွင် ရိုးရှင်းသောကျပန်းနမူနာသည် အဘယ်နည်းနှင့် ရိုးရှင်းသောကျပန်းနမူနာအမျိုးအစားများ ရှိသည်ကို သင်လေ့လာပါမည်။ ထို့အပြင်၊ ကျွန်ုပ်တို့သည် ဥပမာတစ်ခုအားဖြင့် ရိုးရှင်းသောကျပန်းနမူနာကို မည်သို့လုပ်ဆောင်ကြောင်း ရှင်းပြထားသည်။ နောက်ဆုံးတွင်၊ ရိုးရိုးကျပန်းနမူနာယူခြင်း၏ အားသာချက်များနှင့် အားနည်းချက်များကို သင်မြင်နိုင်မည်ဖြစ်သည်။
ရိုးရှင်းသောကျပန်းနမူနာကဘာလဲ။
ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ ရိုးရှင်းသောကျပန်းနမူနာ သည် လေ့လာမှုတစ်ခုအတွက်နမူနာကိုရွေးချယ်ရန်အသုံးပြုသော ဖြစ်နိုင်ခြေရှိသောနည်းလမ်းတစ်ခုဖြစ်သည်။ ရိုးရှင်းသောကျပန်းနမူနာကောက်ယူခြင်း၏ အဓိကလက္ခဏာမှာ ကိန်းဂဏန်းစာရင်းအင်းလူဦးရေ၏ဒြပ်စင်တစ်ခုစီကို လေ့လာထားသောနမူနာတွင်ပါဝင်နိုင်ခြေတူညီသောဖြစ်နိုင်ခြေကိုပေးဆောင်ခြင်းဖြစ်သည်။
ရိုးရှင်းသောကျပန်းနမူနာတွင်၊ နမူနာဒြပ်စင်များကို ကျပန်းရွေးချယ်ထားသောကြောင့် ထွက်ပေါ်လာသောနမူနာသည် လုံးဝကျပန်းဖြစ်သည်။
ထို့ကြောင့်၊ ရိုးရှင်းသောကျပန်းနမူနာကိုအသုံးပြု၍ ပေးထားသောနမူနာကိုရရှိရန်ဖြစ်နိုင်ခြေသည် အခြားနမူနာတစ်ခုခုရရှိရန်ဖြစ်နိုင်ခြေနှင့် ညီမျှသည်။ ဤဖြစ်နိုင်ခြေကို မည်ကဲ့သို့ တွက်ချက်ထားသည်ကို အောက်တွင် ကြည့်ရှုပါမည်။
နမူနာတစ်ခုမှ တစ်ဦးချင်းစီကို ရွေးချယ်ရန် အခြားနည်းလမ်းများ ရှိသည်ကို သတိရပါ။ အသုံးအများဆုံးနမူနာအမျိုးအစားများမှာ အဓိကအားဖြင့်-
- ရိုးရှင်းသော ကြမ်ဖက်မှု
- အချိုးကျနမူနာ
- စနစ်တကျ နမူနာယူခြင်း။
- အစုအဖွဲ့နမူနာ
ရိုးရှင်းသော ကျပန်းနမူနာ၏ သဘောတရားသည် နားလည်ရန် အလွယ်ကူဆုံး အမျိုးအစားဖြစ်သည်မှာ သေချာသည်၊ သို့သော် ၎င်းသည် တစ်ခါတစ်ရံတွင် ၎င်း၏ ကျပန်းသဘောသဘာဝကြောင့် အတိအကျ အကောင်အထည်ဖော်ရန် အရှုပ်ထွေးဆုံး ဖြစ်သွားသည်။
ရိုးရှင်းသောနမူနာယူနည်း
ရိုးရှင်းသောကျပန်းနမူနာလုပ်ဆောင်ရန် အဆင့်များမှာ အောက်ပါအတိုင်းဖြစ်သည် ။
- လူဦးရေ၏ အစိတ်အပိုင်းများအားလုံးကို စာရင်းပြုစုပါ။
- လူဦးရေရှိဒြပ်စင်တစ်ခုစီသို့ နံပါတ်စဉ် (1၊ 2၊ 3၊…၊ n) ကို သတ်မှတ်ပါ ။
- လိုချင်သော နမူနာအရွယ်အစားကို သတ်မှတ်ပါ။
- ရွေးချယ်ထားသောနမူနာအရွယ်အစားအတိုင်း နံပါတ်များစွာထုတ်ပေးရန် ကျပန်းနံပါတ်ဂျင်နရေတာကို သုံးပါ။
- ထုတ်ပေးထားသော နံပါတ်များအတွက် သတ်မှတ်ထားသော ပုဂ္ဂိုလ်များ သည် နမူနာ၏ အစိတ်အပိုင်းအဖြစ် ရွေးချယ်ခံရသူများဖြစ်သည်။
ကျပန်းနံပါတ်များထုတ်လုပ်ရန် နည်းလမ်းများစွာရှိပါသည်၊ သမားရိုးကျဆုံးသော ထီနည်းလမ်းနှင့် နံပါတ်ဇယားနည်းလမ်းများမှာ-
- ကံစမ်းမဲနည်းလမ်းတွင် ဂဏန်းများအားလုံးကို သေတ္တာတစ်ခုအတွင်းထည့်ကာ ၎င်းတို့ကို ရှပ်ထိုးကာ နံပါတ်များကို ကျပန်းဆွဲထုတ်ခြင်း ပါဝင်သည်။
- နံပါတ်ဇယားနည်းလမ်းတွင် ဖြစ်နိုင်သည့်နံပါတ်များပါရှိသော ဇယားတစ်ခုမှ နံပါတ်များကို ကျပန်းရွေးချယ်ခြင်း ပါဝင်သည်။
သင်သည် ယခင်နည်းလမ်းနှစ်ခုမှ တစ်ခုခုကို အသုံးပြုနိုင်သော်လည်း ၎င်းတို့သည် အချိန်ပိုလိုအပ်ပြီး သေးငယ်သောနမူနာအရွယ်အစားများအတွက် ပိုသင့်လျော်ပါသည်။ လက်ရှိတွင်၊ ကွန်ပြူတာပရိုဂရမ်များကို ကျပန်းနံပါတ်များပိုမိုမြန်ဆန်စွာထုတ်ပေးရန်အသုံးပြုသည်၊ ဥပမာအားဖြင့် သင်သည် Excel ပရိုဂရမ်ကို အသုံးပြုနိုင်သည်။
အခြားတစ်ဖက်တွင်၊ ဖြစ်နိုင်ခြေအနည်းဆုံးနမူနာအမှားရှိစေရန်အတွက် နမူနာအရွယ်အစားသည် လုံလောက်မှုရှိရမည်ကို ထည့်သွင်းစဉ်းစားရပါမည်။ စံပြနမူနာအရွယ်အစားကို ရှာဖွေခြင်းသည် အသေးအဖွဲမဟုတ်ပါ။ ၎င်းနှင့်ပတ်သက်ပြီး သံသယများရှိပါက ကျွန်ုပ်တို့၏ဝဘ်ဆိုဒ်တွင် ၎င်းကိုပြုလုပ်နည်းကို ရှင်းပြထားသည့် ဆောင်းပါးအတွက် သင်ရှာဖွေနိုင်ပါသည်။
ရိုးရှင်းသော ကျပန်းနမူနာ နမူနာ
ရိုးရှင်းသော ကျပန်းနမူနာ၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို ကျွန်ုပ်တို့မြင်သည်နှင့်၊ ဤနမူနာပုံစံကို မည်သို့လုပ်ဆောင်ကြောင်း ဖြေရှင်းနိုင်သော ဥပမာတစ်ခုကို ကျွန်ုပ်တို့တွေ့ရပါမည်။
ဥပမာအားဖြင့်၊ ကုမ္ပဏီတစ်ခုတွင် အလုပ်သမား 2000 ရှိပြီး ကျွန်ုပ်တို့သည် နမူနာနမူနာ 400 ဖြင့် ကိန်းဂဏန်းလေ့လာမှုကို လုပ်ဆောင်လိုပါက နမူနာ၏တစ်စိတ်တစ်ပိုင်းဖြစ်မည့်သူများကို ရွေးချယ်ရန်အတွက် ရိုးရှင်းသောကျပန်းနမူနာဖြင့် ပထမဆုံးလုပ်ဆောင်ရမည့်အရာ ပါဝင်ပါသည်။ ဝန်ထမ်းတစ်ဦးစီကို နံပါတ် ၁ မှ ၂၀၀၀ အထိ သတ်မှတ်ပေးသည်။
နံပါတ်များသတ်မှတ်ပြီးနောက်၊ ကျွန်ုပ်တို့သည် ကျပန်းနံပါတ် 400 ကိုရွေးချယ်ရန်လိုအပ်သည်။ ဤကိစ္စတွင်၊ နမူနာအရွယ်အစားသည် အလွန်ကြီးမားသောကြောင့် Excel ကဲ့သို့သော ကွန်ပျူတာဆော့ဖ်ဝဲကို အသုံးပြုခြင်းသည် အကောင်းဆုံးဖြစ်သည်။
ထို့နောက် လေ့လာမှုတွင် ပါဝင်ရန် ရွေးချယ်ထားသည့် အလုပ်သမား ၄၀၀ သည် ယခင်အဆင့်တွင် သတ်မှတ်ပေးထားသည့် အရေအတွက်ကို သတ်မှတ်ပေးမည့်သူများ ဖြစ်မည်ဖြစ်သည်။
ဤဥပမာတွင် ပစ္စည်း 400 သည် လုံလောက်သောကိုယ်စားပြုနမူနာအရွယ်အစားဟုယူဆခဲ့သော်လည်း ယုတ္တိနည်းအားဖြင့် ဤနံပါတ်သည် စမ်းသပ်မှုပေါ်မူတည်၍ ပြောင်းလဲသွားမည်ဖြစ်သည်။
Simple Random Sampling အမျိုးအစားများ
ရိုးရှင်းသော ကျပန်းနမူနာ နှစ်မျိုးရှိသည်။
- အစားထိုးခြင်းဖြင့် ရိုးရှင်းသော ကျပန်းနမူနာယူခြင်း – နမူနာဘောင်၏ ရွေးချယ်ထားသော ဒြပ်စင်ကို ပြန်သွားပြီး ထပ်မံရွေးချယ်နိုင်ပါသည်။
- အစားထိုးခြင်းမရှိဘဲ ရိုးရှင်းသောကျပန်းနမူနာယူခြင်း – နမူနာ၏တစ်စိတ်တစ်ပိုင်းဖြစ်ရန် ရွေးချယ်ထားသည့်အရာအား ဖျက်လိုက်ပြီး ရွေးချယ်၍မရတော့ပါ။
အစားထိုးခြင်းနှင့်အတူ ရိုးရှင်းသောကျပန်းနမူနာသည် အရိုးရှင်းဆုံးနမူနာအမျိုးအစားဖြစ်သည်၊ အဘယ်ကြောင့်ဆိုသော် နမူနာမှအရာတစ်ခုကိုရွေးချယ်ရန် တူညီသောလုပ်ငန်းစဉ်ကို အမြဲထပ်ခါထပ်ခါပြုလုပ်သောကြောင့်ဖြစ်သည်။ သို့သော်၊ အစားထိုးခြင်းမရှိဘဲ ရိုးရှင်းသောကျပန်းနမူနာကို ပိုမိုတိကျသောကြောင့် ပိုမိုတွင်ကျယ်စွာအသုံးပြုပါသည်။ အမျိုးအစားနှစ်မျိုးလုံးကို အောက်တွင် အသေးစိတ်ရှင်းပြထားပါသည်။
အစားထိုးခြင်းနှင့် ရိုးရှင်းသော ကျပန်းနမူနာ
အစားထိုးခြင်းနှင့် ရိုးရှင်းသော ကျပန်းနမူနာယူခြင်းတွင် ရွေးချယ်ထားသော အရာတစ်ခုစီကို နမူနာဘောင်သို့ ပြန်ပို့ခြင်းတွင် ၎င်းကို ထပ်မံရွေးချယ်ရန် ဖြစ်နိုင်ခြေရှိစေရန် ပါဝင်သည်။
ထို့ကြောင့်၊ ဤအရာသည် အလွန်မဖြစ်နိုင်သော်လည်း အကြိမ်များစွာ ရွေးချယ်ထားသော အရာတစ်ခုနှင့် နမူနာတစ်ခုကို ရယူရန် ဖြစ်နိုင်သည်။
သင်္ချာနည်းအရ၊ ထုတ်ယူမှုတစ်ခုစီ၏ ဖြစ်နိုင်ခြေများသည် တူညီသောကြောင့် ဤသည်မှာ အလွန်ရိုးရှင်းသော နမူနာပုံစံတစ်ခုဖြစ်သည်။ ထို့ကြောင့် အခြားသူများရှေ့တွင် ဤနမူနာနည်းပညာကို စတင်လေ့လာခြင်းသည် သာမာန်ဖြစ်သည်။
အစားထိုးခြင်းနှင့် ရိုးရှင်းသောကျပန်းနမူနာများတွင်၊ အချို့သောအမှာစာဖြင့် နမူနာရယူခြင်း၏ဖြစ်နိုင်ခြေကို အောက်ပါဖော်မြူလာကို အသုံးပြု၍ တွက်ချက်နိုင်သည်-
![]()
ဖြစ်ပါစေ။
![]()
လူဦးရေ စုစုပေါင်း၏ ဒြပ်စင်အရေအတွက်နှင့်
![]()
လုပ်ဆောင်မည့် အမှီအခိုကင်းသော ထုတ်ယူမှုအရေအတွက်။
အခြားတစ်ဖက်တွင်၊ အမိန့်သည် အရေးမကြီးသောအခါ၊ နမူနာတစ်ခုရရှိရန် ဖြစ်နိုင်ခြေကို အောက်ပါအသုံးအနှုန်းဖြင့် တွက်ချက်သည်-
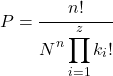
ရွှေ
![]()
လွတ်လပ်သော ထုတ်ယူမှုအရေအတွက်၊
![]()
နမူနာနှင့် မတူညီသော ဒြပ်စင်အရေအတွက်
![]()
ပစ္စည်းကို ဘယ်နှစ်ခါ ပေါ်လာစေချင်လဲ။
![]()
နမူနာတွင်။
နောက်ဆုံးတွင်၊ ဒြပ်စင်၏ပါဝင်နိုင်ခြေကိုရှာဖွေရန်
![]()
ဆိုလိုသည်မှာ ဒြပ်စင်ပါဝင်ခြင်း၏ ဖြစ်နိုင်ခြေကိုဆိုလိုသည်။
![]()
ဥပမာတွင်၊ အောက်ပါပုံသေနည်းကို အသုံးပြုသင့်သည်-
![]()
အစားထိုးခြင်းမရှိဘဲ ရိုးရှင်းသောကျပန်းနမူနာ
အစားထိုးခြင်းမပြုဘဲ ရိုးရှင်းသောကျပန်းနမူနာများတွင် လိုချင်သောနမူနာအရွယ်အစားညွှန်ပြသည့်အတိုင်း လူများစွာထဲမှ နမူနာတစ်ခုကို ရွေးချယ်ခြင်းတွင် ပါဝင်ပြီး တစ်ခုချင်းစီကို ထပ်မံရွေးချယ်၍မရတော့ပါ။ ထို့ကြောင့်၊ ရွေးချယ်ထားသော အရာတစ်ခုစီကို ဖျက်ပြီး အစားထိုးမည်မဟုတ်ပါ။
ကျွန်ုပ်တို့သည် ရိုးရှင်းသောကျပန်းနမူနာအကြောင်းပြောသောအခါ၊ ၎င်းသည် လက်တွေ့တွင်အသုံးအများဆုံးဖြစ်သောကြောင့် လူတစ်ဦးချင်းစီကို အစားမထိုးနိုင်သော အရာများကို ပုံမှန်အားဖြင့် ရည်ညွှန်းပါသည်။
အစားထိုးခြင်းနှင့်အတူ ရိုးရှင်းသောကျပန်းနမူနာဖြင့် အချို့သောအမှာစာဖြင့်နမူနာရယူခြင်း၏ဖြစ်နိုင်ခြေကိုဆုံးဖြတ်ရန်၊ အောက်ပါဖော်မြူလာကိုအသုံးပြုသည်-
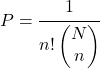
ဖြစ်ပါစေ။
![]()
လူဦးရေနှင့် စုစုပေါင်းဒြပ်စင်အရေအတွက်
![]()
လုပ်ဆောင်ရန် မှီခိုထုတ်ယူမှု အရေအတွက်။
အခြားတစ်ဖက်တွင်၊ ထုတ်ယူမှုအမိန့်ကို ထည့်သွင်းစဉ်းစားခြင်းမပြုပါက၊ နမူနာတစ်ခုရရှိရန် ဖြစ်နိုင်ခြေမှာ-
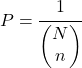
နောက်ဆုံးတွင်၊ အစားထိုးခြင်းမရှိဘဲ ရိုးရှင်းသောကျပန်းနမူနာတွင် ဒြပ်စင်တစ်ခုပါဝင်နိုင်ခြေကို Laplace ၏စည်းမျဉ်းကိုအသုံးပြုခြင်းဖြင့် တွက်ချက်သည်-
![]()
Simple Random Sampling ၏ အားသာချက်များနှင့် အားနည်းချက်များ
ရိုးရှင်းသော ကျပန်းနမူနာတွင် အောက်ပါ အားသာချက်များနှင့် အားနည်းချက်များ ရှိသည်။
| အားသာချက် | အားနည်းချက်များ |
|---|---|
| နားလည်ဖို့လွယ်တယ်။ | လူဦးရေ၏ အစိတ်အပိုင်းအားလုံး၏ စာရင်းတစ်ခု လိုအပ်ပါသည်။ |
| ဖြစ်နိုင်သည့်နမူနာများအားလုံးသည် တူညီပါသည်။ | ကြီးမားသောနမူနာအရွယ်အစားများဖြင့် ၎င်းသည် အလွန်စျေးကြီးနိုင်ပါသည်။ |
| ကိုယ်စားပြုနမူနာများကို အများအားဖြင့် ရယူကြသည်။ | ၎င်းတွင် ပိုကြီးသောနမူနာအမှားများ ရှိတတ်သည်။ |
| နမူနာယူရန် နည်းပညာဗဟုသုတ မလိုအပ်ပါ။ | လေ့လာခဲ့သော နယ်ပယ်တွင် သုတေသီရှိနိုင်သည့် အသိပညာကို အသုံးချ၍မရပါ။ |
| ပျမ်းမျှနှင့် သွေဖည်မှုများကို လျင်မြန်စွာ တွက်ချက်နိုင်စေပါသည်။ | နမူနာသည် အလွန်သေးငယ်ပါက ကိုယ်စားမပြုနိုင်ပါ။ |
| ဒေတာခွဲခြမ်းစိတ်ဖြာရန် statistical software ရှိပါသည်။ | တစ်ဦးချင်းအင်တာဗျူးများလိုအပ်သော လေ့လာမှုများအတွက် မသင့်လျော်ပါ။ |
ကျွန်ုပ်တို့တွေ့မြင်ခဲ့ရသည့်အတိုင်း၊ ရိုးရှင်းသောကျပန်းနမူနာ၏အဓိကလက္ခဏာများထဲမှတစ်ခုမှာ နားလည်ရန်နှင့်ရှင်းပြရန်လွယ်ကူခြင်းပင်ဖြစ်သည်။ အမှန်မှာ၊ နမူနာကောက်ယူသူသည် ခွဲခြမ်းစိတ်ဖြာမှုနယ်ပယ်တွင် ကျွမ်းကျင်သူဖြစ်ရန် မလိုအပ်ပါ။ သို့ရာတွင်၊ ၎င်းသည် ခွန်အားနှင့် အားနည်းချက် နှစ်မျိုးလုံးဖြစ်သည်၊ အကြောင်းမှာ အခြားနမူနာပုံစံများတွင် ပိုမိုကောင်းမွန်သောနမူနာကိုရရှိရန် အကဲခတ်သူ၏အသိပညာကို အသုံးချနိုင်သောကြောင့်ဖြစ်သည်။
အလားတူပင်၊ နမူနာကောက်ယူခြင်းသည် ကျပန်းဖြစ်သောကြောင့်၊ လေ့လာထားသောနမူနာကို အခြားနမူနာပုံစံများနှင့်မတူဘဲ ဤသို့မဟုတ်ထိုဒြပ်စင်ကိုဖွဲ့စည်းရန် ဖြစ်နိုင်ခြေမှာ ညီမျှပါသည်။
လူဦးရေ၏ ကိုယ်စားလှယ်နမူနာများကို အများအားဖြင့် ရရှိသော်လည်း၊ ရိုးရှင်းသောကျပန်းနမူနာများတွင် နမူနာယူမှုအမှားသည် အခြားနမူနာအမျိုးအစားများနှင့် နှိုင်းယှဉ်ပါက ကြီးမားပါသည်။ ထို့အပြင် လူတစ်ဦးချင်းစီ၏ အရွယ်အစားသည် သေးငယ်ပါက နမူနာကိုပင် ကိုယ်စားပြုနိုင်မည်မဟုတ်ပေ။
ရိုးရှင်းသောကျပန်းနမူနာကောက်ယူခြင်း၏ အလွန်ဆွဲဆောင်မှုရှိသော ပိုင်ဆိုင်မှုတစ်ခုမှာ ကိန်းဂဏန်းတွက်ချက်မှုများကို လျင်မြန်စွာလုပ်ဆောင်နိုင်စေသည့် ကွန်ပျူတာပရိုဂရမ်များကို အသုံးပြု၍ လုပ်ဆောင်နိုင်ခြင်းဖြစ်သည်။
နောက်ဆုံးတွင်၊ ရိုးရှင်းသောကျပန်းနမူနာသည် အခြားနမူနာအမျိုးအစားများထက်၊ အထူးသဖြင့် ကျယ်ပြန့်စွာပြန့်ကျဲနေသောလူဦးရေများတွင် သုတေသနအတွက် အရင်းအမြစ်များပိုမိုအသုံးပြုရန်လိုအပ်နိုင်သောကြောင့် ရိုးရှင်းသောကျပန်းနမူနာကို သတိပြုသင့်သည်။ ဥပမာအားဖြင့်၊ ၎င်းသည် ကျပန်းနမူနာယူခြင်းဖြစ်သောကြောင့် လေ့လာမှုပြုလုပ်ရန် ရွေးချယ်ခံရသူများသည် ပထဝီဝင်အနေအထားအရ ကျယ်ပြန့်စွာ ပြန့်ကျဲနေနိုင်ပြီး ထို့ကြောင့် မျက်နှာချင်းဆိုင်တွေ့ဆုံမေးမြန်းမှုများ ပြုလုပ်ခြင်းသည် ပို၍စျေးကြီးမည်ဖြစ်သည်။