ရိုးရှင်းသော linear ဆုတ်ယုတ်မှု

အားဖြင့် Benjamin Anderson ဩဂုတ် 2, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးသည် ကိန်းဂဏန်းစာရင်းဇယားများတွင် ရိုးရှင်းသော မျဉ်းကြောင်းပြန်ဆုတ်ခြင်းအကြောင်းနှင့် ၎င်းကိုလုပ်ဆောင်ပုံတို့ကို ရှင်းပြထားသည်။ အလားတူ၊ ရိုးရှင်းသော linear regression calculator ကိုဖြေရှင်းပြီး ရိုးရှင်းသော linear regression calculator ကို အွန်လိုင်းတွင် သင်တွေ့လိမ့်မည်။

ရိုးရှင်းသော linear regression ဆိုတာ ဘာလဲ။

ရိုးရှင်းသော linear regression သည် အမှီအခိုကင်းသော ကိန်းရှင်တစ်ခုအား ဆက်စပ်ရန် အသုံးပြုသည့် ကိန်းဂဏန်းစံနမူနာတစ်ခုဖြစ်ပြီး ကိန်းရှင်နှစ်ခုကြားရှိ ဆက်စပ်မှုအား အနီးစပ်ဆုံး ခန့်မှန်းရန် ကြိုးစားပါသည်။

ထို့ကြောင့်၊ ရိုးရှင်းသော linear regression ကို variable နှစ်ခု linearly ဆက်စပ်နေသော equation ကိုရှာရန် အသုံးပြုပါသည်။ ယုတ္တိဗေဒအရ၊ ကိန်းရှင်နှစ်ခုကြားရှိ ဆက်နွယ်မှုသည် linear ဖြစ်ရမည်၊ မဟုတ်ပါက အခြား regression model အမျိုးအစားကို အသုံးပြုရပါမည်။

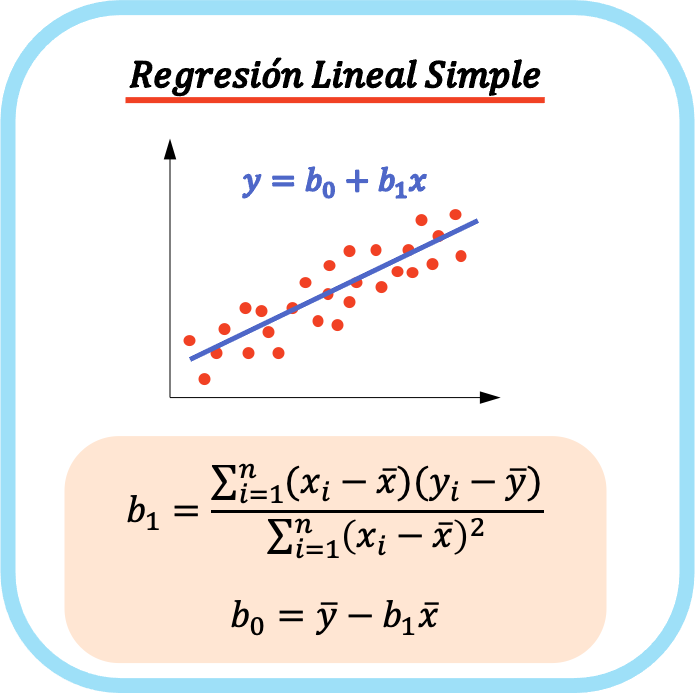
ရိုးရှင်းသော linear regression model ၏ ညီမျှခြင်းတွင် coefficients နှစ်ခုဖြင့် ဖွဲ့စည်းထားသည်- ညီမျှခြင်း (b ₀ ) နှင့် variable နှစ်ခုကြားရှိ ဆက်စပ်ကိန်း (b ₁ )။ ထို့ကြောင့်၊ ရိုးရိုးမျဉ်းကြောင်းဆုတ်ယုတ်မှုပုံစံအတွက် ညီမျှခြင်းမှာ y=b ₀ +b ₁ x ဖြစ်သည်။

$y=b_0+b_1x$

ရိုးရှင်းသော မျဉ်းကြောင်းဆုတ်ယုတ်မှုတစ်ခုအတွက် ညီမျှခြင်းအား မျဉ်းဖြောင့်အဖြစ် ပုံဆွဲထားသောကြောင့် ကိန်းဂဏန်း b ₀ သည် ကြားဖြတ်ဖြစ်ပြီး ဖော်ကိန်း b ₁ သည် မျဉ်း၏လျှောစောက်ဖြစ်သည်။

ရိုးရှင်းသော linear regression ဖော်မြူလာများ

ရိုးရှင်းသော linear regression ၏ coefficients များကို တွက်ချက်ရန် ဖော်မြူလာများမှာ အောက်ပါအတိုင်းဖြစ်သည် ။

👉 ဒေတာအစုံအတွက် ရိုးရှင်းသော linear regression ၏ coefficients များကို တွက်ချက်ရန် အောက်ပါ ဂဏန်းပေါင်းစက်ကို သင်အသုံးပြုနိုင်ပါသည်။

ရိုးရှင်းသော linear regression model မှ ထွက်ပေါ်လာသော ညီမျှခြင်းသည် လေ့လာတွေ့ရှိမှုအားလုံး၏ အတိအကျတန်ဖိုးကို ခန့်မှန်းနိုင်လိမ့်မည်မဟုတ်ပေ။ ထို့ကြောင့် ကျန်ရှိသောတန်ဖိုးကို linear regression model မှ ခန့်မှန်းထားသော တန်ဖိုးများကြား ခြားနားချက်အဖြစ် သတ်မှတ်သည်။

$e_i=y_i-\widehat{y}_i$

ရိုးရှင်းသော linear regression model ၏ ပန်းတိုင်သည် ကျန်ရှိသော လေးထောင့်များကို လျှော့ချရန်ဖြစ်သည်၊ ဆိုလိုသည်မှာ၊ ရိုးရှင်းသော linear regression သည် အနည်းဆုံး စတုရန်းဆိုင်ရာ စံသတ်မှတ်ချက်များအပေါ် အခြေခံထားခြင်းဖြစ်သည် ။

ရိုးရှင်းသော linear regression ၏ ကွန်ကရစ်ဥပမာ

ရိုးရှင်းသော linear regression method ကို နားလည်သဘောပေါက်ရန် အပြီးသတ်ရန်၊ ဤတွင်၊ ရိုးရှင်းသော linear regression model ၏ equation ကို statistical data set တစ်ခုမှ တွက်ချက်သည့် လက်တွေ့ကျသော အဆင့်ဆင့် ဥပမာတစ်ခုဖြစ်သည်။

စာရင်းအင်းစာမေးပွဲကိုဖြေဆိုပြီးနောက် ကျောင်းသားငါးဦးအား စာမေးပွဲအတွက် စာသင်ချိန်မည်မျှကြာအောင် သင်ကြားခဲ့ရကြောင်း မေးမြန်းခဲ့သည်။ အချက်အလက်များကို အောက်ပါဇယားတွင် ဖော်ပြထားပါသည်။ ရရှိလာသော အတန်းနှင့် အတန်းချိန်များကို မျဉ်းသားစွာ ဆက်စပ်နိုင်ရန် စုဆောင်းထားသော စာရင်းအင်းဒေတာ၏ ရိုးရှင်းသော မျဉ်းဖြောင့်ဆုတ်ယုတ်မှုပုံစံကို လုပ်ဆောင်ပါ။

ရိုးရှင်းသော linear regression model ကို အကောင်အထည်ဖော်ရန်အတွက် ညီမျှခြင်း၏ coefficients b ₀ နှင့် b ₁ ကို ဆုံးဖြတ်ရမည်ဖြစ်ပြီး၊ ယင်းအတွက်၊ အထက်ပိုင်းတွင် တွေ့ရသည့် ဖော်မြူလာများကို အသုံးပြုရပါမည်။

သို့သော်၊ ရိုးရှင်းသော မျဉ်းကြောင်းဆုတ်ယုတ်မှု ဖော်မြူလာများကို ကျင့်သုံးရန်၊ အမှီအခိုကင်းသော ကိန်းရှင်၏ ဆိုလိုချက်နှင့် မှီခိုကိန်းရှင်၏ ပျမ်းမျှအား တွက်ချက်ရပါမည်-

$\begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}$

ယခု ကျွန်ုပ်တို့သည် ကိန်းရှင်များ၏ အဓိပ္ပါယ်ကို သိရှိပြီး၊ ကျွန်ုပ်တို့သည် သက်ဆိုင်ရာ ဖော်မြူလာကို အသုံးပြု၍ မော်ဒယ်၏ ဖော်မြူကိန်း b ₁ ကို တွက်ချက်သည်-

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}$

နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် သက်ဆိုင်ရာ ဖော်မြူလာကို အသုံးပြု၍ မော်ဒယ်၏ ကိန်းဂဏန်း b ₀ ကို တွက်ချက်သည်-

$\begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}$

အတိုချုပ်အားဖြင့်၊ ပြဿနာ၏ရိုးရှင်းသော linear regression model အတွက် ညီမျှခြင်းမှာ-

$y=2,0294+0,4412x$

အောက်တွင် နမူနာဒေတာ၏ ဂရပ်ဖစ်ကိုယ်စားပြုမှုအပြင် ရိုးရှင်းသော linear regression model ၏ မျဉ်းဖြောင့်ကို သင်တွေ့မြင်နိုင်သည်-

နောက်ဆုံးတွင်၊ ရိုးရှင်းသော မျဉ်းဖြောင့်ဆုတ်ယုတ်မှုပုံစံ၏ ညီမျှခြင်းကို တွက်ချက်ပြီးသည်နှင့် ကျန်အရာအားလုံးသည် ရရှိသောရလဒ်ကို အနက်ဖွင့်ရန်ဖြစ်သည်။ ဤအတွက်၊ ဆုတ်ယုတ်မှုပုံစံ၏ အဆုံးအဖြတ်ပေးသည့်ကိန်းကို တွက်ချက်ရန် မရှိမဖြစ်လိုအပ်သည်၊ ကျွန်ုပ်တို့၏ ဝဘ်ဆိုက်ရှိ သက်ဆိုင်ရာ ဆောင်းပါးကို ရှာဖွေခြင်းဖြင့် ၎င်းကို မည်သို့လုပ်ဆောင်သည်ကို သင်တွေ့နိုင်ပါသည်။

ရိုးရှင်းသော Linear Regression ယူဆချက်များ

ရိုးရှင်းသော linear regression ကိုလုပ်ဆောင်ရန်အတွက် အောက်ပါယူဆချက်များကို ဖြည့်ဆည်းပေးရမည်-

လွတ်လပ်ရေး : တွေ့ရှိရသော အကြွင်းအကျန်များသည် တစ်ခုနှင့်တစ်ခု အမှီအခိုကင်းရမည်။ စံပြလွတ်လပ်မှုကို သေချာစေရန် ဘုံနည်းလမ်းမှာ နမူနာကောက်ယူခြင်းလုပ်ငန်းစဉ်တွင် ကျပန်းထည့်သွင်းခြင်းဖြစ်ပါသည်။
Homoscedasticity : အကြွင်းအကျန်များ၏ ကွဲလွဲမှုများတွင် တူညီမှုရှိရမည်၊ ဆိုလိုသည်မှာ အကြွင်းအကျန်များ၏ ကွဲလွဲမှုမှာ စဉ်ဆက်မပြတ်ရှိနေရမည်ဖြစ်သည်။
Normality : ကျန်ရှိသောပစ္စည်းများကို ပုံမှန်ဖြန့်ဝေရပါမည် သို့မဟုတ် တစ်နည်းအားဖြင့်ဆိုလိုရင်း 0 ဖြင့် ပုံမှန်ဖြန့်ဝေမှုအတိုင်း လုပ်ဆောင်ရမည်ဖြစ်သည်။
Linearity – အမှီအခိုကင်းသော ကိန်းရှင်နှင့် မှီခိုကိန်းရှင်ကြား ဆက်ဆံရေးသည် မျဉ်းဖြောင့်ဖြစ်သင့်သည်။

ရိုးရှင်းသော Linear Regression ဂဏန်းတွက်စက်

ကိန်းရှင်နှစ်ခုကြားရှိ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုပုံစံကို ကိုက်ညီစေရန် အောက်ဖော်ပြပါ ဂဏန်းတွက်စက်တွင် နမူနာဒေတာကို ချိတ်ပါ။ သင်သည် ဒေတာအတွဲများကို ခွဲခြားထားရန် လိုအပ်သည်၊ ထို့ကြောင့် ပထမအကွက်တွင် အမှီအခိုကင်းသော ကိန်းရှင် X ၏ တန်ဖိုးများသာ ရှိပြီး ဒုတိယအကွက်တွင် မှီခိုနေသော ကိန်းရှင် Y ၏ တန်ဖိုးများသာ ရှိနေမည်ဖြစ်သည်။

ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။

ရိုးရှင်းပြီး မျဉ်းကြောင်းမျိုးစုံ ဆုတ်ယုတ်မှု

နောက်ဆုံးတွင်၊ ၎င်းတို့သည် စာရင်းဇယားများတွင် အသုံးပြုလေ့ရှိသော linear regression အမျိုးအစားနှစ်မျိုးဖြစ်သောကြောင့် ရိုးရှင်းသော linear regression နှင့် multiple linear regression အကြား ကွာခြားချက်ကို ကျွန်ုပ်တို့တွေ့ရပါမည်။

မျဉ်းကြောင်းကြောင်း ဆုတ်ယုတ်မှု အများအပြား သည် တုံ့ပြန်မှု ကိန်းရှင်တစ်ခုသို့ နှစ်ခု သို့မဟုတ် ထို့ထက်ပိုသော ရှင်းပြနိုင်သော ကိန်းရှင်များကို သင်္ချာနည်းဖြင့် ချိတ်ဆက်နိုင်စေသည်။ ဆိုလိုသည်မှာ၊ မျဉ်းကြောင်း ဆုတ်ယုတ်မှု အများအပြားတွင်၊ အမှီအခိုကင်းသော ကိန်းရှင်နှစ်ခု အနည်းဆုံးရှိသည့် မော်ဒယ်တစ်ခုကို ဖန်တီးထားသည်။

ထို့ကြောင့်၊ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုနှင့် မျဉ်းဖြောင့်ဆုတ်ယုတ်မှုကြားခြားနားချက် မှာ သီးခြားကိန်းရှင်အရေအတွက်ဖြစ်သည်။ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုတွင်၊ သီးခြားကိန်းရှင်တစ်ခုသာရှိသော်လည်း၊ မျဉ်းကြောင်းနှိုင်းယှဥ်မှုအများအပြားတွင် သီးခြားကွဲလွဲချက်နှစ်ခု သို့မဟုတ် ထို့ထက်ပိုသော သီးခြားကိန်းရှင်များရှိသည်။

➤ ကြည့်ပါ- မျဉ်းကြောင်းမျိုးစုံ ဆုတ်ယုတ်မှု

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။