အကျိုးသက်ရောက်မှုအရွယ်အစား- ၎င်းသည် ဘာလဲ၊ အဘယ်ကြောင့် အရေးကြီးသနည်း။
“စာရင်းအင်းဆိုင်ရာ အရေးပါမှုက ရလဒ်တွေနဲ့ ပတ်သက်ပြီး စိတ်ဝင်စားစရာ အနည်းဆုံးပါပဲ။ ပြင်းအားအစီအမံများ၏ ရလဒ်များကို ဖော်ပြရန် လိုအပ်သည် – ကုသမှုသည် လူများကို ထိခိုက်စေရုံသာမက ၎င်းတို့ကို မည်မျှအကျိုးသက်ရောက်စေသည်ကို ဖော်ပြပါ။ -Gene V. Glass
စာရင်းဇယားများတွင်၊ ကျွန်ုပ်တို့သည် အုပ်စုနှစ်ခုကြားတွင် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားချက်ရှိမရှိ ဆုံးဖြတ်ရန် p-values ကို အသုံးပြုလေ့ရှိသည်။
ဥပမာအားဖြင့်၊ မတူညီသော လေ့လာမှုနည်းပညာနှစ်ခုသည် မတူညီသော စာမေးပွဲရမှတ်များကို ဖြစ်ပေါ်စေသည်ဆိုကြပါစို့။ ထို့ကြောင့်၊ ကျွန်ုပ်တို့တွင် စာမေးပွဲတစ်ခုအတွက် ပြင်ဆင်ရန် လေ့လာမှုတစ်ခုအတွက် လေ့လာမှုနည်းပညာကို အသုံးပြုနေသည့် ကျောင်းသား အယောက် 20 အုပ်စုရှိပြီး အခြားကျောင်းသား 20 အုပ်စုသည် မတူညီသော လေ့လာမှုနည်းပညာကို အသုံးပြုနေကြပါသည်။ ထို့နောက် ကျောင်းသားတစ်ဦးစီအား တူညီသော စာမေးပွဲကို ပေးသည်။
အဓိပ္ပါယ်များတွင် ခြားနားချက်ကို ဆုံးဖြတ်ရန် နမူနာနှစ်ခု t-test ကို run ပြီးနောက်၊ စာမေးပွဲအတွက် p-value သည် 0.001 ဖြစ်ကြောင်း တွေ့ရှိရပါသည်။ ကျွန်ုပ်တို့သည် 0.05 ၏ အရေးပါမှုအဆင့်ကို အသုံးပြုပါက၊ ၎င်းသည် အုပ်စုနှစ်ခု၏ ပျမ်းမျှရလဒ်များကြားတွင် ကိန်းဂဏန်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားချက်ကို ဆိုလိုသည်။ ထို့ကြောင့် လေ့လာမှုနည်းပညာသည် စမ်းသပ်မှုရလဒ်များအပေါ် သက်ရောက်မှုရှိသည်။
သို့သော်၊ p-value သည် လေ့လာခြင်းနည်းပညာသည် စာမေးပွဲရမှတ်များအပေါ် သက်ရောက်မှုရှိကြောင်း ကျွန်ုပ်တို့ကိုပြောပြသော်လည်း ထိုသက်ရောက်မှု၏ အတိုင်းအတာ ကို ကျွန်ုပ်တို့အား မပြောပြပါ။ ဒါကိုနားလည်ဖို့ အကျိုးသက်ရောက်မှု အရွယ်အစားကို သိဖို့လိုပါတယ်။
သက်ရောက်မှုအရွယ်အစားကဘာလဲ။
အကျိုးသက်ရောက်မှုအရွယ်အစား သည် အုပ်စုနှစ်ခုကြားရှိ ကွာခြားချက်ကို တွက်ချက်ရန် နည်းလမ်းတစ်ခုဖြစ်သည်။
p-value သည် အုပ်စုနှစ်ခုကြားတွင် ကိန်းဂဏန်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားချက် ရှိ/မရှိကို ပြောပြနိုင်သော်လည်း အကျိုးသက်ရောက်မှု အရွယ်အစားက ထိုကွာခြားချက် အမှန်တကယ် မည်မျှကြီးမား သည်ကို ပြောပြနိုင်သည်။ လက်တွေ့တွင်၊ အကျိုးသက်ရောက်မှုအရွယ်အစားများသည် p-တန်ဖိုးများထက် သိရန် ပို၍စိတ်ဝင်စားစရာကောင်းပြီး အသုံးဝင်ပါသည်။
သင်လုပ်ဆောင်နေသော ခွဲခြမ်းစိတ်ဖြာမှုအမျိုးအစားပေါ်မူတည်၍ အကျိုးသက်ရောက်မှုအရွယ်အစားကို တိုင်းတာရန် နည်းလမ်းသုံးမျိုးရှိပါသည်။
1. Standardized ဆိုသည်မှာ ခြားနားချက်
အုပ်စုနှစ်ခုကြားရှိ ပျမ်းမျှကွာခြားချက်ကို လေ့လာလိုသောအခါ၊ အကျိုးသက်ရောက်မှုအရွယ်အစားကို တွက်ချက်ရန် သင့်လျော်သောနည်းလမ်းမှာ စံသတ်မှတ်ထားသော ပျမ်းမျှကွာခြားချက်ကို အသုံးပြုခြင်းဖြစ်သည်။ အသုံးပြုရန် ရေပန်းအစားဆုံး ဖော်မြူလာကို Cohen’s d ဟုခေါ်ပြီး အောက်ပါအတိုင်း တွက်ချက်သည်။
Cohen ၏ D = ( x1 – x2 )/ s
x 1 နှင့် x 2 တို့သည် အုပ်စု 1 နှင့် အုပ်စု 2 ၏နမူနာနည်းလမ်းများဖြစ်ပြီး s သည် အုပ်စုနှစ်စုကို ရေးဆွဲခဲ့သည့် လူဦးရေ၏စံသွေဖည်မှုဖြစ်သည်။
ဤဖော်မြူလာကို အသုံးပြု၍ အကျိုးသက်ရောက်မှုအရွယ်အစားသည် အဓိပ္ပာယ်ဖွင့်ဆိုရန် လွယ်ကူသည်-
- d of 1 သည် အုပ်စုနှစ်ခု၏ အဓိပ္ပါယ်မှာ စံသွေဖည်မှုတစ်ခုဖြင့် ကွဲပြားသည်ကို ဖော်ပြသည်။
- d of 2 ဆိုသည်မှာ အုပ်စုဟူသည် စံသွေဖည်နှစ်ချက်ဖြင့် ကွဲပြားသည်။
- d ၏ 2.5 သည် ၎င်းတို့နှစ်ခု၏ အဓိပ္ပါယ်မှာ 2.5 စံသွေဖည်မှုများဖြင့် ကွဲပြားသည်ကို ညွှန်ပြပါသည်။
အကျိုးသက်ရောက်မှုအရွယ်အစားကို အဓိပ္ပာယ်ဖွင့်ဆိုရန် အခြားနည်းလမ်းမှာ- အကျိုးသက်ရောက်မှုအရွယ်အစား 0.3 ဆိုသည်မှာ အုပ်စု 2 ရှိ ပျမ်းမျှလူ၏ရမှတ်သည် အုပ်စု 1 ၏လူပျမ်းမျှထက် 0.3 စံသွေဖည်မှုများဖြစ်ပြီး ထို့ကြောင့် အုပ်စု 1 ၏ ရမှတ်များ၏ 62% ကျော်လွန်နေပါသည်။ .
အောက်ပါဇယားသည် မတူညီသောအကျိုးသက်ရောက်မှုအရွယ်အစားနှင့် ၎င်းတို့၏သက်ဆိုင်ရာရာခိုင်နှုန်းများကိုပြသသည်-
| သက်ရောက်မှုအရွယ်အစား | အုပ်စု 2 ၏ ရာခိုင်နှုန်းသည် အုပ်စု 1 ရှိ လူများ၏ ပျမ်းမျှအောက် ဖြစ်လိမ့်မည်။ |
|---|---|
| ၀.၀ | 50% |
| ၀.၂ | 58% |
| ၀.၄ | 66% |
| ၀.၆ | 73% |
| ၀.၈ | 79% |
| ၁.၀ | ၈၄% |
| ၁.၂ | 88% |
| ၁.၄ | ၉၂% |
| ၁.၆ | ၉၅% |
| ၁.၈ | ၉၆% |
| 2.0 | 98% |
| ၂.၅ | 99% |
| ၃.၀ | 99.9% |
အကျိုးသက်ရောက်မှုအရွယ်အစား ပိုကြီးလေ၊ အုပ်စုတစ်ခုစီရှိ ပျမ်းမျှလူတစ်ဦးချင်းအကြား ကွာခြားမှု ပိုများလေဖြစ်သည်။
ယေဘူယျအားဖြင့်၊ 0.2 သို့မဟုတ် ထို့ထက်နည်းသော d ကို သေးငယ်သောအကျိုးသက်ရောက်မှုအရွယ်အစားဟုယူဆသည်၊ d သည် 0.5 ဝန်းကျင်ကို အလယ်အလတ်အကျိုးသက်ရောက်မှုအရွယ်အစားအဖြစ်သတ်မှတ်ထားပြီး d ကို 0.8 သို့မဟုတ် ထို့ထက်ကြီးမားသောအကျိုးသက်ရောက်မှုအရွယ်အစားအဖြစ်သတ်မှတ်သည်။
ထို့ကြောင့်၊ အုပ်စုနှစ်ခု၏ အဓိပ္ပါယ်မှာ အနည်းဆုံး 0.2 စံသွေဖည်မှုများဖြင့် မကွဲပြားပါက p-value သည် ကိန်းဂဏန်းအရ သိသာထင်ရှားသော်လည်း ကွာခြားချက်မှာ အရေးမပါပါ။
2. ဆက်စပ်ကိန်း
variable နှစ်ခုကြားရှိ အရေအတွက်ဆိုင်ရာ ဆက်နွယ်မှုကို လေ့လာလိုသောအခါ၊ အကျိုးသက်ရောက်မှုအရွယ်အစားကို တွက်ချက်ရန် အတွေ့ရအများဆုံးနည်းလမ်းမှာ Pearson correlation coefficient ကို အသုံးပြုခြင်းဖြစ်သည်။ ၎င်းသည် ကိန်းရှင် X နှင့် Y နှစ်ခုကြားရှိ မျဉ်းကြောင်းဆက်စပ်မှုကို တိုင်းတာမှုတစ်ခုဖြစ်သည်။ ၎င်းတွင် -1 နှင့် 1 အကြား တန်ဖိုးတစ်ခုရှိသည်။
- -1 သည် ကိန်းရှင်နှစ်ခုကြားတွင် လုံးဝအပျက်သဘောဆောင်သော ဆက်စပ်ဆက်နွယ်မှုကို ညွှန်ပြသည်။
- 0 သည် variable နှစ်ခုကြားတွင် linear ဆက်စပ်မှုမရှိဟု ညွှန်ပြသည်။
- 1 သည် ကိန်းရှင်နှစ်ခုကြားတွင် လုံးဝအပြုသဘောဆောင်သောမျဉ်းကြောင်းဆက်စပ်မှုကို ညွှန်ပြသည်။
Pearson ဆက်စပ်ကိန်းကို တွက်ချက်ရန် ဖော်မြူလာသည် ရှုပ်ထွေးသော်လည်း စိတ်ဝင်စားသူများအတွက် ဤနေရာတွင် ရှာတွေ့နိုင်ပါသည်။
နောက်ထပ်ဆက်စပ်မှုကိန်းဂဏန်းသည် သုညမှဖြစ်ပြီး၊ ကိန်းရှင်နှစ်ခုကြားရှိ မျဉ်းကြောင်းဆက်နွယ်မှု အားကောင်းလေဖြစ်သည်။ ကိန်းရှင် X နှင့် Y တို့၏ တန်ဖိုးများကို ရိုးရှင်းသော အပိုင်းအစတစ်ခု ဖန်တီးခြင်းဖြင့်လည်း တွေ့မြင်နိုင်သည်။
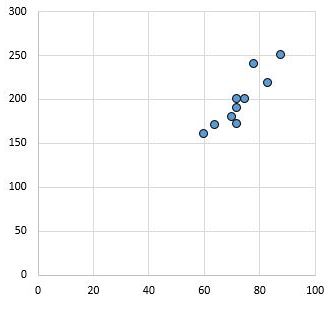
ဥပမာအားဖြင့်၊ အောက်ပါ scatterplot သည် ဆက်စပ်ကိန်း r = 0.94 ဖြင့် ကိန်းရှင်နှစ်ခု၏ တန်ဖိုးများကို ပြသသည်။
ဤတန်ဖိုးသည် သုညနှင့် ဝေးသည်၊၊ ကိန်းရှင်နှစ်ခုကြားတွင် ခိုင်မာသော အပြုသဘောဆောင်သော ဆက်ဆံရေးရှိကြောင်း ညွှန်ပြသည်။
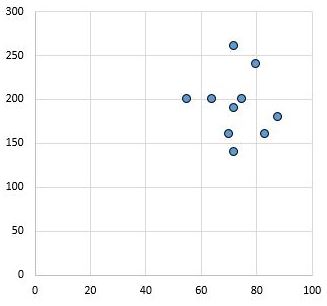
အပြန်အလှန်အားဖြင့်၊ အောက်ပါ scatterplot သည် r = 0.03 ၏ ဆက်စပ်ကိန်းပါသော ကိန်းရှင်နှစ်ခု၏ တန်ဖိုးများကို ပြသသည်။ ဤတန်ဖိုးသည် သုညနှင့် နီးကပ်နေပြီး၊ ကိန်းရှင်နှစ်ခုကြားတွင် ဆက်စပ်မှုမရှိကြောင်း ညွှန်ပြသည်။
ယေဘူယျအားဖြင့်၊ Pearson ဆက်စပ်ကိန်းဂဏန်း r ၏တန်ဖိုးသည် 0.1 ခန့်၊ အလယ်အလတ်ဖြစ်လျှင် 0.3 နှင့် r ညီမျှခြင်း သို့မဟုတ် 0.5 နှင့် ကြီးပါက ကြီးမားလျှင် အကျိုးသက်ရောက်မှုအရွယ်အစားကို သေးငယ်သည်ဟု ယူဆပါသည် ။
3. Odds အချိုး
ထိန်းချုပ်မှုအုပ်စုတစ်ခုရှိ အောင်မြင်မှုမသာမယာများနှင့် ကုသရေးအုပ်စုတစ်ခုရှိ အောင်မြင်မှုမတူညီမှုများကို လေ့လာလိုပါက အကျိုးသက်ရောက်မှုအရွယ်အစားကို တွက်ချက်ရန် အတွေ့ရအများဆုံးနည်းလမ်းမှာ မသာမယာအချိုးကို အသုံးပြုခြင်းဖြစ်သည်။
ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့တွင် အောက်ပါဇယားရှိသည် ဆိုပါစို့။
| သက်ရောက်မှုအရွယ်အစား | #အောင်မြင်ပါစေ။ | #စစ်တုရင်ကစားနည်း |
|---|---|---|
| ကုသရေးအဖွဲ့ | ရှိသည် | ခ |
| ထိန်းချုပ်ရေးအဖွဲ့ | VS | ဃ |
ပေါက်ကြားမှုအချိုးကို အောက်ပါအတိုင်း တွက်ချက်ပါမည်။
အချိုးအစား = (AD) / (BC)
ထပ်လောင်းအချိုးအစားသည် 1 မှဖြစ်လေလေ၊ ကုသမှုသည် အမှန်တကယ်အကျိုးသက်ရောက်မှုရှိစေမည့် ဖြစ်နိုင်ခြေပိုများလေဖြစ်သည်။
P-Values များထက် Effect Size ကို အသုံးပြုခြင်း၏ အကျိုးကျေးဇူးများ
အကျိုးသက်ရောက်မှုအရွယ်အစားများသည် p-တန်ဖိုးများထက် အားသာချက်များစွာရှိသည်။
1. အကျိုးသက်ရောက်မှုအရွယ်အစားသည် အုပ်စုနှစ်စုကြား ကွာခြားချက် မည်မျှကြီးမား သည် သို့မဟုတ် အုပ်စုနှစ်ခုကြားတွင် ပေါင်းသင်းမှု မည်မျှပြင်းထန် ကြောင်း ပိုမိုကောင်းမွန်သော အကြံဥာဏ်ကိုရရှိစေပါသည်။ p-value သည် သိသာထင်ရှားသော ခြားနားချက် သို့မဟုတ် သိသာထင်ရှားသော ဆက်စပ်မှု ရှိ ၊ မရှိ ကျွန်ုပ်တို့ကိုသာ ပြောပြနိုင်သည်။
2. p-တန်ဖိုးများနှင့် မတူဘဲ၊ မတူညီသော ဆက်တင်များတွင် ပြုလုပ်ခဲ့သော မတူညီသော လေ့လာမှုများ၏ ရလဒ်များကို အရေအတွက်အားဖြင့် နှိုင်းယှဉ်ရန်အတွက် အကျိုးသက်ရောက်မှု အရွယ်အစားများကို အသုံးပြုနိုင်သည်။ ဤအကြောင်းကြောင့်၊ မက်တာခွဲခြမ်းစိတ်ဖြာမှုတွင် အကျိုးသက်ရောက်မှုအရွယ်အစားများကို မကြာခဏအသုံးပြုသည်။
3. P တန်ဖိုးများသည် ကြီးမားသောနမူနာအရွယ်အစားများဖြင့် သက်ရောက်မှုရှိနိုင်သည်။ နမူနာအရွယ်အစား ပိုကြီးလေ၊ အယူအဆစမ်းသပ်မှုတစ်ခု၏ ကိန်းဂဏန်းဆိုင်ရာ စွမ်းအား ကြီးမားလေလေ၊ ၎င်းအား သေးငယ်သော အကျိုးသက်ရောက်မှုများကိုပင် သိရှိနိုင်စေမည်ဖြစ်သည်။ ၎င်းသည် လက်တွေ့ကျသော အရေးပါမှု မရှိနိုင်သည့် သေးငယ်သော အကျိုးသက်ရောက်မှု အရွယ်အစားများကြားမှ p-တန်ဖိုးများ နိမ့်ပါးသွားနိုင်သည်။
ရိုးရှင်းသောဥပမာတစ်ခုသည် ယင်းကိုရှင်းလင်းစွာဖော်ပြနိုင်သည်- လေ့လာမှုနည်းပညာနှစ်ခုသည် မတူညီသောစမ်းသပ်မှုရမှတ်များဆီသို့ ဦးတည်သွားခြင်းရှိမရှိ သိလိုသည်ဆိုပါစို့။ ကျွန်ုပ်တို့တွင် ကျောင်းသား 20 ရှိသောအုပ်စုတွင် လေ့လာမှုနည်းစနစ်တစ်ခုအသုံးပြုပြီး အခြားကျောင်းသား 20 အုပ်စုမှ မတူညီသောလေ့လာမှုနည်းပညာကိုအသုံးပြုပါသည်။ ထို့နောက် ကျောင်းသားတစ်ဦးစီအား တူညီသော စာမေးပွဲကို ပေးသည်။
အုပ်စု 1 ၏ ပျမ်းမျှရမှတ်မှာ 90.65 ဖြစ်ပြီး အုပ်စု 2 ၏ ပျမ်းမျှရမှတ်မှာ 90.75 ဖြစ်သည်။ နမူနာ 1 အတွက် စံသွေဖည်မှုသည် 2.77 ဖြစ်ပြီး နမူနာ 2 အတွက် စံသွေဖည်မှုသည် 2.78 ဖြစ်သည်။
အမှီအခိုကင်းသောနမူနာနှစ်ခု t-test ကို ကျွန်ုပ်တို့လုပ်ဆောင်သောအခါ၊ စမ်းသပ်မှုစာရင်းအင်းသည် -0.113 ဖြစ်ပြီး သက်ဆိုင်ရာ p-တန်ဖိုးသည် 0.91 ဖြစ်သည်ကို တွေ့ရှိရသည်။ ပျမ်းမျှ စာမေးပွဲရမှတ်များအကြား ကွာခြားချက်မှာ ကိန်းဂဏန်းအရ သိသာထင်ရှားခြင်း မရှိပါ။
သို့သော် နမူနာနှစ်ခု၏နမူနာအရွယ်အစားမှာ 200 ဖြစ်သည်ဆိုပါက သုံးသပ်ပါ၊ သို့သော် အဓိပ္ပါယ်နှင့်စံသွေဖည်မှုများမှာ အတိအကျတူညီနေပါသည်။
ဤကိစ္စတွင်၊ သီးခြားနမူနာနှစ်ခု t-test သည် စမ်းသပ်မှုစာရင်းအင်းသည် -1.97 ဖြစ်ပြီး သက်ဆိုင်ရာ p-value သည် 0.05 အောက်တွင်သာရှိကြောင်း ပြသမည်ဖြစ်သည်။ ပျမ်းမျှစာမေးပွဲရမှတ်များအကြား ကွာခြားချက်မှာ ကိန်းဂဏန်းအရ သိသာထင်ရှားပါသည်။
ကြီးမားသောနမူနာအရွယ်အစားများသည် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ကောက်ချက်များအား ဖြစ်ပေါ်စေနိုင်သည့် အရင်းခံအကြောင်းရင်းမှာ t -test ကိန်းဂဏန်းများကို တွက်ချက်ရန် အသုံးပြုသည့် ဖော်မြူလာကြောင့်ဖြစ်သည်-
စမ်းသပ်စာရင်းအင်း t = [( x 1 – x 2 ) – d ] / (√ s 2 1 / n 1 + s 2 2 / n 2 )
n 1 နှင့် n 2 သည် သေးငယ်သောအခါ t -test statistic ၏ integer ပိုင်းခြေသည် သေးငယ်ကြောင်း သတိပြုပါ။ ဂဏန်းငယ်ဖြင့် ခွဲလိုက်သောအခါတွင် ဂဏန်းကြီးတစ်ခုရသွားပါသည်။ ဆိုလိုသည်မှာ t- test statistic သည် ကြီးမားမည်ဖြစ်ပြီး သက်ဆိုင်ရာ p-value သည် သေးငယ်မည်ဖြစ်ပြီး၊ ထို့ကြောင့် ကိန်းဂဏန်းဆိုင်ရာ သိသာထင်ရှားသောရလဒ်များကို ရရှိစေမည်ဖြစ်သည်။
ကောင်းသောအကျိုးသက်ရောက်မှုအရွယ်အစားကိုမည်သို့ယူဆသနည်း။
ကျောင်းသားတွေ မကြာခဏမေးလေ့ရှိတဲ့ မေးခွန်းတစ်ခုကတော့ ကောင်းမွန်တဲ့ အကျိုးသက်ရောက်မှု အရွယ်အစားကို ဘယ်အရာလို့ သတ်မှတ်ပါသလဲ။
အတိုကောက် အဖြေ- အုပ်စုနှစ်စုကြား ကွာခြားချက် သို့မဟုတ် အုပ်စုနှစ်စုကြား ပေါင်းစည်းမှု အင်အားကို ရိုးရှင်းစွာ တိုင်းတာသောကြောင့် အကျိုးသက်ရောက်မှု အရွယ်အစားသည် “ ကောင်း” သို့မဟုတ် “ ဆိုး” မဖြစ်ရပါ။
သို့သော်၊ အကျိုးသက်ရောက်မှုတစ်ခု၏ ပြင်းအားသည် သေးငယ်သည်၊ အလတ် သို့မဟုတ် ကြီးမားခြင်းရှိ၊
Cohen ၏ D:
- 0.2 သို့မဟုတ် ထို့ထက်နည်းသော d ကို သေးငယ်သောအကျိုးသက်ရောက်မှုအရွယ်အစားအဖြစ် သတ်မှတ်သည်။
- 0.5 ၏ d ကို အလယ်အလတ်အကျိုးသက်ရောက်မှုအရွယ်အစားအဖြစ် သတ်မှတ်သည်။
- 0.8 သို့မဟုတ် ထို့ထက်ပို၍ d ကို ကြီးမားသောအကျိုးသက်ရောက်မှုအရွယ်အစားအဖြစ် သတ်မှတ်သည်။
Pearson Correlation Coefficient
- 0.1 ဝန်းကျင် r ၏ ပကတိတန်ဖိုးကို သေးငယ်သောအကျိုးသက်ရောက်မှုအရွယ်အစားအဖြစ်သတ်မှတ်သည်။
- 0.3 ဝန်းကျင် r ၏ ပကတိတန်ဖိုးကို အလယ်အလတ်အကျိုးသက်ရောက်မှုအရွယ်အစားအဖြစ် သတ်မှတ်သည်။
- r 0.5 ထက်ကြီးသော ပကတိတန်ဖိုးကို ကြီးမားသောအကျိုးသက်ရောက်မှုအရွယ်အစားအဖြစ် သတ်မှတ်သည်။
သို့သော်၊ “ ခိုင်မာသော” ဆက်စပ်မှု၏အဓိပ္ပါယ်ဖွင့်ဆိုချက်သည် နယ်ပယ်တစ်ခုမှတစ်ခုသို့ ကွဲပြားနိုင်သည်။ မတူညီသောစက်မှုလုပ်ငန်းများတွင် ခိုင်မာသောဆက်စပ်မှုဟုယူဆသောအရာကို ပိုမိုကောင်းမွန်စွာနားလည်ရန် ဤဆောင်းပါးကို ကိုးကားပါ။