အချိုးအစားအတွက် ယုံကြည်မှုကြားကာလ

အားဖြင့် ဩဂုတ် 3, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် အချိုးအတွက် ယုံကြည်မှုကြားကာလသည် မည်သည်နှင့် ၎င်းကို စာရင်းအင်းများတွင် အသုံးပြုကြောင်း ရှင်းပြထားသည်။ အလားတူပင်၊ အချိုး၏ယုံကြည်မှုကြားကာလကို တွက်ချက်နည်းနှင့် သဘောတရားကို ပိုမိုနားလည်ရန် ဖြေရှင်းထားသော လေ့ကျင့်ခန်းတစ်ခုကို သင်ရှာဖွေတွေ့ရှိမည်ဖြစ်သည်။

အချိုးအစား၏ ယုံကြည်မှုကြားကာလသည် အဘယ်နည်း။

အချိုးအစားအတွက် ယုံကြည်မှုကြားကာလ သည် လူဦးရေအချိုးအစားအတွက် လက်ခံနိုင်သောတန်ဖိုးများအကွာအဝေးကို ပံ့ပိုးပေးသော ကြားကာလတစ်ခုဖြစ်သည်။ ဆိုလိုသည်မှာ၊ အချိုးအတွက် ယုံကြည်မှုကြားကာလသည် အမြင့်ဆုံးတန်ဖိုးနှင့် လူဦးရေအချိုးသည် အမှား၏အနားသတ်ဖြင့် တည်ရှိသည့် အနိမ့်ဆုံးတန်ဖိုးကို ညွှန်ပြသည်။

ဥပမာအားဖြင့်၊ ယုံကြည်မှုအဆင့် 95% ရှိသော လူဦးရေအချိုးအတွက် ယုံကြည်မှုကြားကာလသည် (0.73၊ 0.81) ဖြစ်ပါက၊ ဆိုလိုသည်မှာ လူဦးရေအချိုးအစားသည် 73% နှင့် 81% ကြားဖြစ်နိုင်ခြေ 95% ဖြစ်သည်။

ထို့ကြောင့်၊ အချို့သောဝိသေသလက္ခဏာများနှင့် ကိုက်ညီသော လူဦးရေအချိုးအစား၏တန်ဖိုးကို ခန့်မှန်းရန် အချိုးအစား၏ ယုံကြည်မှုကြားကာလကို အသုံးပြုပါသည်။

နောက်အပိုင်းတွင်ကျွန်ုပ်တို့မြင်ရမည့်အတိုင်း၊ အချိုးအတွက်ယုံကြည်မှုကြားကာလသည်နမူနာအချိုးအစားနှင့်နမူနာရှိလေ့လာတွေ့ရှိချက်အရေအတွက်ပေါ်တွင်မူတည်ပါသည်။

အချိုးအစားအတွက် ယုံကြည်မှု ကြားကာလ ဖော်မြူလာ

အချိုးအတွက် ယုံကြည်မှုကြားကာလကို Z α/2 ၏ တန်ဖိုးကို နမူနာအချိုးအစား (p) ဖြင့် မြှောက်ပြီး 1-p ဖြင့် မြှောက်ကာ နမူနာအရွယ်အစား (n) ဖြင့် ပိုင်းခြားခြင်းဖြင့် တွက်ချက်သည်။ ထို့ကြောင့် အချိုးအစားအတွက် ယုံကြည်မှုကြားကာလကို တွက်ချက်ရန် ဖော်မြူလာ မှာ-

\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)

ရွှေ-

  • p

    နမူနာအချိုးဖြစ်သည်။

  • n

    နမူနာအရွယ်အစားဖြစ်သည်။

  • Z_{\alpha/2}

    α/2 ၏ဖြစ်နိုင်ခြေနှင့် သက်ဆိုင်သော စံပုံမှန်ဖြန့်ဝေမှု၏ အရေအတွက်ဖြစ်သည်။ ကြီးမားသောနမူနာအရွယ်အစားများနှင့် 95% ယုံကြည်မှုအဆင့်အတွက် ၎င်းသည် များသောအားဖြင့် 1.96 နှင့် နီးစပ်ပြီး 99% ယုံကြည်မှုအဆင့်အတွက် ၎င်းသည် များသောအားဖြင့် 2.576 နှင့် နီးစပ်ပါသည်။

အချိုးအတွက် ယုံကြည်မှုကြားကာလကို တွက်ချက်ခြင်း ဥပမာ

အချိုးအစားအတွက် ယုံကြည်မှုကြားကာလကို မည်ကဲ့သို့ တွက်ချက်သည်ကို သင်မြင်နိုင်စေရန်၊ ကျွန်ုပ်တို့သည် သင့်အား အောက်တွင် ခိုင်မာသော ဥပမာတစ်ဆင့်ပြီးတစ်ဆင့် ထားခဲ့ပါ။

  • အာမခံကုမ္ပဏီတစ်ခုသည် စျေးကွက်သုတေသနပြုလုပ်ပြီး နိုင်ငံတစ်နိုင်ငံတွင် လူမည်မျှအသက်အာမခံရှိသည်ကို ဆုံးဖြတ်လိုပါသည်။ ဒီလိုလုပ်ဖို့ လူ 700 ကို ကျပန်းနမူနာကို ခွဲခြမ်းစိတ်ဖြာပြီး နမူနာရဲ့ 40% မှာ အသက်အာမခံရှိတယ်လို့ နိဂုံးချုပ်ပါတယ်။ နိုင်ငံ့လူဦးရေအချိုးအတွက် 95% ယုံကြည်မှုအဆင့်မှာ ယုံကြည်မှုကြားကာလက ဘယ်လောက်လဲ။

လူဦးရေအချိုးအစား၏ ယုံကြည်မှုကြားကာလကို ဆုံးဖြတ်ရန်၊ အထက်ဖော်ပြပါ ပုံသေနည်းကို အသုံးပြုရန် လိုအပ်သည်-

\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)

ဤကိစ္စတွင်၊ ကျွန်ုပ်တို့သည် ယုံကြည်မှုကြားကာလ၏ ယုံကြည်မှုအဆင့်ကို 95% ဖြစ်စေလိုသောကြောင့် ကျွန်ုပ်တို့ယူရန်လိုအပ်သည့် Z α/2 တန်ဖိုးသည် 1.96 ဖြစ်သည်။

1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025

\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}

ပြဿနာထုတ်ပြန်ချက်တွင်နမူနာအရွယ်အစားမှာ n=700 ဖြစ်ပြီး နမူနာတွင်တွေ့ရှိရသောအချိုးအစားမှာ p=0.40 ဖြစ်ပြီး၊ ထို့ကြောင့် ကျွန်ုပ်တို့သည် ဒေတာကို အချိုးအစားအတွက် ယုံကြည်မှုကြားကာလဖော်မြူလာအဖြစ် အစားထိုးပြီး ကြားကာလ၏ကန့်သတ်ချက်များကို တွက်ချက်ပါ-

\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)

\displaystyle \left(0,40-1,96\cdot \sqrt{\frac{0,40\cdot (1-0,40)}{700}}\ , \ 0,40+1,96\cdot \sqrt{\frac{0,40\cdot (1-0,40)}{700}\right)

\displaystyle \left(0,36 \ , \ 0,44\right)

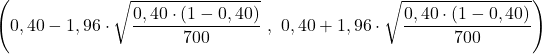
နိဂုံးချုပ်အားဖြင့်၊ လေ့လာခဲ့သည့် လူဦးရေအချိုးအစားမှာ ၃၆% နှင့် ၄၄% ကြားတွင် ယုံကြည်မှုအဆင့် ၉၅% ဖြစ်သည်။

စာရေးသူအကြောင်း

Benjamin Anderson
Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။

မှတ်ချက်တစ်ခုထည့်ပါ။

သင့် email လိပ်စာကို ဖော်ပြမည် မဟုတ်ပါ။ လိုအပ်သော ကွက်လပ်များကို * ဖြင့်မှတ်သားထားသည်