အောက်စတုရန်းများ
ဤဆောင်းပါးတွင် ကိန်းဂဏန်းစာရင်းဇယားများတွင် အနိမ့်ဆုံးစတုရန်းများပါဝင်ကြောင်း၊ အနည်းဆုံးစတုရန်းနည်းဟူသည် အဘယ်နည်းနှင့် ဆုတ်ယုတ်မှုပုံစံကို လေးထောင့်အနည်းဆုံးစံနှုန်းဖြင့် တပ်ဆင်ပုံကို ရှင်းပြထားသည်။
လေးထောင့်အနည်းဆုံးနည်းလမ်းက ဘာလဲ။
အနည်းဆုံး စတုရန်းနည်း သည် ဆုတ်ယုတ်ခြင်း၏ညီမျှခြင်းကို ဆုံးဖြတ်ရန် အသုံးပြုသည့် ကိန်းဂဏန်းဆိုင်ရာ နည်းလမ်းတစ်ခုဖြစ်သည်။ တစ်နည်းဆိုရသော်၊ အနည်းဆုံးစတုရန်းနည်းသည် ဆုတ်ယုတ်မှုညီမျှခြင်းကို တွက်ချက်ရာတွင် ရရှိသောအမှားကို လျှော့ချရန် ဆုတ်ယုတ်မှုပုံစံတွင် အသုံးပြုသည့် စံသတ်မှတ်ချက်တစ်ခုဖြစ်သည်။
အတိအကျအားဖြင့်၊ အနည်းဆုံးစတုရန်းနည်းလမ်းတွင် အကြွင်းအကျန်များ၏ နှစ်ထပ်ကိန်းများကို လျှော့နည်းစေခြင်း သို့မဟုတ် တစ်နည်းအားဖြင့် ဆုတ်ယုတ်မှုပုံစံဖြင့် ခန့်မှန်းထားသော တန်ဖိုးများနှင့် သတိပြုမိသော တန်ဖိုးများကြားရှိ ခြားနားချက်များ၏ နှစ်ထပ်ကိန်းများကို လျှော့ချခြင်းအပေါ် အခြေခံသည်။ . . အနိမ့်ဆုံး စတုရန်းစံနှုန်းဖြင့် ဆုတ်ယုတ်မှုပုံစံကို အောက်တွင် အသေးစိတ်ကြည့်ရှုပါမည်။
အနည်းဆုံး စတုရန်းပုံနည်းလမ်း၏ အဓိကအင်္ဂါရပ်မှာ သတိပြုမိသော တန်ဖိုးများနှင့် ဆုတ်ယုတ်မှုလုပ်ဆောင်မှုတို့ကြား အကြာဆုံးအကွာအဝေးများကို လျှော့ချထားသည်။ အခြားသော ဆုတ်ယုတ်မှု စံနှုန်းများနှင့် မတူဘဲ၊ အနည်းဆုံး စတုရန်းပုံနည်းလမ်းသည် သေးငယ်သော အကြွင်းအကျန်များထက် ကြီးမားသော အကြွင်းအကျန်များကို လျှော့ချရန် ပိုအရေးကြီးသည်ဟု ယူဆသည်၊ အဘယ်ကြောင့်ဆိုသော် အရေအတွက်၏ နှစ်ထပ်သည် သေးငယ်သော စတုရန်းထက် များစွာ ပိုကြီးသောကြောင့် ဖြစ်သည်။ နံပါတ်
ခန့်မှန်းချက်အမှား
အနည်းဆုံး စတုရန်းပုံ၏ သဘောတရားကို အပြည့်အဝနားလည်ရန်၊ ဆုတ်ယုတ်မှုပုံစံတစ်ခုတွင် အကြွင်းအကျန်များကို ဦးစွာရှင်းလင်းရပါမည်။ ထို့ကြောင့် ခန့်မှန်းချက်အမှားတစ်ခုသည် မည်ကဲ့သို့ တွက်ချက်ထားသည်ကို အောက်တွင် ကျွန်ုပ်တို့ မြင်တွေ့ရမည်ဖြစ်သည်။
ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ အကြွင်းအကျန် ဟုလည်းခေါ်သော ခန့်မှန်းချက်အမှား သည် ဆုတ်ယုတ်မှုပုံစံဖြင့် တပ်ဆင်ထားသော တန်ဖိုးအမှန်နှင့် တန်ဖိုးအကြား ကွာခြားချက်ဖြစ်သည်။ ထို့ကြောင့် ကိန်းဂဏန်းလက်ကျန်ကို အောက်ပါအတိုင်း တွက်ချက်သည်။
![]()
ရွှေ-
-

data ရဲ့ကျန်နေတဲ့ i ပါ။
-

ဒေတာရဲ့ တကယ့်တန်ဖိုး i ပါ။
-

ဒေတာ i အတွက် ဆုတ်ယုတ်မှုပုံစံက ပေးသောတန်ဖိုးဖြစ်သည်။
ထို့ကြောင့်၊ ဒေတာအပိုင်းတစ်ခု၏ ကျန်ရှိသောပိုကြီးလေ၊ ဆုတ်ယုတ်မှုပုံစံသည် ဤဒေတာအပိုင်းအတွက် လိုက်လျောညီထွေဖြစ်လေလေဖြစ်သည်။ ထို့ကြောင့် ကျန်ရှိသောသေးငယ်လေ၊ ၎င်း၏အမှန်တကယ်တန်ဖိုးနှင့် ခန့်မှန်းတန်ဖိုးကြားအကွာအဝေးသည် သေးငယ်လေဖြစ်သည်။
အလားတူပင်၊ ဒေတာအပိုင်းတစ်ခု၏ ကျန်ရှိနေသောအချက်သည် အပေါင်းလက္ခဏာဖြစ်ပါက၊ ဆုတ်ယုတ်မှုပုံစံသည် တန်ဖိုးအမှန်တန်ဖိုးထက်နိမ့်သောတန်ဖိုးကို ခန့်မှန်းပေးသည်ဟု ဆိုလိုသည်။ အကြွင်းအကျန်သည် အနုတ်ဖြစ်နေပါက၊ ခန့်မှန်းတန်ဖိုးသည် အမှန်တကယ်တန်ဖိုးထက် ကြီးသည်ဟု ဆိုလိုသည်။
အမှားအယွင်း လေးထောင့်များကို လျှော့ချပါ။
ကိန်းဂဏန်းစာရင်းဇယားများတွင် ကျန်ရှိနေသည်များကို ယခုကျွန်ုပ်တို့သိသောအခါ၊ error squares များကိုမည်ကဲ့သို့လျှော့ချထားသည်ကိုနားလည်ရန်ပိုမိုလွယ်ကူလာမည်ဖြစ်ပါသည်။
အမှားတစ်ခု၏စတုရန်း သည် ကျန်ရှိသောတစ်ခု၏စတုရန်းဖြစ်ပြီး၊ ထို့ကြောင့် အမှားတစ်ခု၏နှစ်ထပ်ကိန်းသည် နှစ်ခု၏ပါဝါသို့မြှင့်တင်ပေးသည့် ဆုတ်ယုတ်မှုပုံစံဖြင့် တပ်ဆင်ထားသည့်တန်ဖိုးကြား ကွာခြားချက်နှင့်ညီမျှသည်။
![]()
ရွှေ-
-
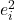
ကျန်ဒေတာ i ၏ နှစ်ထပ်ဖြစ်သည်။
-

ဒေတာရဲ့ တကယ့်တန်ဖိုး i ပါ။
-

ဒေတာ i အတွက် ဆုတ်ယုတ်မှုပုံစံက ပေးသောတန်ဖိုးဖြစ်သည်။
ထို့ကြောင့်၊ အနည်းဆုံး စတုရန်းနည်းလမ်းသည် အမှားများ၏ လေးထပ်၏ပေါင်းလဒ်ကို လျှော့ချခြင်းဖြင့် ဆုတ်ယုတ်မှုပုံစံကို ဖန်တီးခြင်း ပါဝင်သည်။ ထို့ကွောငျ့ အနဲဆုံး စတုရန်းစံသတ်မှတ်ချက်သည် အောက်ပါစကားရပ်၏ အနိမ့်ဆုံးကို အခြေခံထားခြင်းဖြစ်သည်-
![Rendered by QuickLaTeX.com \begin{array}{l} [MIN] \ \displaystyle \sum_{i=1}^ne_i^2\\[4ex][MIN] \ \displaystyle \sum_{i=1}^n(y_i-\widehat{y}_i)^2\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0a82d4d723b77093b4d584609f372cd7_l3.png)
ထို့ကြောင့် အနိမ့်ဆုံး စတုရန်းစံနှုန်းကို အနည်းဆုံး လေးထောင့်စံနှုန်းဟုလည်း ခေါ်သည်။
ယခင်ဖော်မြူလာတွင် သင်တွေ့မြင်ရသည့်အတိုင်း၊ အနည်းဆုံးစတုရန်းစံသတ်မှတ်ချက်သည် သေးငယ်သောအကြွင်းအကျန်များထက် ကြီးမားသောအကြွင်းအကျန်များကို လျှော့ချရန် ပို၍အရေးကြီးပါသည်။ ဥပမာ၊ အကြွင်းတစ်ခုသည် 3 ဖြစ်ပြီး အခြားကျန်ကြွင်းသည် 5 ဖြစ်ပါက ၎င်းတို့၏စတုရန်းများသည် 9 နှင့် 25 အသီးသီးဖြစ်ရာ အနည်းဆုံးစတုရန်းစံသတ်မှတ်ချက်သည် ပထမအကြွင်းအကျန်မတိုင်မီ ဒုတိယအကြွင်းကို ဦးစားပေးပါမည်။
လေးထောင့်အနိမ့်ဆုံး ချိန်ညှိမှု
အနည်း ဆုံး စတုရန်း စံနှုန်းကို အသုံးပြု၍ ဆုတ်ယုတ်မှု မော်ဒယ်ကို အံကိုက် ဖြည့်သွင်းခြင်းသည် အကြွင်းအကျန်များ၏ လေးထပ်များကို နည်းပါးအောင် လျှော့ချပေးသည့် ဆုတ်ယုတ်မှု ပုံစံကို ရှာဖွေခြင်း ပါဝင်သည်။ ထို့ကြောင့်၊ ဆုတ်ယုတ်မှုပုံစံမှရရှိသောညီမျှခြင်းသည် သတိပြုမိသောတန်ဖိုးများနှင့် တပ်ဆင်ထားသောတန်ဖိုးများအကြား ခြားနားချက်၏စတုရန်းများအနက် အနည်းငယ်မျှသာဖြစ်သည်။
အောက်ဖော်ပြပါ ဥပမာတွင် ဆုတ်ယုတ်မှုပုံစံကို ဖန်တီးရန် စံသတ်မှတ်ချက်များ ပိုမိုရှိနေကြောင်း သတိပြုရန်နှင့် ရွေးချယ်ထားသော စံနှုန်းပေါ်မူတည်၍ ဆုတ်ယုတ်မှုညီမျှခြင်းမှာ ကွဲပြားပါသည်။
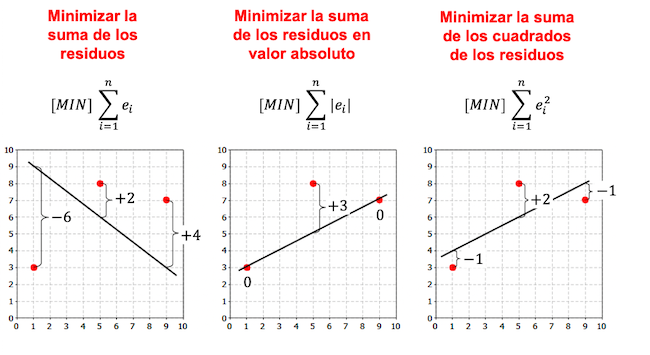
ယခင်နမူနာများတွင် သင်တွေ့မြင်ရသည့်အတိုင်း၊ တူညီသောဒေတာအတွဲအတွက် linear regression model မှရရှိသောမျဉ်းသည် ရွေးချယ်ထားသောစံနှုန်းပေါ်တွင်မူတည်ပါသည်။ ယေဘုယျအားဖြင့်၊ အနည်းဆုံးစတုရန်းစံနှုန်းကို ဆုတ်ယုတ်မှုပုံစံများတွင် အသုံးပြုသည်။
စာရင်းဇယားများတွင် အသုံးအများဆုံး ဆုတ်ယုတ်မှုပုံစံသည် မျဉ်းဖြောင့်ကို အသုံးပြု၍ အမှီအခိုကင်းသော ကိန်းရှင် X နှင့် အမှီပြုသော ကိန်းရှင် Y အကြား အနီးစပ်ဆုံး ဆက်နွယ်မှု ပါ၀င်သော ရိုးရှင်းသော မျဉ်းဖြောင့်ဆုတ်ယုတ်မှု ပုံစံဖြစ်သည်။
![]()
ထို့ကြောင့်၊ ရိုးရှင်းသော linear regression model တစ်ခုသို့ data set တစ်ခုနှင့် ကိုက်ညီရန် ဖော်မြူလာများမှာ-

![]()
အောက်ဖော်ပြပါ လင့်ခ်ကို နှိပ်ခြင်းဖြင့် လေးထောင့်အနည်းဆုံး စံသတ်မှတ်ချက်ကို အသုံးပြု၍ ရိုးရှင်းသော မျဉ်းကြောင်းဆုတ်ယုတ်မှု မော်ဒယ်ကို တွက်ချက်ပုံ နမူနာကို သင်ကြည့်ရှုနိုင်သည်-