အဖြစ်အပျက်များဆုံရာဖြစ်နိုင်ခြေ

အားဖြင့် Benjamin Anderson ဩဂုတ် 1, 2023 ဖြစ်နိုင်ခြေ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် အဖြစ်အပျက်များ၏ ဆုံဖြတ်မှု ဖြစ်နိုင်ခြေကို တွက်ချက်နည်းကို ရှင်းပြထားသည်။ ထို့ကြောင့် အဖြစ်အပျက်များ၏ ဆုံဖြတ်မှုဖြစ်နိုင်ခြေအတွက် ဖော်မြူလာက ဘာလဲ၊ ထို့အပြင် လေ့ကျင့်ခန်းများကို တစ်ဆင့်ပြီးတစ်ဆင့် ဖြေရှင်းနိုင်မည်ဖြစ်သည်။

ပွဲလမ်းဆုံဆိုတာ ဘာလဲ။

ဖြစ်နိုင်ခြေ သီအိုရီတွင်၊ အဖြစ်အပျက်များ၏ ဆုံမှတ် သည် လုပ်ဆောင်ချက်အားလုံးနှင့် တူညီသော အခြေခံ ဖြစ်ရပ်များနှင့် ပေါင်းစပ်ထားသော ဖြစ်ရပ်များ၏ လည်ပတ်မှုတစ်ခု ဖြစ်သည်။ ဆိုလိုသည်မှာ၊ A နှင့် B တို့၏ ဆုံရပ်ကို A နှင့် B သက်ဆိုင်သည့် အဖြစ်အပျက်အားလုံးက တစ်ပြိုင်နက်တည်း ဖြစ်ပေါ်လာခြင်းဖြစ်သည်။

ဖြစ်ရပ်နှစ်ခု၏ လမ်းဆုံကို သင်္ကေတ ⋂ ဖြင့် ဖော်ပြသည်။ ထို့ကြောင့် A နှင့် B တို့၏ ဆုံရပ်ကို A⋂B ဟုရေးထားသည်။

ဥပမာအားဖြင့်၊ အသေကို လှိမ့်ခြင်း၏ ကျပန်းစမ်းသပ်မှုတွင် ဖြစ်ရပ်တစ်ခုသည် ကိန်းဂဏန်းတစ်ခုကို လှိမ့်လိုက်လျှင် A={2, 4, 6} နှင့် အခြားဖြစ်ရပ်တစ်ခုမှာ သုံးထက်ကြီးသောကိန်းကို B={4, 5၊ 6 }၊ ဖြစ်ရပ်နှစ်ခု၏ လမ်းဆုံမှာ A⋂B={4၊ 6} ဖြစ်သည်။

ဖြစ်ရပ်များ၏ လမ်းဆုံဖြစ်နိုင်ခြေအတွက် ဖော်မြူလာ

ဖြစ်ရပ်နှစ်ခု၏ ဆုံစည်းခြင်း၏ဖြစ်နိုင်ခြေ သည် ပထမဖြစ်ရပ်ကို ပေးထားသည့် အခြားဖြစ်ရပ်တစ်ခုဖြစ်ပွားသည့်အချိန်များဖြစ်နိုင်ခြေနှင့် ညီမျှသည်။

ထို့ကြောင့်၊ ဖြစ်ရပ်နှစ်ခု၏ ဆုံရာဖြစ်နိုင်ခြေအတွက် ဖော်မြူလာ မှာ P(A⋂B)=P(A) P(B|A)=P(B) P(A|B) ဖြစ်သည်။

$P(A\cap B)=P(A)\cdot P(B|A)=P(B)\cdot P(A|B)$

ရွှေ-

$A$

နှင့်

$B$

ဤအရာနှစ်ခုသည် ဖြစ်ရပ်နှစ်ခုဖြစ်သည်။
$P(A\cap B)$

အဖြစ်အပျက် A နှင့် Event B တို့၏ ဆုံရာဖြစ်နိုင်ခြေဖြစ်သည်။
$P(A)$

အဖြစ်အပျက် A သည် ဖြစ်ပေါ်လာမည့် ဖြစ်နိုင်ခြေဖြစ်သည်။
$P(B|A)$

ပေးထားသော အဖြစ်အပျက် A တွင် ဖြစ်ပေါ်နေသော ဖြစ်ရပ် B ၏ အခြေအနေဆိုင်ရာ ဖြစ်နိုင်ခြေ ဖြစ်သည် ။
$P(B)$

အဖြစ်အပျက် B ဖြစ်ပေါ်လာမည့် ဖြစ်နိုင်ခြေ ဖြစ်သည် ။
$P(A|B)$

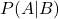
အဖြစ်အပျက် A သည် ပေးထားသော အဖြစ်အပျက် B ၏ အခြေအနေအရ ဖြစ်နိုင်ခြေ ဖြစ်သည် ။

➤ ကြည့်ပါ- အခြေအနေအရ ဖြစ်နိုင်ခြေ (သို့မဟုတ် အခြေအနေအရ ဖြစ်နိုင်ခြေ)

သို့သော်လည်း ဖြစ်ရပ်နှစ်ခုသည် သီးခြားလွတ်လပ်နေပါက၊ ဖြစ်ရပ်တစ်ခု ဖြစ်ပွားနိုင်ခြေသည် အခြားဖြစ်ရပ်တစ်ခု ဖြစ်ပွားခြင်းရှိမရှိပေါ်တွင်မူတည်မည်မဟုတ်ကြောင်း ဆိုလိုသည်။ ထို့ကြောင့် လွတ်လပ်သောဖြစ်ရပ်နှစ်ခု၏ လမ်းဆုံဖြစ်နိုင်ခြေအတွက် ပုံသေနည်းမှာ အောက်ပါအတိုင်းဖြစ်သည်။

$P(A\cap B)=P(A)\cdot P(B)$

ရွှေ-

$A$

နှင့်

$B$

ဤသည်မှာ လွတ်လပ်သောဖြစ်ရပ်နှစ်ခုဖြစ်သည်။
$P(A\cap B)$

အဖြစ်အပျက် အဖြစ်အပျက် A နှင့် အဖြစ်အပျက် B တို့၏ ဆုံရာဖြစ်နိုင်ခြေ ဖြစ်သည် ။
$P(A)$

အဖြစ်အပျက် A သည် ဖြစ်ပေါ်လာမည့် ဖြစ်နိုင်ခြေဖြစ်သည်။
$P(B)$

အဖြစ်အပျက် B ဖြစ်ပေါ်လာမည့် ဖြစ်နိုင်ခြေ ဖြစ်သည် ။

➤- လွတ်လပ်သောဖြစ်ရပ်များကို ကြည့်ပါ။

ဖြစ်ရပ်လမ်းဆုံဖြစ်နိုင်ခြေ၏ လက်တွေ့ကမ္ဘာဥပမာ

ထို့နောက်၊ အဖြစ်အပျက်နှစ်ခု၏ ဆုံစည်းမှုဖြစ်နိုင်ခြေကို တွက်ချက်ပုံကို သင်မြင်နိုင်စေရန် တစ်ဆင့်ပြီးတစ်ဆင့် ဖြေရှင်းထားသော ဥပမာနှစ်ခုကို သင့်အား ထားခဲ့ပါမည်။ အမှီအခိုကင်းသော ဖြစ်ရပ်နှစ်ခု၏ လမ်းဆုံကို ဥပမာတစ်ခုနှင့် မှီခိုနေသော ဖြစ်ရပ်နှစ်ခုကို ဦးစွာမြင်ရမည်ဖြစ်ပြီး၊ ထို့ကြောင့် ဖြစ်ရပ်နှစ်ခုလုံးကို သင်မြင်နိုင်သည်။

အမှီအခိုကင်းသော ဖြစ်ရပ်နှစ်ခု၏ ဆုံရာဖြစ်နိုင်ခြေ

သုံးကြိမ်ဆက်တိုက် သရေကျသည်။ သုံးကြိမ်စလုံးတွင် ဦးခေါင်းရရှိရန် ဖြစ်နိုင်ခြေကို ရှာပါ။

ဤကိစ္စတွင်၊ ကျွန်ုပ်တို့သည် ပူးတွဲဖြစ်နိုင်ခြေကို တွက်ချက်လိုသည့် အဖြစ်အပျက်များသည် အမှီအခိုကင်းသောကြောင့်၊ သရေရလဒ်သည် ယခင်သရေပွဲမှရရှိသောရလဒ်ပေါ်တွင်မူတည်ခြင်းမရှိသောကြောင့်ဖြစ်သည်။ ထို့ကြောင့်၊ ဆက်တိုက်ခေါင်းသုံးလုံးရနိုင်ခြေကို ဆုံးဖြတ်ရန် သီးခြားဖြစ်ရပ်များအတွက် လမ်းဆုံဖြစ်နိုင်ခြေဖော်မြူလာကို အသုံးပြုရပါမည်-

$P(A\cap B)=P(A)\cdot P(B)$

စာရေးတဲ့အခါ ဖြစ်နိုင်တဲ့ ရလဒ် နှစ်ခုပဲ ရှိတယ်၊ ခေါင်း ဒါမှမဟုတ် အမြီးတွေ ရနိုင်တယ်။ ထို့ကြောင့်၊ အကြွေစေ့ကိုပစ်သောအခါ ဦးခေါင်း သို့မဟုတ် အမြီးများရနိုင်ခြေမှာ-

$P(\text{cara})=\cfrac{1}{2}=0,5$

ထို့ကြောင့်၊ အကြွေစေ့သုံးချောင်းစလုံးတွင် ဦးခေါင်းရရှိရန် ဖြစ်နိုင်ခြေကို ရှာဖွေရန်၊ ကျွန်ုပ်တို့သည် ဦးခေါင်းရရှိရန် ဖြစ်နိုင်ခြေကို သုံးချက်မြှောက်ရန် လိုအပ်သည်-

$\begin{aligned}P(\text{cara}\cap \text{cara}\cap \text{cara})&=P(\text{cara})\cdot P(\text{cara})\cdot P(\text{cara})\\[2ex]&=0,5\cdot 0,5\cdot 0,5\\[2ex]&=0,125\end{aligned}$

အတိုချုပ်အားဖြင့်၊ ဆက်တိုက် ခေါင်းသုံးကြိမ်ရနိုင်ခြေသည် 12.5% ဖြစ်သည်။

ဖြစ်ရပ်နှစ်ခု၏ လမ်းဆုံဖြစ်နိုင်ခြေ

သေတ္တာအလွတ်တစ်ခုတွင် အပြာရောင်ဘောလုံး ၈ လုံး၊ လိမ္မော်ရောင်ဘောလုံး ၄ လုံးနှင့် အစိမ်းရောင်ဘောလုံး ၂ လုံးတို့ကို ထည့်ထားသည်။ ပထမဘောလုံးကို ပထမဘောလုံးကိုဆွဲပြီး နောက်တစ်ဘောလုံးကို ဘောက်စ်ထဲသို့ပြန်မထည့်ဘဲ ပထမဘောလုံးသည် အပြာရောင်ဖြစ်ပြီး ဒုတိယဘောလုံးသည် လိမ္မော်ရောင်ဖြစ်နိုင်ခြေအဘယ်နည်း။

ဤကိစ္စတွင်၊ ဒုတိယအဆွဲတွင် လိမ္မော်ရောင်ဘောလုံးကို ကောက်ယူနိုင်ခြေသည် ပထမအကြိမ်ဆွဲသည့်ဘောလုံး၏အရောင်ပေါ်တွင်မူတည်သောကြောင့် အဖြစ်အပျက်များသည် ဖြစ်ရပ်များအပေါ်တွင် မူတည်ပါသည်။ ထို့ကြောင့်၊ ပြဿနာက ကျွန်ုပ်တို့ကို မေးသည့် ဖြစ်နိုင်ခြေကို တွက်ချက်ရန်၊ မှီခိုဖြစ်ရပ်များအတွက် လမ်းဆုံဖြစ်နိုင်ခြေအတွက် ဖော်မြူလာကို အသုံးပြုရပါမည်-

$P(A\cap B)=P(A)\cdot P(B|A)$

ပထမအကြိမ် မဲဆွယ်ရာတွင် အပြာရောင်ဘောလုံးတစ်လုံးရရှိရန် ဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ရန် လွယ်ကူသည်၊ အပြာရောင်ဘောလုံးအရေအတွက်ကို ဘောလုံးစုစုပေါင်းအရေအတွက်ဖြင့် ပိုင်းခြားပါ။

$P(\text{bola azul})=\cfrac{8}{8+4+2}=\cfrac{8}{14}=0,57$

အခြားတစ်ဖက်တွင်၊ အပြာရောင်ဘောလုံးကိုယူပြီးနောက် လိမ္မော်ဘောလုံးတစ်လုံးဆွဲရန်ဖြစ်နိုင်ခြေကို လိမ္မော်ရောင်ဘောလုံးအရေအတွက် ကွာခြားသည့်အတွက်ကြောင့်၊ ထို့အပြင်၊ ယခုသေတ္တာအတွင်းတွင် ဘောလုံးတစ်ချောင်းလျော့နည်းသောကြောင့်၊

$P(\text{bola naranja}|\text{bola azul})=\cfrac{4}{7+4+2}=\cfrac{4}{13}=0,31$

ထို့ကြောင့်၊ အပြာရောင်ဘောလုံးကို ဦးစွာဆွဲရန်ဖြစ်နိုင်ခြေ၊ ထို့နောက်တွင်ရှိသော လိမ္မော်ဘောလုံးတစ်လုံးကို အထက်ဖော်ပြပါဖြစ်နိုင်ခြေနှစ်ခုကို မြှောက်ခြင်းဖြင့် တွက်ချက်သည်-

$\begin{array}{l}P(\text{bola azul}\cap\text{bola naranja})=\\[2ex]=P(\text{bola azul})\cdot P(\text{bola naranja}|\text{bola azul})=\\[2ex]=0,57\cdot 0,31= \\[2ex]=0,18\end{array}$

➤ ကြည့်ပါ- ဖြစ်ရပ်များ၏ ပြည်ထောင်စု၏ ဖြစ်နိုင်ခြေကို ကြည့်ပါ။

Event Intersection Properties

ဖြစ်နိုင်ခြေ သီအိုရီတွင်၊ ဖြစ်ရပ်များ၏ လမ်းဆုံတွင် အောက်ပါ ဂုဏ်သတ္တိများ ရှိသည်။

Commutative property- လမ်းဆုံဖြစ်ရပ်များ၏ အစီစဥ်သည် လုပ်ဆောင်ချက်၏ ရလဒ်ကို မပြောင်းလဲပါ။

$A\cap B=B\cap A$

Associative property- ရလဒ်သည် တူညီသောကြောင့် ဖြစ်ရပ်သုံးခု၏ လမ်းဆုံကို မည်သည့်အစီအစဥ်တွင်မဆို တွက်ချက်နိုင်သည်။

$(A\cap B)\cap C=A\cap (B\cap C)$

ဖြန့်ဖြူးမှုပိုင်ဆိုင်မှု- ဖြစ်ရပ်များ၏လမ်းဆုံသည် ဖြစ်ရပ်များသမဂ္ဂတွင် ဖြန့်ဖြူးမှုပိုင်ဆိုင်မှုကို ကျေနပ်စေသည်။

$A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$

➤ ဖြစ်ရပ်များနှင့်အတူ လုပ်ဆောင်ချက်များကို ကြည့်ပါ။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။