အရေအတွက်များသောဥပဒေ- အဓိပ္ပါယ် + ဥပမာများ
နမူနာတစ်ခု၏ အရွယ်အစား တိုးလာသည်နှင့်အမျှ နမူနာဆိုလိုရင်းသည် မျှော်မှန်းတန်ဖိုးနှင့် နီးကပ်လာသည်ကို ကိန်းဂဏန်းကြီးများ၏ ဥပဒေက ဖော်ပြထားသည်။
အခြေခံအကျဆုံး ဥပမာမှာ အကြွေစေ့လှန်ခြင်း ဖြစ်သည်။ အကြွေစေ့ကိုလှန်လိုက်တိုင်း၊ ခေါင်းပေါ်တက်လာနိုင်ခြေက 1/2 ဖြစ်ပါတယ်။ ထို့ကြောင့် အကန့်အသတ်မရှိ လွှင့်ပစ်သည့် အရေအတွက်တွင် ပေါ်လာမည့် ဦးခေါင်းများ၏ မျှော်မှန်း အချိုးအစားမှာ 1/2 သို့မဟုတ် 0.5 ဖြစ်သည်။
သို့သော်၊ ကျွန်ုပ်တို့သည် အကြွေစေ့ကို ၁၀ ကြိမ်လှန်ပါက၊ ၎င်းသည် ခေါင်း ၃ ကြိမ်သာ ကျသည်ကို တွေ့ရှိနိုင်သည်။ 10 flips သည် သေးငယ်သောနမူနာအရွယ်အစားဖြစ်သောကြောင့် ဦးခေါင်းအချိုးအစား 0.5 နီးပါးရှိမည်ဟု အာမခံချက်မရှိပါ။
အကြွေစေ့ကို နောက်ထပ် 10 ကြိမ် ဆက်လှန်ရင်၊ အကြွေစေ့ 20 မှာ စုစုပေါင်း 9 ကြိမ် ခေါင်းပေါ်ကျတာကို တွေ့နိုင်ပါတယ်။ နောက် 10 ကြိမ် ထပ်ပစ်ရင် 30 မှာ 22 ကြိမ် ခေါင်းပေါ်ရောက်သွားတာကို တွေ့နိုင်ပါတယ်။
ကျွန်ုပ်တို့သည် အကြွေစေ့ကိုလှန်လိုက်သည်နှင့် ခေါင်းပေါ်တက်လာသည့်အကြိမ်အချိုးသည် မျှော်မှန်းထားသောအချိုးအစား 0.5 သို့ ရောက်ရှိလာမည်ဖြစ်သည်။
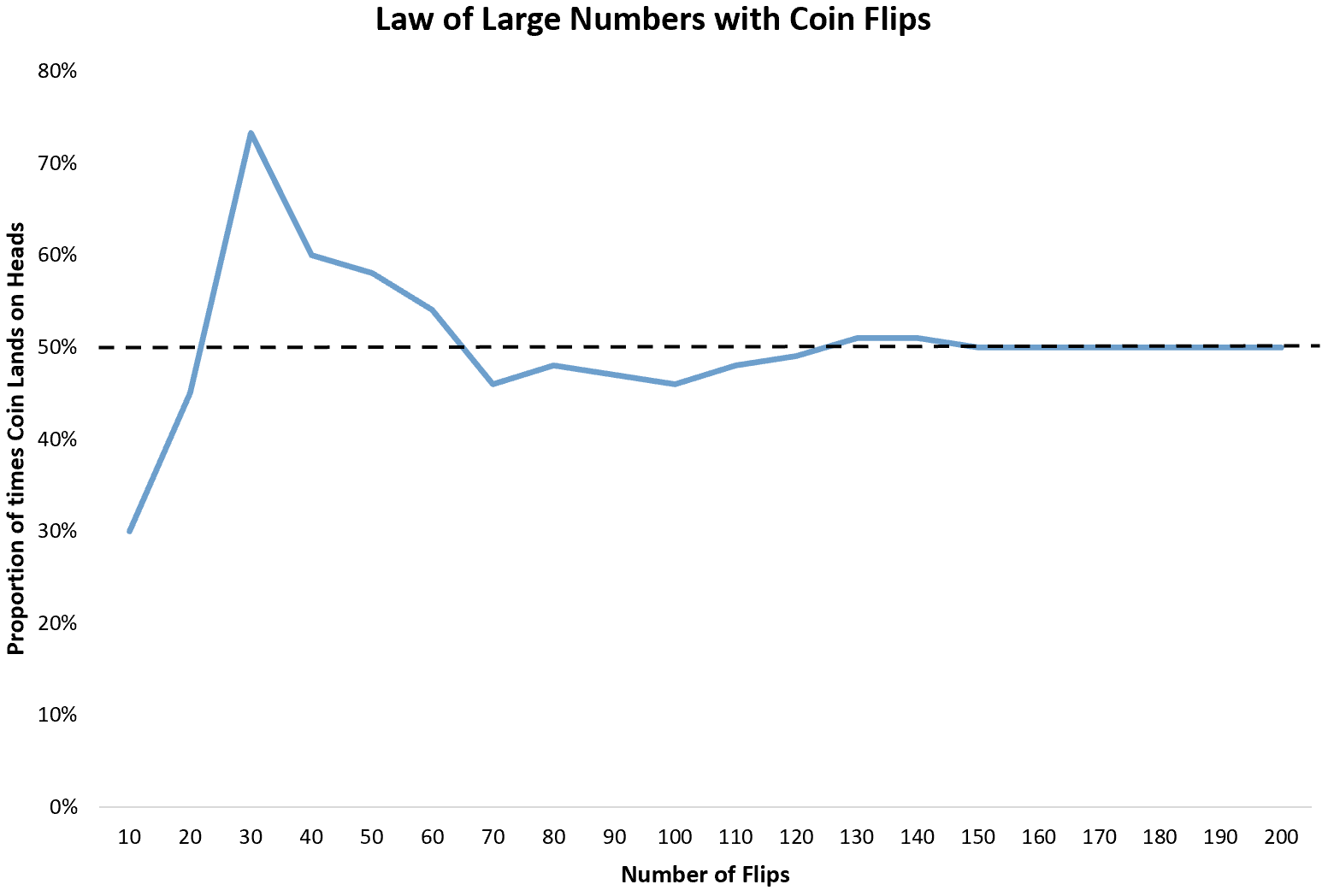
များပြားလှသော ဥပဒေ၏ ရိုးရှင်းသော စိတ်ကူးကို လက်တွေ့ဘဝတွင် လုပ်ငန်းအမျိုးအစားများစွာနှင့် စက်မှုလုပ်ငန်းများက အသုံးချသည်။
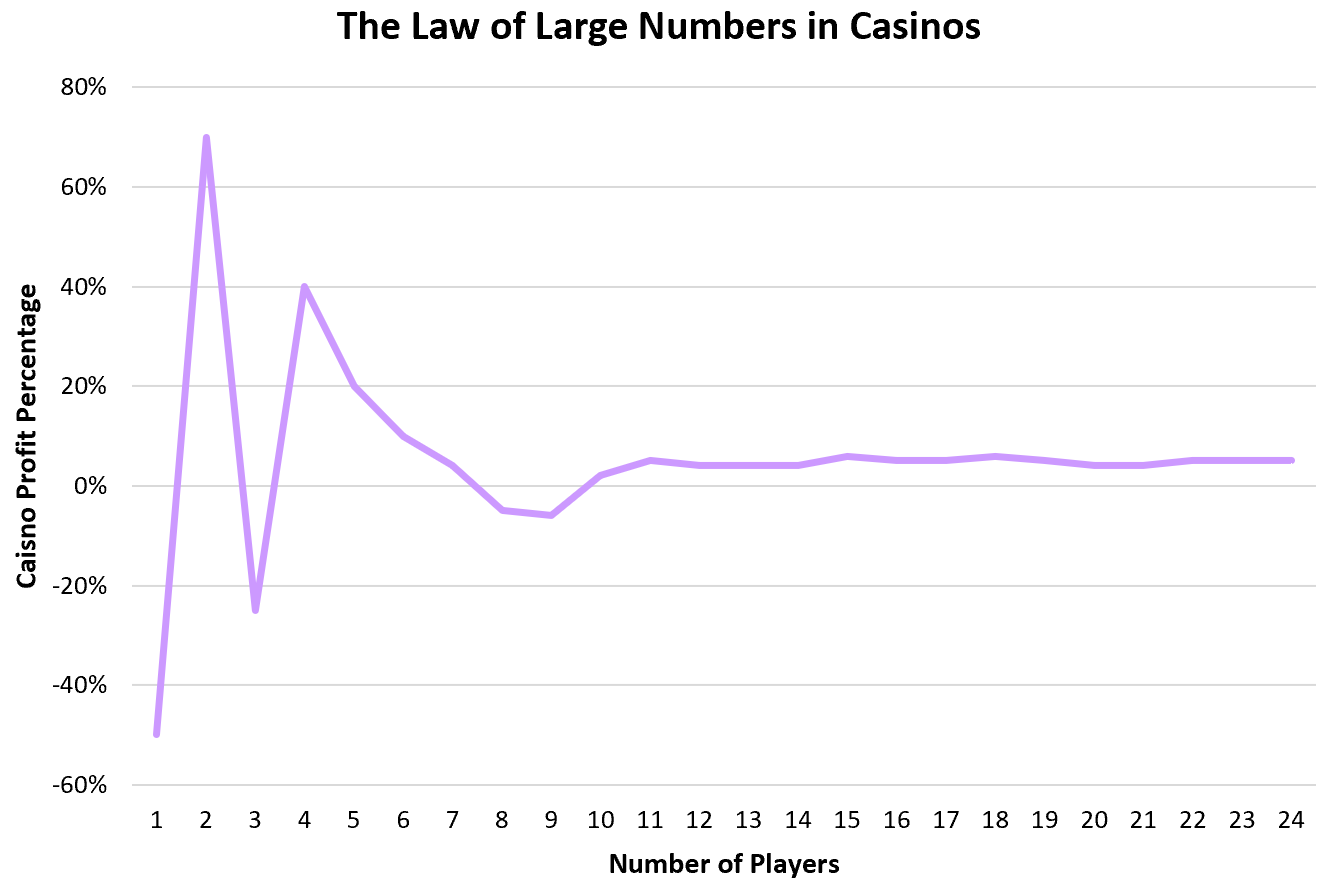
ကာစီနိုလောင်းကစားရုံများတွင်အများအပြားဥပဒေ
ကာစီနိုများသည် အမြတ်အစွန်းများကို ယုံကြည်စိတ်ချစွာ ထုတ်ပေးရန်အတွက် အများအပြား၏ ဥပဒေအပေါ် အားကိုးသည်။ ဂိမ်းအများစုအတွက်၊ ကာစီနိုသည် အချိန်၏ 51-55% ခန့် အနိုင်ရသည်။ ဆိုလိုသည်မှာ လူတစ်ဦးချင်းစီသည် ကံကောင်းပြီး သင့်တင့်သောပမာဏကို ခဏခဏအနိုင်ရနိုင်သော်လည်း တစ်ဦးချင်းကစားသမားထောင်ပေါင်းများစွာထဲမှ ကာစီနိုသည် မျှော်လင့်ထားသည့်အချိန်၏ 51-55% ကို အနိုင်ရမည်ဖြစ်သည်။
ဥပမာအားဖြင့်၊ Jessica သည် ကာစီနိုတွင် ဂိမ်းအနည်းငယ်ကစားနိုင်ပြီး $50 ရရှိနိုင်သည်။
Mike သည် ဂိမ်းအနည်းငယ်ကစားနိုင်ပြီး ဒေါ်လာ 70 ဆုံးရှုံးနိုင်သည်။
John သည် ဂိမ်းအနည်းငယ်ကစားနိုင်ပြီး $25 ဖြင့်အနိုင်ရရှိနိုင်သည်။
Susan သည် ဂိမ်းအနည်းငယ်ကစားနိုင်ပြီး $40 ဆုံးရှုံးနိုင်သည်။
အချို့သောကစားသမားများသည် ငွေအနိုင်ရပြီး အခြားသူများမှာ ငွေဆုံးရှုံးမည်ဖြစ်သော်လည်း ဂိမ်းများကို ဒီဇိုင်းရေးဆွဲထားခြင်းကြောင့် ကာစီနိုများသည် ထောင်နှင့်ချီသောတစ်ဦးချင်းစီမှ အနိုင်ရမည်ဟု စိတ်ချနိုင်ပါသည်။
အာမခံဥပဒေတွင် အများအပြားရှိသည်။
အာမခံကုမ္ပဏီများသည်လည်း အမြတ်အစွန်းများစွာရရှိရန် ဥပဒေအပေါ် အားကိုးကြသည်။
အခြေခံအယူအဆမှာ ထောင်နှင့်ချီသော အာမခံကုမ္ပဏီများသည် လစဉ် ပရီမီယံကြေးပေးဆောင်သူများကို အာမခံပေးနိုင်ပြီး ၎င်းတို့အာမခံထားသူများ၏ ရာခိုင်နှုန်းအနည်းငယ်သာ မထင်မှတ်ထားသော အသုံးစရိတ်များအတွက် အမှန်တကယ်လိုအပ်မည့် အာမခံကို အသုံးပြုရန် လိုအပ်ပါသည်။
ဥပမာအားဖြင့် လူ ၁,၀၀၀ သည် အာမခံကုမ္ပဏီတစ်ခုအတွက် အမြတ်ငွေ ဒေါ်လာ ၁,၀၀၀,၀၀၀ ကို တစ်နှစ်လျှင် အာမခံအတွက် ဒေါ်လာ ၁,၀၀၀ ပေးဆောင်နိုင်သည်။
သို့သော်လည်း လူ 90 သည် မတော်တဆမှုအမျိုးမျိုးနှင့် သက်ဆိုင်သည့် မမျှော်လင့်ထားသော အသုံးစရိတ်များကို ကာမိစေရန် အာမခံကုမ္ပဏီထံမှ ဒေါ်လာ 10,000 ရရှိရန် လိုအပ်ပြီး အာမခံကုမ္ပဏီအတွက် 900,000 ဒေါ်လာ ဆုံးရှုံးသွားမည်ဖြစ်သည်။
နောက်ဆုံးတွင် အာမခံကုမ္ပဏီသည် အမြတ်ငွေ $1,000,000 မှ $900,000 = $100,000 ရရှိသည်။
ဆိုလိုသည်မှာ အာမခံကုမ္ပဏီသည် ပျမ်းမျှအားဖြင့် လူထောင်ပေါင်းများစွာတွင် မျှမျှတတ ကြိုတင်မှန်းဆနိုင်သော အမြတ်အစွန်းရရှိရန် မျှော်လင့်နိုင်သည်ဟု ဆိုလိုသည်။
အာမခံကုမ္ပဏီသည် လူအများအပြားကို အာမခံထားသောကြောင့် ဤစီးပွားရေးပုံစံသည် အလုပ်ဖြစ်သည်ကို သတိပြုပါ။ လူ 10 ဦးသာ အာမခံထားမည်ဆိုပါက မထင်မှတ်ထားသော ကုန်ကျစရိတ်ကြီးကြီးမားမားကြောင့် လုပ်ငန်းကို ပျက်ပြားစေနိုင်သောကြောင့် အလွန်အန္တရာယ်များပါသည်။
ထို့ကြောင့် အာမခံကုမ္ပဏီများသည် ၎င်းတို့၏အမြတ်အစွန်းများကို ကြိုတင်ခန့်မှန်းနိုင်သော နည်းလမ်းဖြင့် အရေအတွက်များစွာ၏ ဥပဒေအပေါ် အားကိုးကြသည်။
ပြန်လည်ပြည့်ဖြိုးမြဲစွမ်းအင်များတွင် အရေအတွက်များသော ဥပဒေ
ပြန်လည်ပြည့်ဖြိုးမြဲစွမ်းအင်ကုမ္ပဏီများမှလည်း အရေအတွက်များသော ဥပဒေကိုလည်း အသုံးပြုပါသည်။
အခြေခံအယူအဆမှာ လေအားတာဘိုင်များနှင့် ဆိုလာပြားများသည် လုပ်ငန်း၏ အစိတ်အပိုင်းအသီးသီးတွင် လျှပ်စစ်ဓာတ်အားထုတ်လုပ်ရန် ဂျင်နရေတာများကို ပါဝါပေးနိုင်သည်။ သို့သော် အပြင်တွင်လေ သို့မဟုတ် နေရောင်မရှိသောကြောင့် လေအားတာဘိုင်များနှင့် ဆိုလာပြားများသည် လျှပ်စစ်မီးစက်များအတွက် ယုံကြည်စိတ်ချရသောစွမ်းအင်ကို အမြဲမထုတ်လုပ်နိုင်ဟု ဆိုလိုသည်။
ပြန်လည်ပြည့်ဖြိုးမြဲစွမ်းအင်ကုမ္ပဏီများသည် ဤပြဿနာကို ပြေလည်အောင်ဖြေရှင်းနည်းမှာ ထောင်သောင်းချီသော လေတာဘိုင်များ သို့မဟုတ် ဆိုလာပြားများကို မဟာဓာတ်အားလိုင်းတစ်ခုတည်းသို့ ချိတ်ဆက်ရန်ဖြစ်ပြီး အဆိုပါစွမ်းအင်ရင်းမြစ်များသည် ယုံကြည်စိတ်ချရသော စွမ်းအင်ပမာဏကို ထုတ်ပေးနိုင်စေရန် အလားအလာများစွာရှိနေသည်။ ကွန်ရက်အတွက် စွမ်းအင်။
အင်ဂျင်နီယာများသည် ပျမ်းမျှ လေအားတာဘိုင် သို့မဟုတ် ဆိုလာပြား သောင်းနှင့်ချီ၍ မျှော်မှန်းထားသောကြောင့် စွမ်းအင်မည်မျှ ထုတ်လုပ်မည်ကို ခန့်မှန်းရန်လည်း ပိုမိုလွယ်ကူပါသည်။
ဤဖြစ်စဉ်နှင့်ပတ်သက်၍ အသေးစိတ်ရှင်းလင်းချက်ကို ဤ Scientific American ဆောင်းပါးတွင် တွေ့နိုင်ပါသည်။