ကျောင်းသား၏ t ဖြန့်ဝေ

အားဖြင့် ဩဂုတ် 4, 2023 ဖြစ်နိုင်ခြေ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် Student t ဖြန့်ဝေမှုသည် အဘယ်အရာနှင့် ၎င်းကိုအသုံးပြုကြောင်း ရှင်းပြထားသည်။ ထို့အပြင်၊ Student’s t distribution ၏ ဂရပ်ကို ပြသထားပြီး ဤဖြစ်နိုင်ခြေ ဖြန့်ဖြူးမှုအမျိုးအစား၏ လက္ခဏာများကား အဘယ်နည်း။

ကျောင်းသား၏ဖြန့်ဝေမှုကား အဘယ်နည်း။

Student’s t distribution သည် စာရင်းဇယားများတွင် အသုံးများသော ဖြစ်နိုင်ခြေဖြန့်ဝေမှုတစ်ခုဖြစ်သည်။ အထူးသဖြင့်၊ ကျောင်းသား၏ t ဖြန့်ဝေမှုကို နမူနာနှစ်ခု၏နည်းလမ်းများကြား ခြားနားချက်အား ဆုံးဖြတ်ရန်နှင့် ယုံကြည်မှုကြားကာလများသတ်မှတ်ရန် ကျောင်းသား၏ t စမ်းသပ်မှုတွင် အသုံးပြုသည်။

ကျောင်းသား၏ t ဖြန့်ဖြူးမှုကို စာရင်းအင်းပညာရှင် William Sealy Gosset မှ ၁၉၀၈ ခုနှစ်တွင် ကလောင်အမည် “ ကျောင်းသား” အောက်တွင် တီထွင်ခဲ့သည်။

ကျောင်းသား၏ t ဖြန့်ဝေမှုကို လေ့လာသုံးသပ်မှုစုစုပေါင်းမှ တစ်ယူနစ်ကို နုတ်ခြင်းဖြင့် ရရှိသော လွတ်လပ်မှုဒီဂရီအရေအတွက်ဖြင့် သတ်မှတ်သည်။ ထို့ကြောင့်၊ ကျောင်းသားတစ်ဦး၏ t ဖြန့်ဝေမှု၏ လွတ်လပ်မှုဒီဂရီကို ဆုံးဖြတ်ရန် ဖော်မြူလာမှာ ν=n-1 ဖြစ်သည်။

\begin{array}{c}\nu=n-1\\[2ex]X\sim t_\nu\end{array}

ကျောင်းသား၏ t ဖြန့်ဝေဂရပ်

Student’s t distribution ၏ အဓိပ္ပါယ်ကို ယခုကျွန်ုပ်တို့သိပြီ၊ ၎င်း၏ဂရပ်သည် အဘယ်အရာဖြစ်သည်ကို ကြည့်ကြပါစို့။ ထို့ကြောင့်၊ အောက်တွင် လွတ်လပ်မှုဒီဂရီအမျိုးမျိုးဖြင့် Student’s t distributions ၏ နမူနာအများအပြားကို ကွက်ကွက်ကွင်းကွင်းမြင်နိုင်သည်။

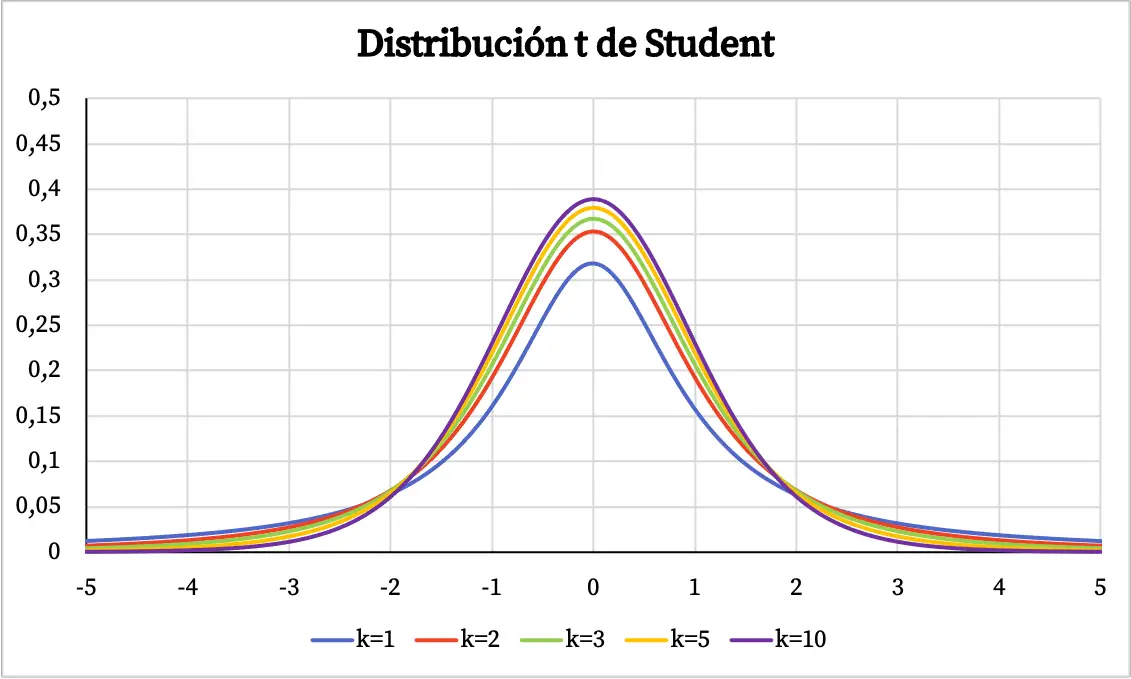
ကျောင်းသား၏ t ဖြန့်ဝေဂရပ်

Student’s t distribution ၏ ဂရပ်မှ၊ အောက်ပါ ဂုဏ်သတ္တိများကို နုတ်ယူနိုင်သည်-

  • Student t ဖြန့်ဝေမှုသည် 0 တွင် အချိုးကျဗဟိုပြုထားပြီး ခေါင်းလောင်းပုံသဏ္ဍာန်ရှိသည်။
  • ကျောင်းသား၏ t ဖြန့်ဝေမှုသည် ပုံမှန်ဖြန့်ဝေမှုထက် ပိုမိုပြန့်ကျဲသည်၊ ဆိုလိုသည်မှာ ကျောင်းသား၏ t ဖြန့်ဝေမှုမျဉ်းကွေးသည် ပိုကျယ်သည်။
  • ကျောင်းသား၏ t ဖြန့်ဝေမှုတွင် လွတ်လပ်မှုဒီဂရီ များလေလေ၊ ၎င်း၏ ကွဲလွဲမှု နည်းပါးလေဖြစ်သည်။

အထက်ဖော်ပြပါ ဂရပ်တွင်၊ ကျောင်းသား၏ t ဖြန့်ဝေမှု၏ သိပ်သည်းဆလုပ်ဆောင်ချက်သည် ၎င်း၏ လွတ်လပ်မှုဒီဂရီများနှင့် ဆန့်ကျင်ဘက်ဖြစ်သည်။ သို့သော်၊ ကျောင်းသား၏ t ဖြန့်ဝေမှု၏ တိုးပွားလာနိုင်သည့် ဖြစ်နိုင်ခြေလုပ်ဆောင်ချက်ကို အောက်တွင် သင်ကြည့်ရှုနိုင်သည်-

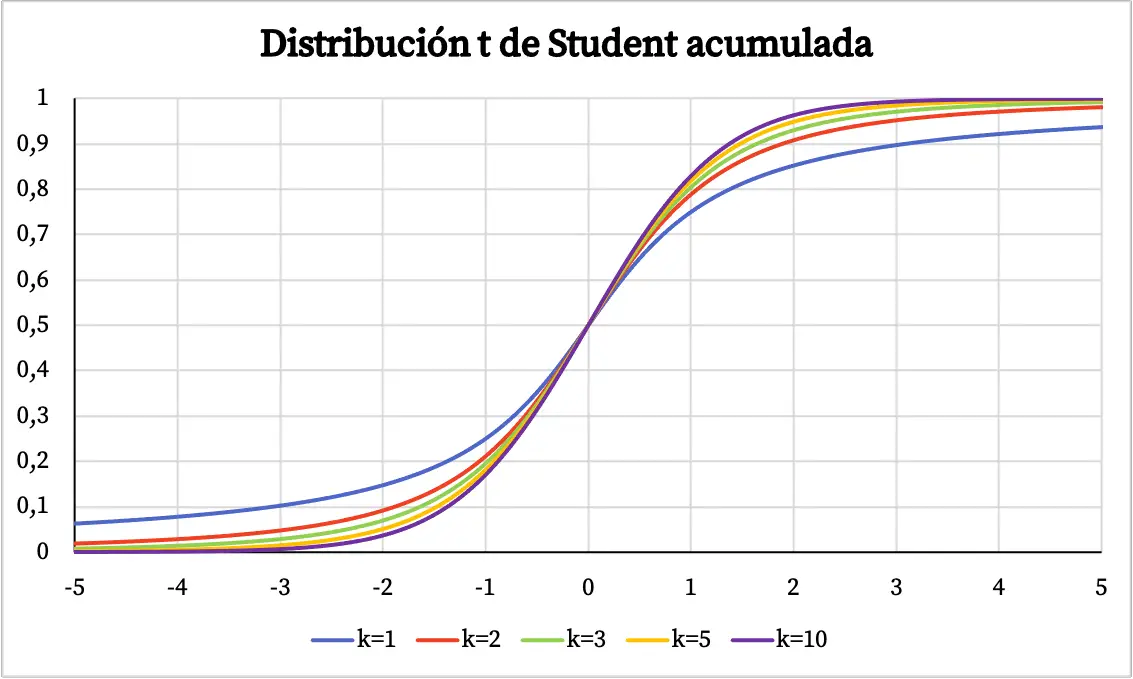
Student's cumulative t ဖြန့်ချီရေးကွက်

ကျောင်းသား၏ t ဖြန့်ဖြူးခြင်း၏လက္ခဏာများ

Student’s t distribution ၏ အရေးကြီးဆုံးလက္ခဏာများကို အောက်တွင်ဖော်ပြထားသည်။

  • Student t ဖြန့်ဖြူးမှု၏ဒိုမိန်းတွင် ကိန်းဂဏန်းအစစ်အမှန်များ ပါဝင်သည်။

x\in (-\infty, +\infty)

  • လွတ်လပ်မှုအတိုင်းအတာတစ်ခုထက်ပိုသော ကျောင်းသား၏ t ဖြန့်ဝေမှုအတွက်၊ ဖြန့်ဖြူးမှု၏ပျမ်းမျှသည် 0 နှင့် ညီမျှသည်။

\begin{array}{c}X\sim t_\nu\\[2ex] E[X]=0 \qquad \text{para }\nu>1\end{array} ” title=” Rendered by QuickLaTeX.com” height=” 55″ width=” 190″ style=” vertical-align: 0px;” ></p> </p> <ul> <li> ကျောင်းသား၏ t ဖြန့်ဝေမှု၏ကွဲလွဲမှုကို အောက်ပါအသုံးအနှုန်းဖြင့် တွက်ချက်နိုင်သည်-</li> </ul> <p class=\begin{array}{c}X\sim t_\nu\\[2ex] Var(X)=\cfrac{\nu}{\nu-2} \qquad \text{para }\nu>2\end{array} ” title=” Rendered by QuickLaTeX.com” height=” 75″ width=” 245″ style=” vertical-align: 0px;” ></p> </p> <ul> <li> လွတ်လပ်မှုဒီဂရီ အရေအတွက် မခွဲခြားဘဲ ကျောင်းသား၏ t ဖြန့်ဖြူးမှု၏ ပျမ်းမျှနှင့် မုဒ်သည် အမြဲတမ်း 0 ဖြစ်သည်။</li> </ul> <p class=\begin{array}{c}Me=0\\[2ex]Mo=0\end{array}

  • Student t ဖြန့်ဝေမှု၏ သိပ်သည်းဆကို အောက်ပါဖော်မြူလာဖြင့် သတ်မှတ်သည်-

\displaystyle P[X=x]=\frac{\Gamma((\nu+1)/2)} {\sqrt{\nu\pi}\,\Gamma(\nu/2)} (1+x^2/\nu)^{-(\nu+1)/2}

  • ကျောင်းသား၏ t ဖြန့်ဝေမှု၏ တိုးပွားဖြစ်နိုင်ခြေဖြန့်ဝေမှုလုပ်ဆောင်ချက်ကို အောက်ပါဖော်မြူလာဖြင့် သတ်မှတ်သည်-

\displaystyle P[X\leq x]=\frac{1}{2} + x \Gamma \left( \frac{\nu+1}{2} \right) \cdot\frac{\,_2F_1 \left ( \frac{1}{2},\frac{\nu+1}{2};\frac{3}{2};-\frac{x^2}{\nu} \right)}{\sqrt{\pi\nu}\,\Gamma \left(\frac{\nu}{2}\right)}

  • 3 ထက်ကြီးသော လွတ်လပ်မှုဒီဂရီဖြင့် ကျောင်းသား၏ t ဖြန့်ဝေမှုအတွက်၊ အချိုးမညီသောကိန်းဂဏန်းသည် သုညဖြစ်ပြီး ၎င်းသည် အချိုးညီသောဖြန့်ဝေမှုဖြစ်သောကြောင့် ဖြစ်သည်။

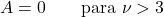
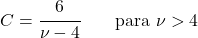\displaystyle A=0\qquad \text{para }\nu>3″ title=” Rendered by QuickLaTeX.com” height=” 17″ width=” 164″ style=” vertical-align: -4px;” ></p> </p> <ul> <li> ကျောင်းသား၏ t ဖြန့်ဝေမှု၏ လွတ်လပ်မှုဒီဂရီသည် လေးခုထက် ကြီးပါက၊ လွတ်လပ်မှုဒီဂရီ အနှုတ် လေးခုဖြင့် ခြောက်ခုကို ပိုင်းခြားခြင်းဖြင့် kurtosis ကို တွက်ချက်နိုင်သည်။ </li> </ul> <p class=\displaystyle C=\cfrac{6}{\nu-4}\qquad \text{para }\nu>4″ title=” Rendered by QuickLaTeX.com” height=” 38″ width=” 198″ style=” vertical-align: -12px;” ></p> </p> <h2 class= Student’s t distribution ၏ အသုံးချမှုများ

Student’s t distribution သည် စာရင်းဇယားများတွင် အသုံးများသော ဖြစ်နိုင်ခြေဖြန့်ဝေမှုတစ်ခုဖြစ်သည်။ အမှန်မှာ၊ အယူအဆများနှင့် ယုံကြည်မှုကြားကာလများကို စမ်းသပ်ရန်အတွက် အသုံးပြုသည့် Student’s t-test ပင် ရှိပါသည်။

ထို့ကြောင့် ကျောင်းသား၏ t ဖြန့်ဖြူးမှုသည် ကျွန်ုပ်တို့အား နမူနာနှစ်ခု၏နည်းလမ်းများအကြား ခြားနားချက်ကို ခွဲခြမ်းစိတ်ဖြာနိုင်စေပြီး၊ နမူနာနှစ်ခုသည် သိသိသာသာကွာခြားမှုရှိမရှိ ဆုံးဖြတ်ရန် ၎င်းကိုအသုံးပြုသည်။ အလားတူ၊ ကျောင်းသား၏ t test ကို linear regression analysis မှရရှိသောမျဉ်းသည် slope ရှိ၊ မရှိ သိရှိရန်အသုံးပြုသည်။

အတိုချုပ်အားဖြင့်၊ Student’s t distribution ၏ applications များသည် သီအိုရီအရ ပုံမှန်ဖြန့်ဝေမှုအတိုင်း လိုက်နာသော data set များ၏ ခွဲခြမ်းစိတ်ဖြာမှုအပေါ် အားကိုးသော်လည်း ဤဖြန့်ဖြူးမှုအမျိုးအစားကို အသုံးပြုရန် စုစုပေါင်း လေ့လာတွေ့ရှိချက်အရေအတွက်မှာ နည်းပါးလွန်းပါသည်။

စာရေးသူအကြောင်း

Benjamin Anderson
Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။

မှတ်ချက်တစ်ခုထည့်ပါ။

သင့် email လိပ်စာကို ဖော်ပြမည် မဟုတ်ပါ။ လိုအပ်သော ကွက်လပ်များကို * ဖြင့်မှတ်သားထားသည်