ကျောင်းသား၏ t-test
ဤဆောင်းပါးတွင် Student t test သည် အဘယ်အရာနှင့် ၎င်းကို စာရင်းအင်းများတွင် အသုံးပြုကြောင်း ရှင်းပြထားသည်။ ထို့ကြောင့်၊ ကျောင်းသား၏ t စာမေးပွဲကို မည်သို့ဆောင်ရွက်သည်၊ ကျောင်းသား၏ t စာမေးပွဲ အမျိုးအစားများ နှင့် တစ်ခုစီအတွက် ဖော်မြူလာ မည်သည်တို့ကို ရှာဖွေတွေ့ရှိနိုင်မည်ဖြစ်သည်။
ကျောင်းသားရဲ့ t-test ဆိုတာဘာလဲ။
ကျောင်းသား၏ t-test ကို T-test သို့မဟုတ် ရိုးရိုး t-test ဟုလည်း ခေါ်သည် ၊ စာမေးပွဲ ကိန်းဂဏန်းသည် ကျောင်းသား၏ t-ဖြန့်ဝေမှုကို လိုက်နာသည့် စာရင်းအင်းဆိုင်ရာ စာမေးပွဲ ဖြစ်သည်။ ထို့ကြောင့်၊ စာရင်းဇယားများတွင် ကျောင်းသား၏ t-test ကို hypothesis test တစ်ခု၏ null hypothesis ကို ငြင်းပယ်ရန် သို့မဟုတ် လက်ခံရန် အသုံးပြုသည်။
အတိအကျအားဖြင့်၊ ကျောင်းသား၏ t-test ကို လေ့လာသည့်လူဦးရေသည် ပုံမှန်ဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်သည့် သီအိုရီစစ်ဆေးမှု တွင် အသုံးပြုသော်လည်း နမူနာအရွယ်အစားမှာ လူဦးရေကွဲလွဲမှုကို သိရှိရန် သေးငယ်လွန်းပါသည်။
အတိုချုပ်အားဖြင့်၊ Student’s t-test ကို အချို့သော ယူဆချက်စမ်းသပ်မှုများ၏ လေ့လာမှုဆိုင်ရာ ယူဆချက်အား ငြင်းပယ်ရန် သို့မဟုတ် လက်ခံရန် အသုံးပြုသည်။ ဥပမာအားဖြင့်၊ ကျောင်းသား၏ t-test ကို နမူနာတစ်ခုအတွက်၊ အမှီအခိုကင်းသောနမူနာများအတွက် သို့မဟုတ် ဆက်စပ်နမူနာများအတွက် ယူဆချက်များအား စမ်းသပ်ရန် အသုံးပြုပါသည်။ ထို့နောက် ကျောင်းသား၏ t စာမေးပွဲကို အမှုတစ်ခုစီတွင် မည်သို့တွက်ချက်သည်ကို ကြည့်ပါမည်။
ကျောင်းသား၏ t-test အမျိုးအစားများ
Student’s t tests မှာ သုံးမျိုးရှိပါတယ်။
- ကျောင်းသားတစ်ဦးတည်း၏ t-test-နမူနာ ဆိုလိုချက်၏တန်ဖိုးနှင့်ပတ်သက်သည့် ယူဆချက်အား စမ်းသပ်ရန်အတွက် အသုံးပြုသည်။
- အမှီအခိုကင်းသောနမူနာနှစ်ခုအတွက် ကျောင်းသား၏ t စမ်းသပ်မှု – ၎င်းသည် သီးခြားလွတ်လပ်သောနမူနာနှစ်ခု၏ ဆိုလိုရင်းများကြား ခြားနားချက်အပေါ် ယူဆချက်အား စမ်းသပ်နိုင်စေပါသည်။
- တွဲထားသောနမူနာနှစ်ခု (သို့မဟုတ် ဆက်စပ်နမူနာများ) အတွက် ကျောင်းသား၏ t-test ကို – နှစ်ကြိမ်စမ်းသပ်ထားသောနမူနာတစ်ခု၏ ဆိုလိုရင်းနှင့်ပတ်သက်သော သီအိုရီကို စုံစမ်းစစ်ဆေးရန် အသုံးပြုသည်။
Student’s t test နမူနာ
နမူနာဆိုလိုချက်အတွက် အယူအဆစမ်းသပ်မှုများသည် null hypothesis နှင့် test ၏ အခြား hypothesis တို့သည် လူဦးရေ၏တန်ဖိုးကိုဆိုလိုခြင်းနှင့်ပတ်သက်၍ တစ်စုံတစ်ရာဖော်ပြသည့်အရာများဖြစ်သည်။
နမူနာ ကျောင်းသား t စာမေးပွဲအတွက် ဖော်မြူလာမှာ အောက်ပါအတိုင်း ဖြစ်ပါသည်။

ရွှေ-
-

ကျောင်းသား၏ t ဖြန့်ဝေမှုဖြင့် သတ်မှတ်ထားသော ပျမ်းမျှအတွက် သီအိုရီစစ်ဆေးမှု ကိန်းဂဏန်းဖြစ်သည်။
-

နမူနာဆိုလိုသည်။
-

hypothesis test တွင် တင်ပြထားသော ပျမ်းမျှတန်ဖိုးဖြစ်သည်။
-

နမူနာစံသွေဖည်သည်။
-

နမူနာအရွယ်အစားဖြစ်သည်။
Student’s t test ၏တန်ဖိုးကို တွက်ချက်ပြီးသည်နှင့်၊ အရေးကြီးသောတန်ဖိုးဖြင့် ကိန်းဂဏန်းစမ်းသပ်မှုရလဒ်သည် null hypothesis ကို ငြင်းပယ်ရန် သို့မဟုတ် မဟုတ်ဘူးဟု အဓိပ္ပာယ်ပြန်ဆိုရပါမည်။
- ပျမ်းမျှအတွက် သီအိုရီစစ်ဆေးမှုသည် နှစ်ဖက်သဘောတူပါက၊ ကျောင်းသား၏ t စမ်းသပ်မှု၏ ပကတိတန်ဖိုးသည် အရေးကြီးသောတန်ဖိုး t α/2|n-1 ထက် ကြီးနေပါက null hypothesis ကို ပယ်ချပါသည်။
- ပျမ်းမျှအတွက် သီအိုရီစစ်ဆေးမှုသည် ညာဘက်အမြီးနှင့် ကိုက်ညီပါက ကျောင်းသား၏ t-test တန်ဖိုးသည် အရေးကြီးသောတန်ဖိုး t α|n-1 ထက် ကြီးနေပါက null hypothesis ကို ပယ်ချပါသည်။
- ပျမ်းမျှတွက်ဆချက်စစ်ဆေးမှုသည် ဘယ်အမြီးနှင့်ကိုက်ညီပါက ကျောင်းသား၏ t-test တန်ဖိုးသည် အရေးကြီးသောတန်ဖိုး -t α|n-1 ထက်နည်းပါက null hypothesis ကို ပယ်ချပါသည်။
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-31fb206b75a47181c7c673f54ba28ee8_l3.png)
အရေးကြီးသော စမ်းသပ်မှုတန်ဖိုးများကို ကျောင်းသား၏ ဖြန့်ချီရေးဇယားမှ ရယူကြောင်း သတိပြုပါ။
လွတ်လပ်သောနမူနာများအတွက် ကျောင်းသား၏ t စာမေးပွဲ
အမှီအခိုကင်းသောနမူနာများအတွက် ကျောင်းသား၏ t-test ကို လူဦးရေနှစ်ခု၏ဆိုလိုရင်းကို ငြင်းဆိုခြင်း သို့မဟုတ် လက်ခံရန်အသုံးပြုသည်၊ ဥပမာ လူဦးရေနှစ်ခု၏ဆိုလိုသည်မှာ ကွဲပြားသည် သို့မဟုတ် လူဦးရေ၏ပျမ်းမျှ A သည် ပျမ်းမျှထက်ပိုများသည်ဟု ယူဆချက်ကို ငြင်းပယ်ရန် သို့မဟုတ် လက်ခံရန်အသုံးပြုသည်။ . လူဦးရေ B
သို့သော်လည်း ဤကိစ္စတွင်၊ ကျောင်းသား၏ t-test ဖော်မြူလာသည် လူဦးရေကွဲလွဲမှု တူညီသည် သို့မဟုတ် မဟု ယူဆနိုင်သည်အပေါ် မူတည်၍ ကွဲပြားသည်။ ပြီးရင် ဖြစ်နိုင်တဲ့ ကိစ္စနှစ်ခုကို ကြည့်မယ်။
အမည်မသိနှင့် တန်းတူသွေဖီသည်။
လူဦးရေကွဲလွဲမှုကို မသိသော်လည်း တန်းတူဟုယူဆသောအခါ သီးခြားနမူနာများအတွက် Student t စာမေးပွဲကို တွက်ချက်ရန် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်-

ရွှေ-
-

ကျောင်းသားတစ်ဦး၏ t ဖြန့်ဝေမှုနောက်တွင် လွတ်မြောက်မှု n 1 + n 2 -2 ဒီဂရီဖြင့် ကျောင်းသား၏ t ဖြန့်ဝေမှုနောက်တွင် အမည်မသိကွဲလွဲမှုများရှိသည့် နည်းလမ်းများ၏ ခြားနားချက်အတွက် သီအိုရီစမ်းသပ်ကိန်းဂဏန်းဖြစ်သည်။
-

လူဦးရေရဲ့ ပျမ်းမျှ ကိန်းဂဏန်းက ၁။
-

လူဦးရေ ပျမ်းမျှ ၂။
-

နမူနာ 1 ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
-

နမူနာ 2 ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
-

စံသွေဖည်မှု ပေါင်းစည်းသည်။
-

နမူနာအရွယ်အစား 1 ဖြစ်ပါတယ်။
-

နမူနာအရွယ်အစား 2 ဖြစ်ပါတယ်။
နမူနာနှစ်ခု၏ ပေါင်းစပ်စံသွေဖည်မှုကို အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်သည်-

အမည်မသိနှင့် မတူညီသော ကွဲပြားမှုများ
လူဦးရေကွဲလွဲမှုကို မသိရသည့်အပြင် ကွဲပြားသည်ဟု ယူဆသောအခါ၊ သီးခြားနမူနာများအတွက် Student’s t test တွက်ချက်ခြင်းဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်-

ရွှေ-
-

ကျောင်းသား၏ t ဖြန့်ဝေမှုကို လိုက်နာသော အမည်မသိကွဲလွဲမှုများနှင့် အဓိပ္ပါယ်ကွဲပြားမှုအတွက် သီအိုရီစမ်းသပ်မှု ကိန်းဂဏန်းများဖြစ်သည်။
-

လူဦးရေရဲ့ ပျမ်းမျှ ကိန်းဂဏန်းက ၁။
-

လူဦးရေ ပျမ်းမျှ ၂။
-

နမူနာ 1 ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
-

နမူနာ 2 ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
-

လူဦးရေ ၁ ၏ စံသွေဖည်သည်။
-

လူဦးရေ ၂ ၏ စံသွေဖည်သည်။
-

နမူနာအရွယ်အစား 1 ဖြစ်ပါတယ်။
-

နမူနာအရွယ်အစား 2 ဖြစ်ပါတယ်။
သို့ရာတွင်၊ ဤကိစ္စတွင်၊ ကျောင်းသား၏ t ဖြန့်ဖြူးမှု၏ လွတ်လပ်မှုဒီဂရီကို အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်သည်-

တွဲထားသော သို့မဟုတ် ဆက်စပ်နမူနာများအတွက် ကျောင်းသား၏ t စာမေးပွဲ
လေ့လာမှုနမူနာနှစ်ခုသည် တစ်ခုနှင့်တစ်ခု ဆက်စပ်နေသောအခါတွင် ဤစမ်းသပ်မှုကို အသုံးပြုသည်၊ ထို့ကြောင့် ၎င်းသည် အမှန်တကယ် နှစ်ကြိမ်ခွဲခြမ်းစိတ်ဖြာထားသော လူတစ်ဦးချင်းစီ၏ နမူနာတစ်ခုဖြစ်သည် ( မတူညီသောအခြေအနေများတွင် တစ်ကြိမ်စီ)။
ဥပမာအားဖြင့်၊ ဘာသာရပ်နှစ်ခုအတွက် ပျမ်းမျှ ကွာခြားချက်ရှိမရှိ သိနိုင်ရန် သင်္ချာနှင့် စာရင်းအင်းသင်တန်းတွင် ကျောင်းသားအဆင့်များကို ပိုင်းခြားစိတ်ဖြာနိုင်ပါသည်။ ဤအခြေအနေတွင်၊ ကျောင်းသားတစ်ဦးစီ၏ သင်္ချာအဆင့်သည် ထိုကျောင်းသား၏ ကိန်းဂဏန်းအဆင့်နှင့် ချိတ်ဆက်ထားသည်။
တွဲထားသော သို့မဟုတ် ဆက်စပ်နမူနာများအတွက် ကျောင်းသား၏ t-test ဖော်မြူလာ မှာ-
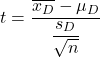
ရွှေ-
-

ကျောင်းသား၏ t ဖြန့်ဝေမှုဖြင့် သတ်မှတ်ထားသော တွဲထားသည့်နည်းလမ်းများအတွက် သီအိုရီစမ်းသပ်မှု ကိန်းဂဏန်းဖြစ်သည်။
-
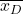
ဒေတာ ကွာခြားချက်ဖြင့် ဖွဲ့စည်းထားသော နမူနာ၏ ဆိုလိုရင်းဖြစ်သည်။
-
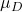
hypothesis test တွင် တင်ပြထားသော ပျမ်းမျှတန်ဖိုးဖြစ်သည်။
-
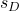
ဒေတာ ကွာခြားချက်ဖြင့် ဖွဲ့စည်းထားသော နမူနာ၏ စံသွေဖည်မှု ဖြစ်ပါသည်။
-

နမူနာအရွယ်အစားဖြစ်သည်။
ကျောင်းသား၏ t-test ယူဆချက်
Student’s t test ကိုလုပ်ဆောင်ရန်အတွက် အောက်ပါအခြေအနေများနှင့် ကိုက်ညီရပါမည်။
- Continuity – နမူနာဒေတာသည် စဉ်ဆက်မပြတ်ဖြစ်သည်။
- ကျပန်း – ဒေတာနမူနာများကို ကျပန်းရွေးချယ်ခဲ့သည်။
- တူညီခြင်း – ဒေတာနမူနာ၏ ကွဲလွဲမှုသည် တစ်သားတည်းဖြစ်နေသည်။
- Normality – ဒေတာနမူနာကို သတ်မှတ်သည့် ဖြန့်ဝေမှုသည် ခန့်မှန်းခြေအားဖြင့် ပုံမှန်ဖြစ်သည်။
ကျောင်းသား t စာမေးပွဲကို ဘယ်လိုဖြေရမလဲ
နောက်ဆုံးအနေဖြင့် အချုပ်အားဖြင့်၊ Student’s t test ပြုလုပ်ရန် လိုက်နာရမည့် အဆင့်များကို အသေးစိတ်ဖော်ပြထားသည်။
- သီအိုရီစမ်းသပ်ခြင်း၏ null နှင့် အခြားအခြားသော အယူအဆများကို သတ်မှတ်ပါ။
- အယူအဆစမ်းသပ်မှု၏ အရေးပါမှုအဆင့် (α) ကို သတ်မှတ်ပါ။
- ကျောင်းသား၏ t စာမေးပွဲ၏ ယူဆချက်များနှင့် ကိုက်ညီကြောင်း စစ်ဆေးပါ။
- သက်ဆိုင်ရာ ကျောင်းသား၏ t-test ဖော်မြူလာကို အသုံးချပြီး စာမေးပွဲစာရင်းအင်းကို တွက်ချက်ပါ။
- စာမေးပွဲ၏ အရေးပါသောတန်ဖိုးနှင့် နှိုင်းယှဉ်ခြင်းဖြင့် ကျောင်းသား၏ t စာမေးပွဲ၏ ရလဒ်ကို ဘာသာပြန်ပါ။