ကွဲလွဲမှုအတွက် ယူဆချက်စမ်းသပ်ခြင်း။

အားဖြင့် Benjamin Anderson ဩဂုတ် 3, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် ကွဲလွဲမှုများအတွက် သီအိုရီစမ်းသပ်ခြင်းဟူသည် မည်သည်ကို ရှင်းပြထားသည်။ ထို့ကြောင့်၊ ကွဲလွဲမှုယူဆချက်စမ်းသပ်ခြင်းအတွက် ဖော်မြူလာကို တွေ့ရမည်ဖြစ်ပြီး၊ ထို့အပြင် လေ့ကျင့်ခန်းတစ်ခုပြီးတစ်ခု အဆင့်ဆင့်ဖြေရှင်းထားသည်။

ကွဲလွဲမှုအတွက် သီအိုရီစမ်းသပ်ခြင်းဆိုသည်မှာ အဘယ်နည်း။

ကွဲလွဲမှုများအတွက် တွေးခေါ်မှုစမ်းသပ်ခြင်း သည် လူဦးရေကွဲလွဲမှု၏ null hypothesis ကို ငြင်းပယ်ခြင်း ရှိ၊မရှိ ဆုံးဖြတ်ရန် အသုံးပြုသည့် ကိန်းဂဏန်းဆိုင်ရာ နည်းလမ်းတစ်ခုဖြစ်သည်။ တစ်နည်းဆိုရသော်၊ လူဦးရေ၏ကွဲလွဲမှုတန်ဖိုးနှင့်ပတ်သက်သည့် အယူအဆကွဲလွဲမှုကို ငြင်းဆိုရန် သို့မဟုတ် လက်ခံရန် ကွဲလွဲမှုယူဆချက်စမ်းသပ်ခြင်းကို အသုံးပြုသည်။

အတိအကျအားဖြင့်၊ ကွဲလွဲမှုများအတွက် သီအိုရီစမ်းသပ်မှုကိန်းဂဏန်းတန်ဖိုးနှင့် ရွေးချယ်ထားသော အရေးပါမှုအဆင့်ပေါ်မူတည်၍ null hypothesis ကို ငြင်းပယ်ခြင်း သို့မဟုတ် လက်ခံပါသည်။

သီအိုရီစစ်ဆေးမှုကို အမည်များစွာဖြင့် လုပ်ဆောင်ကြောင်း မှတ်သားထားပါ၊ ၎င်းကို အယူအဆ ဆန့်ကျင်ဘက်များ၊ သီအိုရီစမ်းသပ်ခြင်း သို့မဟုတ် အရေးပါမှု စမ်းသပ်ခြင်းဟုလည်း ခေါ်နိုင်သည်။

ကွဲလွဲမှုများအတွက် Hypothesis Testing Formula

ကွဲလွဲမှုများအတွက် သီအိုရီစမ်းသပ်မှု ကိန်းဂဏန်းသည် နမူနာအရွယ်အစား အနုတ်လက္ခဏာကွဲလွဲမှု၏ တစ်ကြိမ်နှင့် လူဦးရေကွဲလွဲမှု၏ အဆိုပြုထားသော တန်ဖိုးအားဖြင့် ပိုင်းခြားသည့် ကွာခြားချက်နှင့် ညီမျှသည်။ ကွဲလွဲမှုအတွက် သီအိုရီစမ်းသပ်မှု ကိန်းဂဏန်းတွင် ချီစတုရန်း ဖြန့်ဖြူးမှု ရှိသည်။

ထို့ကြောင့် ကွဲလွဲမှုများအတွက် hypothesis test statistic ကို တွက်ချက်ရန် ဖော်မြူလာ မှာ အောက်ပါအတိုင်းဖြစ်သည် ။

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

ရွှေ-

$\chi^2$

Chi-square ဖြန့်ဝေမှုပါရှိသော ကွဲလွဲမှုများအတွက် သီအိုရီစမ်းသပ်မှု ကိန်းဂဏန်းဖြစ်သည်။
$n$

နမူနာအရွယ်အစားဖြစ်သည်။
$s^2$

နမူနာကွဲလွဲမှုဖြစ်သည်။
$\sigma^2$

အဆိုပြုထားသော လူဦးရေကွဲလွဲမှုဖြစ်သည်။

ကိန်းဂဏန်းရလဒ်ကို အဓိပ္ပာယ်ဖွင့်ဆိုရန်၊ ရရှိသောတန်ဖိုးကို စမ်းသပ်မှု၏ အရေးကြီးသောတန်ဖိုးနှင့် နှိုင်းယှဉ်ရမည်ဖြစ်သည်။

ကွဲလွဲမှုများအတွက် သီအိုရီစမ်းသပ်မှုတွင် အမြီးနှစ်ကြောင်းပါပါက၊ ကိန်းဂဏန်းသည် အရေးကြီးသောတန်ဖိုးထက် ကြီးနေပါက null hypothesis ကို ပယ်ချပါသည်။
$\chi_{1-\alpha/2|n-1}^2$

သို့မဟုတ် အရေးကြီးသောတန်ဖိုးထက် နည်းနေပါက၊

$\chi_{\alpha/2|n-1}$

.
ကွဲလွဲမှုများအတွက် သီအိုရီစစ်ဆေးမှုသည် မှန်ကန်သောအမြီးနှင့်ကိုက်ညီပါက၊ ကိန်းဂဏန်းသည် အရေးကြီးသောတန်ဖိုးထက် ကြီးနေပါက null hypothesis ကို ပယ်ချသည်
$\chi_{1-\alpha|n-1}^2$

.
ကွဲလွဲမှုများအတွက် သီအိုရီစစ်ဆေးမှုသည် ဘယ်ဘက်အမြီးနှင့် ကိုက်ညီပါက၊ ကိန်းဂဏန်းသည် အရေးကြီးသောတန်ဖိုးထက်နည်းပါက ကိန်းဂဏာန်းအယူအဆကို ပယ်ချမည်
$\chi_{\alpha|n-1}$

.

$\begin{array}{l}H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha/2|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si }\chi^2<\chi^2_{\alpha/2|n-1}\text{ se rechaza } H_0 \\[3ex]H_1: \sigma^2> \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2< \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2<\chi^2_{\alpha|n-1}\text{ se rechaza } H_0\end{array}$

ကွဲလွဲမှုအတွက် အရေးကြီးသော ယူဆချက် စမ်းသပ်မှုတန်ဖိုးများကို chi-square ဖြန့်ချီရေးဇယားမှ ရယူပါသည်။ Chi-square ဖြန့်ဖြူးမှုအတွက် လွတ်လပ်မှုဒီဂရီများသည် နမူနာအရွယ်အစား အနုတ် 1 ဖြစ်ကြောင်း သတိပြုပါ။

ကွဲလွဲမှုအတွက် Hypothesis Testing ၏ လက်တွေ့ကမ္ဘာနမူနာ

ကွဲလွဲမှုယူဆချက်စမ်းသပ်ခြင်း၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ၎င်း၏ဖော်မြူလာသည် အဘယ်အရာဖြစ်သည်ကို ကြည့်ရှုပြီးနောက်၊ သဘောတရားကို ပေါင်းစပ်ပြီး အပြီးသတ်ရန် ခိုင်မာသောဥပမာတစ်ခုကို ကျွန်ုပ်တို့တွေ့ရပါမည်။

စက်ရုံတစ်ရုံတွင် တိကျမှုမြင့်မားသော ကားတစ်စီးအတွက် အစိတ်အပိုင်းများကို ထုတ်လုပ်သည့် စက်တစ်ခုရှိသည်။ သို့သော်လည်း ၎င်းသည် အဝေးသို့ ရွေ့သွားကာ ယခုအခါ 8 mm ² ထက်ကြီးသော ကွာဟချက်ရှိသော အစိတ်အပိုင်းများကို ထုတ်လုပ်နေပြီဟု သံသယဖြစ်ဖွယ်ရှိသည်။ ဤယူဆချက်ကို ချေပရန်အတွက် နမူနာ 25 ခုကို ခွဲခြမ်းစိတ်ဖြာပြီး ၎င်း၏နမူနာကွဲလွဲမှုသည် 9.1 mm ² ဖြစ်သည်။ ကနဦးယူဆချက်အား သိသာထင်ရှားသောအဆင့် α=0.05 ဖြင့် ပယ်ချနိုင်ပါသလား။

ဤ varianance hypothesis test အတွက် null hypothesis နှင့် အခြား hypothesis မှာ အောက်ပါအတိုင်းဖြစ်သည် ။

$\begin{cases}H_0: \sigma^2=8 \\[2ex] H_1:\sigma^2>8 \end{cases}” title=” Rendered by QuickLaTeX.com” height=” 65″ width=” 101″ style=” vertical-align: 0px;” > null hypothesis ကို ပယ်ချနိုင်သည်ဖြစ်စေ မဆုံးဖြတ်ရန်၊ အထက်တွင်မြင်ခဲ့ရသော ဖော်မြူလာကို အသုံးပြု၍ ကွဲလွဲမှုအတွက် သီအိုရီစမ်းသပ်မှုကိန်းဂဏန်းကို တွက်ချက်သည်- <p class=$ $\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

$\chi^2=\cfrac{(25-1)\cdot 9,1}{8}$

$\chi^2=27,3$

ယခု ကျွန်ုပ်တို့သည် Chi-square ဖြန့်ဖြူးမှုဇယားရှိ 24 ဒီဂရီ လွတ်လပ်မှုနှင့် အရေးပါမှုအဆင့် α=0.05 အတွက် ညာဘက်အမြီးနှင့် သက်ဆိုင်သည့် အရေးကြီးသောတန်ဖိုးကို ရှာဖွေနေသည်-

$\begin{array}{c}\chi^2_{1-\alpha|n-1}=\ \color{orange}\bm{?}\color{black}\\[2ex]\chi^2_{0,95|24}=36,415\end{array}$

ထို့ကြောင့် တွက်ချက်ထားသော ကိန်းဂဏန်းသည် စမ်းသပ်မှု၏ အရေးပါသောတန်ဖိုးထက် နည်းသောကြောင့် ကွဲလွဲမှုယူဆချက်စမ်းသပ်မှု၏ null hypothesis ကို ပယ်ချမည်မဟုတ်သော်လည်း အခြားယူဆချက်အား ပယ်ချပါသည်။

$27,3<36,415 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{No se rechaza } H_0$

➤ ကြည့်ပါ- လူဦးရေအတွက် တွေးခေါ်မှုစမ်းသပ်ခြင်းဆိုလိုသည်။
➤ ကြည့်ပါ- လူဦးရေအချိုးအစားအတွက် သီအိုရီစစ်ဆေးမှု

လူဦးရေနှစ်ခု၏ ကွဲလွဲမှုများအတွက် သီအိုရီစစ်ဆေးမှု

ကွဲပြားသောလူဦးရေနှစ်ခု၏ကွဲလွဲမှု တူညီသည်ဟူသော အယူအဆကွဲလွဲမှုကို ငြင်းပယ်ရန် သို့မဟုတ် လက်ခံရန် အယူအဆနှစ်ခု စမ်းသပ်ခြင်းကို အသုံးပြုသည်။

ထို့ကြောင့် လူဦးရေနှစ်ခု၏ကွဲပြားမှုအပေါ် သီအိုရီစမ်းသပ်မှု၏ null hypothesis သည် အမြဲတမ်းအောက်ပါအတိုင်းဖြစ်သည်-

$H_0: \sigma^2_1=\sigma^2_2$

နှင့် အခြားယူဆချက် သည် ရွေးချယ်စရာ သုံးခုထဲမှ တစ်ခု ဖြစ်နိုင်သည် ။

$\begin{array}{l}H_1:\sigma^2_1\neq \sigma^2_2\\[2ex]H_1:\sigma^2_1>\sigma^2_2\\[2ex]H_1:\sigma^2_1<\sigma^2_2\end{array}$

ဤကိစ္စတွင်၊ လူဦးရေနှစ်ခု၏ကွဲလွဲမှုအတွက် သီအိုရီစမ်းသပ်ကိန်းဂဏန်းကို တွက်ချက်ရန် ဖော်မြူလာမှာ-

$F=\cfrac{s_1^2}{s_2^2}$

ရွှေ-

$F$

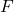
F ဖြန့်ဝေမှု နောက်ဆက်တွဲဖြစ်သော လူဦးရေနှစ်ခု၏ကွဲလွဲမှုများအတွက် သီအိုရီစမ်းသပ်မှု ကိန်းဂဏန်းဖြစ်ပါသည်။
$\sigma_1^2$

လူဦးရေ ကွဲပြားမှု ၁။
$\sigma_2^2$

လူဦးရေ ကွဲပြားမှု ၂။
$s_1^2$

နမူနာ 1 ၏ကွဲလွဲမှုဖြစ်သည်။
$s_2^2$

နမူနာ 2 ၏ကွဲလွဲမှုဖြစ်သည်။
$n_1$

နမူနာအရွယ်အစား 1 ဖြစ်ပါတယ်။
$n_2$

နမူနာအရွယ်အစား 2 ဖြစ်ပါတယ်။

Snedecor F ဖြန့်ဝေမှုသည် အချိုးညီညီမဟုတ်သည့်အတွက်၊ အောက်ပါစံနှုန်းများအပေါ်အခြေခံ၍ null hypothesis ကို ပယ်ချသည်-

[latex]\begin{array}{l}H_1- \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{longrightarrow}\color{black} \text{Si } F>F_{ 1-\alpha/2|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{longrightarrow }\color{black} \text{ အကယ်၍ }F \sigma_2^2 \ \color{orange}\bm{longrightarrow}\color{black} \text{If } F>F_{1-\alpha|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2< \sigma_2^2 \color{orange}\bm{longrightarrow}\color{black} \text{Si } F

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။