ဂျီဩမေတြီ ဖြန့်ဖြူးမှု မိတ်ဆက်

ဂျီဩမေတြီ ဖြန့်ဝေမှုသည် Bernoulli စမ်းသပ်မှု ဆက်တိုက်တွင် ပထမဆုံး အောင်မြင်မှု မကြုံမီ အချို့သော ကျရှုံးမှု အများအပြားကို တွေ့ကြုံရနိုင်ခြေကို ဖော်ပြသည်။

Bernoulli စမ်းသပ်မှု သည် ဖြစ်နိုင်ချေ ရလဒ် နှစ်ခုသာရှိသော စမ်းသပ်မှုဖြစ်ပြီး – “ အောင်မြင်မှု” သို့မဟုတ် “ ကျရှုံးခြင်း” – စမ်းသပ်မှုပြုလုပ်သည့်အချိန်တိုင်း အောင်မြင်နိုင်ခြေသည် အတူတူပင်ဖြစ်ပါသည်။

Bernoulli စာစီစာကုံး၏ ဥပမာတစ်ခုသည် အကြွေစေ့ပစ်ခြင်း ဖြစ်သည်။ ဒင်္ဂါးသည် ခေါင်းနှစ်လုံးပေါ်တွင်သာ ဆင်းသက်နိုင်သည် (ကျွန်ုပ်တို့သည် ခေါင်းများကို “ တိုက်သည်” နှင့် “ ပျက်ကွက်” ဟု ခေါ်နိုင်သည်) နှင့် ဒင်္ဂါးပြားသည် မျှတသည်ဟု ယူဆကာ လှန်လိုက်တိုင်းတွင် အောင်မြင်နိုင်ခြေသည် 0.5 ဖြစ်သည်။

ကျပန်းပြောင်းလဲနိုင်သော X သည် ဂျီဩမေတြီဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်ပါက၊ ပထမအောင်မြင်မှုမတွေ့ကြုံမီ k ကျရှုံးမှုဖြစ်နိုင်ခြေကို အောက်ပါဖော်မြူလာဖြင့် ရှာတွေ့နိုင်သည်-

P(X=k) = (1-p) ^kp

ရွှေ-

• k: ပထမမအောင်မြင်မီ ကျရှုံးမှုအရေအတွက်
• p- စမ်းသပ်မှုတစ်ခုစီတွင် အောင်မြင်မှုဖြစ်နိုင်ခြေ

ဥပမာအားဖြင့်၊ အကြွေစေ့ခေါင်းပေါ်မတက်မချင်း အကြိမ်မည်မျှလှန်ရမည်ကို သိချင်သည်ဆိုပါစို့။ 0၊ 1၊ 2၊ 3 ကျရှုံးမှုများ စသည်တို့ကို တွေ့ကြုံခံစားရနိုင်ခြေကို ဆုံးဖြတ်ရန် အထက်ဖော်ပြပါ ဖော်မြူလာကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။ ဒင်္ဂါးသည် ခေါင်းပေါ်မတက်မီ၊

မှတ်ချက်- ဒင်္ဂါးသည် ပထမဦးစွာပစ်ခြင်းတွင် ခေါင်းတက်လာပါက အကြွေစေ့သည် 0 “ ကျရှုံးခြင်း” ကို တွေ့ကြုံခံစားရနိုင်သည်။

P(X=0) = (1-.5) ⁰ (.5) = 0.5

P(X=1) = (1-.5) ¹ (.5) = 0.25

P(X=2) = (1-.5) ² (.5) = 0.125

P(X=3) = (1-0.5) ³ (0.5) = 0.0625

ကျွန်ုပ်တို့သည် အဆုံးမရှိအထိ ပစ်လွှတ်သည့် မည်သည့်အကြွေစေ့၏ ဖြစ်နိုင်ခြေကိုမဆို တွက်ချက်နိုင်သည်။ ထို့နောက် ဤဖြစ်နိုင်ချေ ဖြန့်ဖြူးမှုကို မြင်သာစေရန် ရိုးရှင်းသော histogram တစ်ခုကို ဖန်တီးသည်-

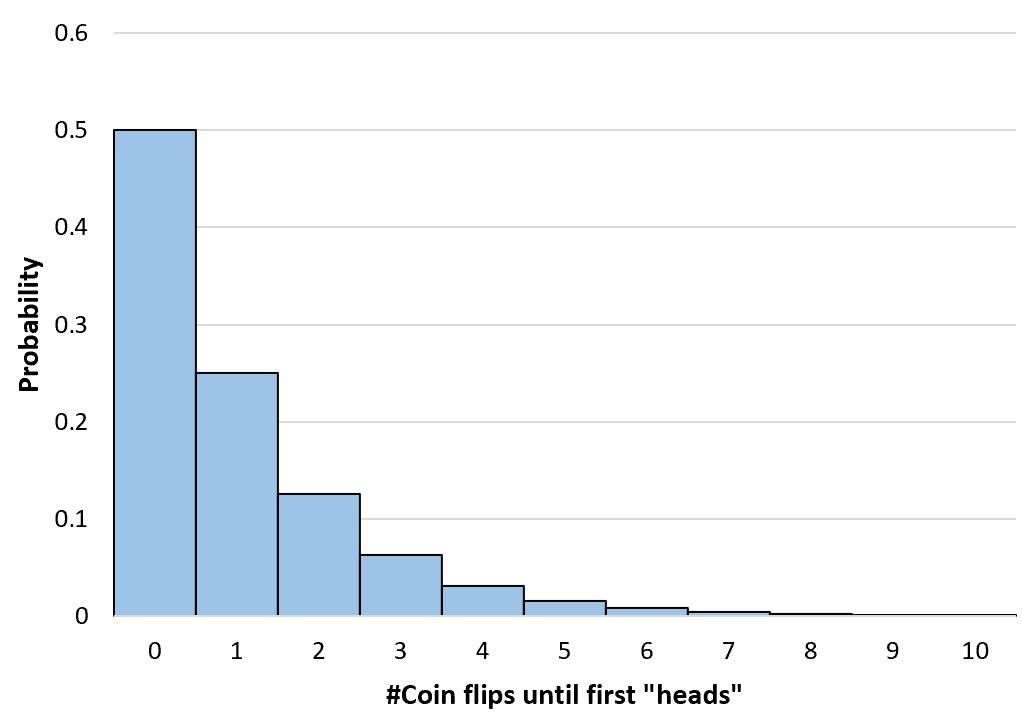
တိုးပွားလာသော ဂျီဩမေတြီဖြစ်နိုင်ခြေများကို တွက်ချက်ခြင်း။

အောက်ပါဖော်မြူလာဖြင့် ပထမအောင်မြင်မှုကို ရှာမတွေ့မချင်း ကျွန်ုပ်တို့သည် k သို့မဟုတ် နည်းပါးသော ကျရှုံးမှုများ ကြုံတွေ့နေရသည့် စုစည်းဖြစ်နိုင်ခြေ –

P(X≤k) = 1 – (1-p) ^k+1

ရွှေ-

• k: ပထမမအောင်မြင်မီ ကျရှုံးမှုအရေအတွက်
• p- စမ်းသပ်မှုတစ်ခုစီတွင် အောင်မြင်မှုဖြစ်နိုင်ခြေ

ဥပမာအားဖြင့်၊ အကြွေစေ့ခေါင်းပေါ်မတက်မီ သုံးကြိမ် သို့မဟုတ် ထိုနည်းသော “ လွမ်းဆွတ်မှုများ” ယူရမည့် ဖြစ်နိုင်ခြေကို ကျွန်ုပ်တို့ သိလိုသည်ဆိုပါစို့။ ဤဖြစ်နိုင်ခြေကို တွက်ချက်ရန် အောက်ပါဖော်မြူလာကို ကျွန်ုပ်တို့ အသုံးပြုပါမည်။

P(X≤3) = 1 – (1-0.5) ³⁺¹ = 0.9375

အလားတူ ဖော်မြူလာကို အသုံးပြု၍ တိုးပွားလာနိုင်သည့် ဖြစ်နိုင်ခြေတစ်ခုစီကို ကျွန်ုပ်တို့ တွက်ချက်နိုင်သည်-

P(X≤0) = 1 – (1-.5) ⁰⁺¹ = 0.5

P(X≤1) = 1 – (1-0.5) ¹⁺¹ = 0.75

P(X≤2) = 1 – (1-0.5) ²⁺¹ = 0.875

အကြွေစေ့များကို အဆုံးမရှိအထိ လွှင့်ပစ်သည့် မည်သည့်အရေအတွက်အတွက်မဆို ဤစုပြုံဖြစ်နိုင်ခြေများကို တွက်ချက်နိုင်ပါသည်။ ထို့နောက် ဤစုပြုံဖြစ်နိုင်ခြေဖြန့်ဝေမှုကို မြင်သာစေရန် ဟီစတိုဂရမ်တစ်ခု ဖန်တီးနိုင်သည်-

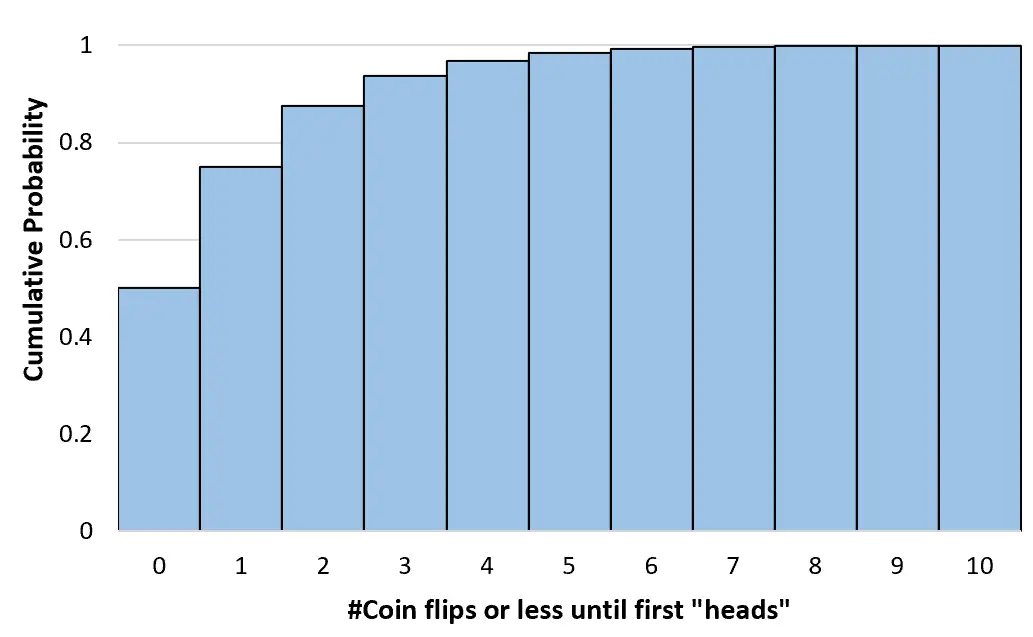
ဂျီဩမေတြီဖြန့်ဖြူးခြင်း၏ ဂုဏ်သတ္တိများ

ဂျီဩမေတြီ ဖြန့်ဝေမှုတွင် အောက်ပါ ဂုဏ်သတ္တိများ ရှိသည်။

ဖြန့်ဖြူးမှု၏ပျမ်းမျှမှာ (1-p) / p ဖြစ်သည်။

ဖြန့်ဖြူးမှု၏ကွဲလွဲမှုသည် (1-p) / p ² ဖြစ်သည်။

ဥပမာအားဖြင့်:

အမြီးများမဆင်းမီ အကြွေစေ့ဆီသို့ အကြွေစေ့ဆီသို့ ပျမ်းမျှ အကြိမ်အရေအတွက် (1-p) / p = (1-.5) / .5 = 1 ဖြစ်လိမ့်မည်။

ဦးခေါင်းပေါ်ရောက်သည်အထိ လွှင့်ပစ်သည့်အရေအတွက်၏ ကွဲလွဲမှုမှာ (1-p)/ ^p2 =(1-.5)/ ဖြစ်သည်။ ^၅၂ = ၂ ။

ဂျီဩမေတြီ ဖြန့်ဝေမှု အလေ့အကျင့် ပြဿနာများ

ဂျီဩမေတြီဖြန့်ဖြူးခြင်းဆိုင်ရာ အသိပညာကို စမ်းသပ်ရန် အောက်ပါအလေ့အကျင့်ပြဿနာများကို အသုံးပြုပါ။

မှတ်ချက်- ဤမေးခွန်းများအတွက် အဖြေများကို တွက်ချက်ရန် ဂျီဩမေတြီ ဖြန့်ဝေမှုဂဏန်းတွက်စက်ကို ကျွန်ုပ်တို့ အသုံးပြုပါမည်။

ပြဿနာ ၁

မေးခွန်း- သုတေသီတစ်ဦးသည် ဥပဒေတစ်ရပ်ရပ်ကို ထောက်ခံခြင်းရှိမရှိ လူများကို မေးမြန်းရန် စာကြည့်တိုက်အပြင်ဘက်တွင် စောင့်ဆိုင်းနေပါသည်။ ဥပဒေကို ပံ့ပိုးပေးထားသည့် ပုဂ္ဂိုလ်တစ်ဦးဖြစ်နိုင်ခြေမှာ p = 0.2 ဖြစ်သည်။ သုတေသီ ဟောပြောသူ စတုတ္ထပုဂ္ဂိုလ်သည် ဥပဒေကို ထောက်ခံသူဖြစ်နိုင်ခြေ မည်မျှရှိသနည်း။

အဖြေ- ပထမမအောင်မြင်မီအထိ “ကျရှုံးမှု” အရေအတွက်- ဆိုလိုသည်မှာ၊ ပထမလူက ထောက်ခံသည့်တိုင်အောင် ဥပဒေကို မထောက်ခံသူအရေအတွက်- 3 ဖြစ်သည်။ ထို့ကြောင့် p = 0.2 နှင့် x ရှိသော ဂျီဩမေတြီဖြန့်ဖြူးဂဏန်းတွက်စက်ကို အသုံးပြုရာတွင်၊ = 3 ကြိမ်ပျက်ကွက်၊ P(X=3) = 0.10240 တွေ့သည်။

ပြဿနာ ၂

မေးခွန်း- သုတေသီတစ်ဦးသည် ဥပဒေတစ်ရပ်ရပ်ကို ထောက်ခံခြင်းရှိမရှိ လူများကို မေးမြန်းရန် စာကြည့်တိုက်အပြင်ဘက်တွင် စောင့်ဆိုင်းနေပါသည်။ ဥပဒေကို ပံ့ပိုးပေးထားသည့် ပုဂ္ဂိုလ်တစ်ဦးဖြစ်နိုင်ခြေမှာ p = 0.2 ဖြစ်သည်။ သုတေသီသည် ဥပဒေကို ထောက်ခံသူ တစ်ဦးကို ရှာဖွေရန် လူလေးဦးထက် ပို၍ စကားပြောဆိုရန် ဖြစ်နိုင်ခြေ မည်မျှရှိသနည်း။

အဖြေ- p = 0.2 နှင့် x = 4 ကျရှုံးမှုများပါရှိသော ဂျီဩမေတြီဖြန့်ချီရေးဂဏန်းတွက်စက်ကို အသုံးပြု၍ P(X>4) = 0.32768 ကို ကျွန်ုပ်တို့တွေ့ရှိသည်။

ပြဿနာ ၃

မေးခွန်း- သုတေသီတစ်ဦးသည် ဥပဒေတစ်ရပ်ရပ်ကို ထောက်ခံခြင်းရှိမရှိ လူများကို မေးမြန်းရန် စာကြည့်တိုက်အပြင်ဘက်တွင် စောင့်ဆိုင်းနေပါသည်။ ဥပဒေကို ပံ့ပိုးပေးထားသည့် ပုဂ္ဂိုလ်တစ်ဦးဖြစ်နိုင်ခြေမှာ p = 0.2 ဖြစ်သည်။ သုတေသီသည် ဥပဒေအား ထောက်ခံသူတစ်ဦးကို ရှာမတွေ့မချင်း သူနှင့် စကားပြောရန် လိုအပ်သည့် လူအရေအတွက် မည်မျှရှိမည်နည်း။

အဖြေ- ဂျီဩမေတြီဖြန့်ဖြူးမှု၏ဆိုလိုသည်မှာ (1-p) / p ဖြစ်ကြောင်း မှတ်သားပါ။ ဤအခြေအနေတွင် ပျမ်းမျှ (1-.2) / .2 = 4 ဖြစ်လိမ့်မည်။