မြို့ပတ်ကားချပ်

အားဖြင့် Benjamin Anderson ဩဂုတ် 5, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင်၊ pie chart သည် ဘာလဲ၊ pie chart တစ်ခုကို တည်ဆောက်ပုံ၊ နှင့် ဤဇယားအမျိုးအစားအတွက် အဆင့်ဆင့် လေ့ကျင့်ခန်းကို လေ့လာပါမည်။ ထို့အပြင်၊ အဝိုင်းပုံဇယားများ၏ လက္ခဏာရပ်များကို သင်မြင်နိုင်မည်ဖြစ်သည်။

အဝိုင်းပုံဇယားဆိုတာ ဘာလဲ။

pie chart ၊ pie chart ဟုလည်း ခေါ်သည် ၊ သည် ရာခိုင်နှုန်းများနှင့် အချိုးများကို အမြင်အားဖြင့် ကိုယ်စားပြုရန် အသုံးပြုသည့် ကိန်းဂဏန်းဇယား အမျိုးအစားတစ်ခုဖြစ်သည်။ ပို၍တိကျသည်မှာ၊ အဝိုင်းပုံဇယားတစ်ခုတွင် ဒေတာကို စက်ဝိုင်းတစ်ခု၏အပိုင်းများဖြင့် ကိုယ်စားပြုသည်၊ ထို့ကြောင့် ဒိန်ခဲ တစ်ခုစီ၏ထောင့်သည် ၎င်း၏ကြိမ်နှုန်းနှင့်အချိုးကျနေစေရန်။

ထို့ကြောင့်၊ တန်ဖိုးတစ်ခု၏ ကြိမ်နှုန်းမြင့်လေ၊ ၎င်းသည် အဝိုင်းပုံဇယားတွင် မျှဝေမှု ပိုများလေဖြစ်သည်။

စာရင်းဇယားများတွင်၊ ပုံဇယားများသည် ဂရပ်တစ်ခုပေါ်ရှိ အရည်အသွေးဆိုင်ရာ အချက်အလက်များကို ကိုယ်စားပြုရန်အတွက် အလွန်အသုံးဝင်ပြီး ၎င်းတို့ကိုလည်း လျင်မြန်စွာ ကောက်ချက်ဆွဲနိုင်စေပါသည်။

pie chart တွင် pie chart၊ pizza chart၊ pie chart၊ cheese chart သို့မဟုတ် 360 degree chart ကဲ့သို့သော အမျိုးမျိုးသောအမည်များရှိကြောင်း သတိပြုသင့်သည်။

အဝိုင်းပုံဇယားလုပ်နည်း

pie chart တစ်ခု၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်အား ဤကဏ္ဍတွင် ဤအမျိုးအစား၏ ဇယားကွက်ဖန်တီးနည်းကို ပြသသည်-

ကိန်းဂဏန်းအချက်အလက်ကို စုဆောင်းပြီး သက်ဆိုင်ရာ ကြိမ်နှုန်းဇယားကို ပြင်ဆင်ပါ။
အောက်ပါပုံသေနည်းဖြင့် ဂရပ်၏ကဏ္ဍတစ်ခုစီ၏ထောင့်ကို တွက်ချက်ပါ။

$\alpha_i= f_i \cdot \cfrac{360^o}{N}$

ရွှေ

$\alpha_i$

ကဏ္ဍ i ၏ ထောင့်၊

$f_i$

၎င်း၏ပကတိကြိမ်နှုန်းနှင့်

$N$

စုစုပေါင်းဒေတာ။

တွက်ချက်ထားသောထောင့်များမှ၊ protractor အသုံးပြု၍ စက်ဝိုင်းပုံဂရပ်ပေါ်တွင် ကဏ္ဍများကို ကိုယ်စားပြုပါ။
အောက်ပါပုံသေနည်းဖြင့် ကဏ္ဍတစ်ခုစီ၏ ရာခိုင်နှုန်းကို တွက်ချက်ပါ။

$\%_i= f_i \cdot \cfrac{100}{N}$

ရွှေ

$\%_i$

ကဏ္ဍ i ရာခိုင်နှုန်း၊

$f_i$

၎င်း၏ပကတိကြိမ်နှုန်းနှင့်

$N$

စုစုပေါင်းဒေတာ။

ကဏ္ဍတစ်ခုစီ၏ ရာခိုင်နှုန်းကို ဂရပ်ပေါ်တွင် ညွှန်ပြပါ။

Pie Chart နမူနာ

စက်ဝိုင်းပုံဇယားကို ဘယ်လိုတည်ဆောက်ထားလဲဆိုတာ သိနိုင်စေဖို့ အောက်မှာ အဆင့်ဆင့် ရှင်းပြထားတဲ့ ဥပမာတစ်ခုနဲ့ မိတ်ဆက်ပေးပါရစေ။

လူ 50 ကို ၎င်းတို့၏ စိတ်ကြိုက်မြို့အကြောင်း မေးမြန်းခဲ့ပြီး အချက်အလက်များကို အောက်ပါဇယားတွင် ပြုစုခဲ့သည်။ ဤကိန်းဂဏန်းအချက်အလက်ကို အဝိုင်းပုံဇယားတွင် ရေးဆွဲပါ။

ပထမဆုံးအနေနဲ့ ဒိန်ခဲ တစ်ခုစီနဲ့ ကိုက်ညီတဲ့ ထောင့်ကို ရှာရပါမယ်။ ဒါကိုလုပ်ဖို့၊ အောက်ပါပုံသေနည်းကို သုံးပါတယ်။

$\alpha_i = f_i \cdot \cfrac{360^o}{N}$

ရွှေ

$\alpha_i$

ကဏ္ဍတစ်ခုစီ၏ ထောင့်၊

$f_i$

၎င်း၏ကြိမ်နှုန်းနှင့်

$N$

စုစုပေါင်းလေ့လာတွေ့ရှိချက်အရေအတွက်။

ဥပမာအနေဖြင့်၊ ဒေတာဇယားရှိ ပထမတန်ဖိုးနှင့် သက်ဆိုင်သောထောင့်ကို တွက်ချက်သည်-

$\alpha_{Londres}=16 \cdot \cfrac{360^o}{50} = 115,2^o$

ထောင့်ကိုသိသည်နှင့်၊ protractor ကိုအသုံးပြု၍ စက်ဝိုင်းပုံကဏ္ဍကို ရိုးရှင်းစွာကိုယ်စားပြုသည်-

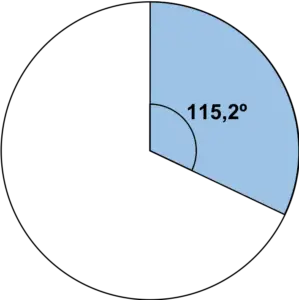
ကျွန်ုပ်တို့သည် ဇယားရှိ တန်ဖိုးများအားလုံးအတွက် တူညီသောအဆင့်ကို ပြန်လုပ်သည်-

$\alpha_{Paris}=12 \cdot \cfrac{360^o}{50}=86,4^o$

$\alpha_{Nueva \ York}=9\cdot \cfrac{360^o}{50}=64,8^o$

$\alpha_{Roma}= 7 \cdot \cfrac{360^o}{50} = 50,4^o$

$\alpha_{Otras}=6 \cdot \cfrac{360^o}{50} = 43,2^o$

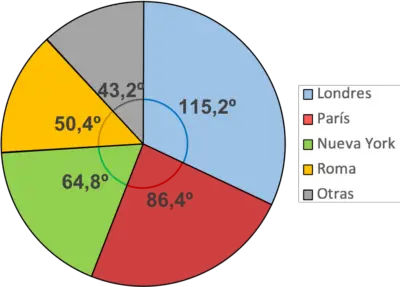
ဂရပ်ကို နားလည်လွယ်စေရန် ကဏ္ဍတစ်ခုစီကို အရောင်တစ်ခုစီခြယ်ရန် အကြံပြုထားသည်။ အလားတူ၊ ပုံတွင် အရောင်တစ်ခုစီ၏ အဓိပ္ပါယ်ကိုပြသရန် ဒဏ္ဍာရီတစ်ခုကို ထည့်သင့်သည်။

ဒိန်ခဲများကို ပုံဆွဲပြီးနောက်၊ ၎င်းကို ပုံတွင်ထည့်ရန် တစ်ခုစီ၏ ရာခိုင်နှုန်းကို တွက်ချက်ရန် လိုအပ်သည်။ ဒါကိုလုပ်ဖို့၊ အောက်ပါပုံသေနည်းကို သုံးပါတယ်။

$\%_i = f_i \cdot \cfrac{100}{N}$

ရွှေ

$\%_i$

ကဏ္ဍတစ်ခုစီ၏ ရာခိုင်နှုန်း၊

$f_i$

၎င်း၏ကြိမ်နှုန်းနှင့်

$N$

စာရင်းအင်းလေ့လာမှုမှဒေတာစုစုပေါင်းအရေအတွက်။

ထို့ကြောင့် ကဏ္ဍတစ်ခုစီ၏ ရာခိုင်နှုန်းသည်-

$\%_{Londres} \cdot \cfrac{100}{N}=16\cdot \cfrac{100}{50}=32\%$

$\%_{Paris}=12 \cdot \cfrac{100}{50}=24\%$

$\%_{Nueva \ York}}=9\cdot\cfrac{100}{50}=18\%$

$\%_{Roma}}=7\cdot\cfrac{100}{50}=14\%$

$\%_{Otras}=6\cdot\cfrac{100}{50}=12\%$

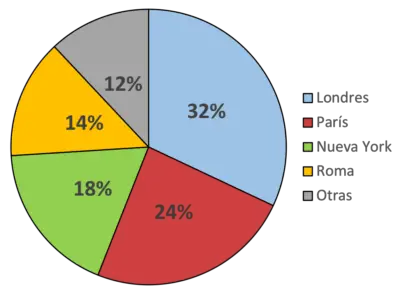
ဤအဝိုင်းပုံဇယားဖြင့် ဥပမာအားဖြင့်၊ အပြာရောင်သည် လန်ဒန်မြို့ကို ကိုယ်စားပြုပြီး လူအများစုနှစ်သက်သည့်နေရာ (32%) ဖြစ်သည်ဟု ကျွန်ုပ်တို့ညွှန်ပြပါသည်။ အခြားတစ်ဖက်တွင်မူ အစိမ်းသည် စစ်တမ်းကောက်ယူသူ ၁၈ ရာခိုင်နှုန်း၏ အကြိုက်ဆုံးမြို့ဖြစ်သည့် နယူးယောက်ကို ကိုယ်စားပြုသည်။

Pie Chart အင်္ဂါရပ်များ

Camembert ၏ထူးခြားချက်များမှာအောက်ပါအတိုင်းဖြစ်သည်။

အဝိုင်းပုံဇယားသည် အရည်အသွေးကောင်းမွန်သောဒေတာကို ကိုယ်စားပြုရန်အတွက် အလွန်အသုံးဝင်သည်။
သို့ရာတွင်၊ ကိန်းဂဏန်းကိန်းရှင်များ သို့မဟုတ် အချိန်စီးရီးများကို ကိုယ်စားပြုရန် ပိုမိုသင့်လျော်သော အခြားကိန်းဂဏန်းဂရပ်များ ရှိပါသည်။
ထို့အပြင်၊ ကွက်ကွက်ဇယားတစ်ခုတွင် ကိန်းရှင်တစ်ခုတည်းကိုသာ ကိုယ်စားပြုနိုင်ပြီး ကိန်းရှင်များကို နှိုင်းယှဉ်ရန်ခက်ခဲစေသည်။
အဝိုင်းပုံဇယားသည် အလွန်အမြင်သာသောကြောင့် လျင်မြန်သောခွဲခြမ်းစိတ်ဖြာမှုနှင့် ကောက်ချက်ချနိုင်စေပါသည်။
ကဏ္ဍများစွာရှိသည် သို့မဟုတ် အချို့သည် အလွန်သေးငယ်သောအခါဇယားကိုဖတ်ရန်ခက်ခဲသည်။ ထိုသို့သောအခြေအနေမျိုးတွင်၊ သေးငယ်သောကဏ္ဍများကို “ အခြားသူများ” ဟုခေါ်သော ကဏ္ဍတစ်ခုတည်းတွင် အုပ်စုဖွဲ့ရန် အကြံပြုထားသည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။

အဝိုင်းပုံဇယားဆိုတာ ဘာလဲ။

အဝိုင်းပုံဇယားလုပ်နည်း

Pie Chart နမူနာ

Pie Chart အင်္ဂါရပ်များ

စာရေးသူအကြောင်း

Benjamin Anderson

မှတ်ချက်တစ်ခုထည့်ပါ။