ဖက်ရှင် (စာရင်းအင်း)
ဤဆောင်းပါးသည် စာရင်းဇယားများတွင် မည်သည့်မုဒ်ကို ရှင်းပြထားသည်။ အုပ်စုဖွဲ့ဒေတာနှင့် အဖွဲ့မ၀င်သောဒေတာ၊ မတူညီသောမုဒ်အမျိုးအစားများနှင့် ဤစာရင်းအင်းတိုင်းတာမှု၏နမူနာများစွာအတွက် ကိန်းဂဏန်းမုဒ်ကို သင်မည်သို့ရှာဖွေရမည်နည်း။
ကိန်းဂဏန်းစာရင်းဇယားတွင် မုဒ်ဟူသည် အဘယ်နည်း။
စာရင်းဇယားများတွင်၊ မုဒ်သည် အမြင့်ဆုံး ပကတိကြိမ်နှုန်းပါရှိသော ဒေတာအတွဲတွင် တန်ဖိုးဖြစ်သည်၊ ဆိုလိုသည်မှာ မုဒ်သည် ဒေတာအစုတစ်ခုတွင် ထပ်ခါတလဲလဲ အများဆုံးတန်ဖိုးဖြစ်သည်။
ထို့ကြောင့်၊ ကိန်းဂဏန်းအချက်အလက်အစုတစ်ခု၏မုဒ်ကို တွက်ချက်ရန်၊ နမူနာတစ်ခုစီတွင် ဒေတာဒြပ်စင်တစ်ခုစီပေါ်လာသည့်အကြိမ်အရေအတွက်ကို ရိုးရိုးရေတွက်ပြီး ထပ်ခါတလဲလဲ အများဆုံးဒေတာသည် မုဒ်ဖြစ်လိမ့်မည်။
ထပ်ခါတလဲလဲတန်ဖိုးအများစုသည် အများအားဖြင့် ဖြန့်ဝေမှု၏ဗဟိုတွင် ဖြစ်သောကြောင့် ကိန်းဂဏန်းခွဲဝေမှုကို သတ်မှတ်ရန် မုဒ်ကိုအသုံးပြုသည်။
မုဒ်ကို စာရင်းအင်းမုဒ် သို့မဟုတ် မော်ဒယ်တန်ဖိုး ဟုလည်း ဆိုနိုင်သည်။ အလားတူ၊ ဒေတာကို ကြားကာလများအဖြစ် အုပ်စုဖွဲ့သည့်အခါ၊ ထပ်ခါတလဲလဲ ကြားကာလ အများဆုံးမှာ modal interval သို့မဟုတ် modal class ဖြစ်သည်။
ယေဘူယျအားဖြင့်၊ Mo ဟူသော အသုံးအနှုန်းကို ကိန်းဂဏန်းမုဒ်အတွက် သင်္ကေတအဖြစ် အသုံးပြုသည်၊ ဥပမာ၊ ဖြန့်ဖြူးမှုမုဒ် X သည် Mo(X) ဖြစ်သည်။
မုဒ်သည် ဗဟိုအနေအထား၏ ကိန်းဂဏန်းအချက်အလက်များအပြင် အလယ်အလတ်နှင့် ပျမ်းမျှအား အတိုင်းအတာတစ်ခုဖြစ်ကြောင်း မှတ်သားထားပါ။ ဤစာရင်းအင်းဆိုင်ရာ တိုင်းတာမှုတစ်ခုစီ၏ အဓိပ္ပါယ်ကို အောက်တွင် ကြည့်ရှုပါမည်။
စာရင်းဇယားများတွင် မုဒ်အမျိုးအစားများ
စာရင်းဇယားများတွင်၊ အများဆုံးအကြိမ်ကြိမ်တန်ဖိုးများအလိုက် အမျိုးအစားခွဲခြားထားသော မုဒ်များစွာ ရှိပါသည်။
- Unimodal မုဒ် : ထပ်ခါတလဲလဲ အများဆုံးအကြိမ်အရေအတွက် တစ်ခုတည်းသာရှိသည်။ ဥပမာ၊ [၁၊ ၄၊ ၂၊ ၄၊ ၅၊ ၃]။
- Bimodal မုဒ် : ထပ်ခါတလဲလဲ အများဆုံးအကြိမ်အရေအတွက်သည် မတူညီသောတန်ဖိုးနှစ်ခုတွင် ဖြစ်ပေါ်ပြီး တန်ဖိုးနှစ်ခုစလုံးသည် အကြိမ်အရေအတွက် တူညီပါသည်။ ဥပမာ၊ [၂၊ ၆၊ ၇၊ ၂၊ ၃၊ ၆၊ ၉]။
- Multimodal မုဒ် – သုံးမျိုး သို့မဟုတ် ထို့ထက်ပိုသော တန်ဖိုးများသည် ထပ်ခါတလဲလဲ အများဆုံးအကြိမ်အရေအတွက် တူညီသည်။ ဥပမာ၊ [၃၊ ၃၊ ၄၊ ၁၊ ၃၊ ၄၊ ၂၊ ၁၊ ၄၊ ၅၊ ၂၊ ၁]။
စာရင်းအင်းမုဒ်ကို ဘယ်လိုရှာမလဲ။
ဒေတာအတွဲတစ်ခု၏ ကိန်းဂဏန်းစာရင်းအင်းမုဒ်ကို ရှာရန်၊ သင်သည် အောက်ပါအဆင့်များကို လိုက်နာရပါမည်။
- ဒေတာကို စနစ်တကျထားပါ။ ဤအဆင့်သည် မဖြစ်မနေ မလိုအပ်သော်လည်း ဂဏန်းရေတွက်ခြင်းကို ပိုမိုလွယ်ကူစေသည်။
- နံပါတ်တစ်ခုစီတွင် မည်မျှပေါ်လာသည်ကို ရေတွက်ပါ။
- မကြာခဏပေါ်လာသော နံပါတ်သည် ကိန်းဂဏန်းမုဒ်ဖြစ်သည်။
စာရင်းအင်းမုဒ် ဥပမာများ
စာရင်းဇယားများတွင် ဖက်ရှင်၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို ထည့်သွင်းစဉ်းစားခြင်းဖြင့် အယူအဆကို ပိုမိုနားလည်နိုင်စေရန် ဖက်ရှင်အမျိုးအစားတစ်ခုစီ၏ နမူနာကို အောက်တွင် ကြည့်ရှုနိုင်ပါသည်။
unimodal mode ၏ဥပမာ
- အောက်ပါဒေတာအတွဲ၏မုဒ်မှာ အဘယ်နည်း။
![]()
နံပါတ်များကို စီထားခြင်း မရှိသေးသောကြောင့် မုဒ်ကို ရှာရလွယ်ကူစေရန် ဦးစွာ အမိန့်ပေးပါမည်။
![]()
နံပါတ် 2 နှင့် 9 သည် နှစ်ကြိမ်ပေါ်လာသော်လည်း 5 သည် သုံးကြိမ်ထပ်ခါထပ်ခါဖြစ်သည်။ ထို့ကြောင့်၊ ဒေတာစီးရီး၏မုဒ်မှာ နံပါတ် ၅ ဖြစ်သည်။
![]()
bimodal mode ၏ဥပမာ
- အောက်ပါဒေတာအစုံ၏မုဒ်ကို တွက်ချက်ပါ-
![]()
![]()
ပထမဦးစွာ ကျွန်ုပ်တို့သည် နံပါတ်များကို အစဉ်လိုက်ချထားသည်-
![]()
![]()
သင်မြင်သည့်အတိုင်း၊ နံပါတ် 6 နှင့် 8 သည် စုစုပေါင်းအကြိမ်ရေ လေးကြိမ်ပေါ်လာသည်၊ ယင်းသည် ထပ်ခါတလဲလဲအများဆုံးအကြိမ်ဖြစ်သည်။ ထို့ကြောင့်၊ ဤကိစ္စတွင်၊ ၎င်းသည် bimodal မုဒ်ဖြစ်ပြီး နံပါတ်နှစ်ခုသည် dataset ၏မုဒ်ဖြစ်သည်။
![]()
Multimodal mode ၏ဥပမာ
- အောက်ပါဒေတာအစုံမုဒ်ကိုရှာပါ
![]()
![]()
![]()
ဒေတာများစွာရှိသောကြောင့်၊ ရေတွက်ရလွယ်ကူစေရန်အတွက် ၎င်းကို ငယ်စဉ်ကြီးလိုက် စီထားပါသည်-
![]()
![]()
![]()
ထပ်ခါတလဲလဲ အများဆုံး ဂဏန်းများမှာ 20၊ 27 နှင့် 31 ဖြစ်ပြီး ဂဏန်းသုံးလုံးစလုံးကို ငါးကြိမ် ထပ်ခါထပ်ခါ ပြုလုပ်ပါသည်။ ထို့ကြောင့် ဤဥပမာ၏မုဒ်သည် Multimodal ဖြစ်သည်။
![]()
ဖက်ရှင်ဂဏန်းပေါင်းစက်
၎င်း၏မုဒ်ကိုတွက်ချက်ရန် အောက်ပါအွန်လိုင်းဂဏန်းတွက်စက်ထဲသို့ ကိန်းဂဏန်းနမူနာတစ်ခုခုမှ အချက်အလက်ကို ထည့်သွင်းပါ။ ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။
အုပ်စုဖွဲ့ဒေတာအတွက် မုဒ်
ကျွန်ုပ်တို့တွင် ဒေတာများကို ကြားကာလပုံစံဖြင့် အုပ်စုဖွဲ့သည့်အခါ၊ ဒေတာအပိုင်းတစ်ခုစီကို အကြိမ်မည်မျှ ထပ်ခါတလဲလဲ မသိနိုင်သော်လည်း ကြားကာလတစ်ခုစီ၏ ကြိမ်နှုန်းကိုသာ သိပါသည်။
ထို့ကြောင့်၊ ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ထားသော ဒေတာမုဒ်ကို တွက်ချက်ရန်၊ ကျွန်ုပ်တို့သည် အောက်ပါဖော်မြူလာကို အသုံးပြုရပါမည် ။
![]()
ရွှေ-
- L i သည် modal interval (အမြင့်ဆုံး absolute frequency interval) ၏ အနိမ့်ဆုံးကန့်သတ်ချက်ဖြစ်သည်။
- f i သည် modal ကြားကာလ၏ ပကတိကြိမ်နှုန်းဖြစ်သည်။
- f i-1 သည် modal မတိုင်မီ ကြားကာလ၏ ပကတိကြိမ်နှုန်းဖြစ်သည်။
- f i+1 သည် modal ပြီးနောက် ကြားကာလ၏ ပကတိကြိမ်နှုန်းဖြစ်သည်။
- A i သည် modal ကြားကာလ၏ အကျယ်ဖြစ်သည်။
ဥပမာအနေဖြင့်၊ အောက်တွင် ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ထားသော ဒေတာမုဒ်ကို တွက်ချက်ထားသည့် လေ့ကျင့်ခန်းတစ်ခုကို သင်ဖြေရှင်းပြီးပါပြီ-
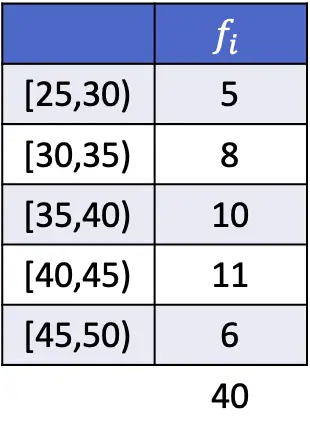
ဤအခြေအနေတွင်၊ modal interval သည် [40,45) ဖြစ်သောကြောင့် ၎င်းသည် အကြီးမားဆုံး absolute frequency နှင့် ကြားကာလဖြစ်သည်။ ထို့ကြောင့်၊ အုပ်စုဖွဲ့ဒေတာအတွက် မုဒ်ဖော်မြူလာ ဘောင်များသည်-
![Rendered by QuickLaTeX.com \begin{array}{c}L_i=40\\[2ex]f_i=11\\[2ex]f_{i-1}=10\\[2ex]f_{i+1}=6\\[2ex]A_i=5\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-85aef7092d3e0c7769ad17b96aae294c_l3.png)
ထို့ကြောင့် ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ထားသော ဒေတာ၏မုဒ်ကို ဆုံးဖြတ်ရန် ဖော်မြူလာကို အသုံးပြုကာ တွက်ချက်မှုကို လုပ်ဆောင်သည်-
![Rendered by QuickLaTeX.com \begin{aligned}Mo & =L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i\\[2ex]& =40+ \cfrac{11-10}{(11-10)+(11-6)}\cdot 5\\[2ex]&=40,83\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-3ee33fdb43267fdcfc6d222ed6798fca_l3.png)
မုဒ်၊ ပျမ်းမျှနှင့် အလယ်အလတ် ကွာခြားချက်
ဤနောက်ဆုံးအပိုင်းတွင် မုဒ်၊ ပျမ်းမျှနှင့် အလယ်အလတ်ကြား ခြားနားချက်ကို ကျွန်ုပ်တို့ မြင်တွေ့ရမည်ဖြစ်သည်။ သုံးခုစလုံးသည် ဗဟိုအနေအထား၏ ကိန်းဂဏန်းဆိုင်ရာ တိုင်းတာမှုများဖြစ်သောကြောင့် ၎င်းတို့၏ အဓိပ္ပါယ်မှာ ကွဲပြားသည်။
ဆောင်းပါးတစ်ခုလုံးတွင် ရှင်းပြထားသည့်အတိုင်း၊ သင်္ချာမုဒ်သည် ဒေတာအတွဲတစ်ခုတွင် ထပ်ခါတလဲလဲ အများဆုံးတန်ဖိုးဖြစ်သည်။
ဒုတိယ၊ ဆိုလိုသည်မှာ ကိန်းဂဏန်းအချက်အလက်အားလုံး၏ ပျမ်းမျှတန်ဖိုးဖြစ်သည်။ ထို့ကြောင့်၊ အချို့သောဒေတာများ၏ ပျမ်းမျှအားရရှိရန်၊ အချက်အလက်အားလုံးကို ပေါင်းထည့်ပြီးနောက် ရလဒ်ကို လေ့လာသုံးသပ်မှုအရေအတွက်ဖြင့် ပိုင်းခြားရပါမည်။
နောက်ဆုံးအနေနှင့်၊ အလယ်အလတ်သည် ဒေတာကို အမိန့်ပေးသောအခါ ဗဟိုအနေအထားကို သိမ်းပိုက်ထားသော တန်ဖိုးဖြစ်သည်။
ထို့ကြောင့်၊ စာရင်းအင်းဆိုင်ရာတိုင်းတာမှုသုံးခုသည် ၎င်း၏ဗဟိုတန်ဖိုးများကို အိုင်ဒီယာတစ်ခုပေးသောကြောင့် ဖြစ်နိုင်ခြေဖြန့်ဝေမှုကို သတ်မှတ်ရာတွင် အထောက်အကူဖြစ်စေသည်။ သို့သော် အခြားတစ်ခုထက် သာလွန်သော အတိုင်းအတာတစ်ခုမျှ မရှိကြောင်း၊ ၎င်းတို့သည် မတူညီသော အယူအဆများကို ဆိုလိုကြောင်း သတိရပါ။
ဖက်ရှင်ကျတတ်ပါတယ်။
ဖက်ရှင်ဂုဏ်သတ္တိများမှာ-
- မုဒ်ကို အရေအတွက် ကိန်းရှင်များနှင့် အရည်အသွေးဆိုင်ရာ ကိန်းရှင်များ နှစ်မျိုးလုံးတွင် တွေ့ရှိနိုင်သည်။
- ကျွန်ုပ်တို့သည် ကျပန်းပြောင်းလဲမှုတစ်ခုသို့ မျဉ်းကြောင်းအသွင်ပြောင်းခြင်းကို အသုံးချပါက၊ အသုံးပြုသည့်လုပ်ဆောင်မှုများပေါ်မူတည်၍ ပျမ်းမျှတန်ဖိုးသည် ပြောင်းလဲသွားမည်ဖြစ်သည်။
- ယေဘုယျအားဖြင့်၊ မုဒ်သည် အစွန်းထွက်သူများအတွက် အာရုံမခံနိုင်ပါ။
- တန်ဖိုးများအားလုံးသည် ကြိမ်နှုန်းတူညီပါက၊ မုဒ်မရှိပါ။
![]()