ဆက်စပ်မက်ထရစ်
ဤဆောင်းပါးတွင် ဆက်စပ်မက်ထရစ်ဆိုသည်မှာ အဘယ်နည်း၊ ၎င်း၏ဖော်မြူလာသည် အဘယ်နည်းနှင့် ဆက်စပ်မက်ထရစ်ကို မည်သို့အနက်ပြန်ဆိုရမည်ကို သင်တွေ့ရှိပါလိမ့်မည်။ ထို့အပြင်၊ ဆက်စပ်မက်ထရစ်၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်၏ ခိုင်မာသော ဥပမာတစ်ခုကို သင်တွေ့မြင်နိုင်မည်ဖြစ်သည်။
ဆက်စပ်မက်ထရစ်ဆိုတာ ဘာလဲ။
ဆက်စပ်မက်ထရစ်သည် ကိန်းရှင် i နှင့် j ကြားရှိ ဆက်စပ်ကိန်းအမှတ် i၊j တွင်ပါရှိသော မက်ထရစ်ဖြစ်သည်။
ထို့ကြောင့်၊ ဆက်စပ်မက်ထရစ်သည် ပင်မထောင့်ဖြတ်တွင် ကိန်းဂဏာန်းများနှင့် ပြည့်စုံသော စတုရန်းမက်ထရစ်ဖြစ်ပြီး အတန်း i နှင့် ကော်လံ j ၏ဒြပ်စင်သည် ကိန်းရှင် i နှင့် ကိန်းရှင် j ကြားရှိ ဆက်စပ်ကိန်းဂဏန်းတန်ဖိုးများ ပါဝင်သည်။
ထို့ကြောင့် ဆက်စပ်မက်ထရစ်အတွက် ဖော်မြူလာ မှာ အောက်ပါအတိုင်းဖြစ်သည်။

ရွှေ
![]()
ကိန်းရှင်များကြားရှိ ဆက်စပ်ကိန်း
![]()
နှင့်
![]()
ထို့ကြောင့် ဒေတာအစုတစ်ခု၏ ဆက်စပ်မက်ထရစ်ကို ရှာဖွေရန်အတွက် ဆက်စပ်ကိန်းကို မည်ကဲ့သို့ တွက်ချက်သည်ကို သိထားရန် လိုအပ်ပါသည်။ သင်မမှတ်မိပါက၊ အောက်ပါ link တွင် online calculator ဖြင့်ပြုလုပ်နည်းကို သိရှိနိုင်မည်ဖြစ်ပါသည်။
Correlation coefficient ၏ ဂုဏ်သတ္တိမှာ ကိန်းရှင်များ၏ အစီအစဥ်သည် ၎င်း၏ တွက်ချက်မှုအတွက် အရေးမကြီးကြောင်း၊ ဆိုလိုသည်မှာ ဆက်စပ်ကိန်းများ
![]()
နှင့် ညီမျှသည်။
![]()
ထို့ကြောင့် ဆက်စပ်မက်ထရစ်သည် အချိုးကျသည်။
![Rendered by QuickLaTeX.com \displaystyle R=\begin{pmatrix}1&r_{12}&r_{13}&\dots&r_{1n}\\[1.1ex] r_{12}&1&r_{23}&\dots&r_{2n}\\[1.1ex] r_{13}&r_{23}&1&\dots&r_{3n}\\[1.1ex] \vdots &\vdots &\vdots &\ddots &\vdots\\[1.1ex] r_{1n}&r_{2n}&r_{3n}&\dots&1\end{pmatrix}](https://statorials.org/wp-content/ql-cache/quicklatex.com-76d9753ac0f42dcdc12ea4b719f37750_l3.png)
ဆက်စပ်မက်ထရစ်တစ်ခု အဓိပ္ပါယ်ရှိစေရန်အတွက်၊ ကိန်းဂဏန်းအချက်အလက်အစုတွင် ကိန်းရှင်နှစ်ခုထက်ပို၍ ရှိရပါမည်။ မဟုတ်ပါက၊ ဆက်စပ်ဆက်စပ်ကိန်းတစ်ခုအား ဆုံးဖြတ်ရန် လုံလောက်ပြီး ဆက်စပ်မက်ထရစ်သည် အဓိပ္ပာယ်ရှိမည်ဖြစ်သည်။
ဆက်စပ်မက်ထရစ်ကို ဘယ်လိုဖန်တီးမလဲ။
ဆက်စပ်မက်ထရစ်၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်အရ၊ ဤစာရင်းအင်းမက်ထရစ်အမျိုးအစားကို မည်သို့ဖန်တီးထားသည်ကို ကြည့်ကြပါစို့။
- ကိန်းရှင်တစ်စုံစီ၏ ဆက်စပ်ကိန်းကို တွက်ချက်ပါ။ ကိန်းရှင်များ၏ အစီအစဥ်သည် ရလဒ်ကို မပြောင်းလဲကြောင်း သတိပြုပါ၊ ထို့ကြောင့် ကိန်းရှင်အတွဲတစ်ခုစီအတွက် တစ်ကြိမ်သာ တွက်ချက်ရန် လိုအပ်ပါသည်။
- ဒေတာစီးရီးရှိ ကိန်းရှင်အရေအတွက်များကဲ့သို့ တူညီသောအတိုင်းအတာ၏ စတုရန်းမက်ထရစ်ကို ဖန်တီးပါ။ ဤမက်ထရစ်သည် ဆက်စပ်မက်ထရစ်ဖြစ်လိမ့်မည်။
- ဆက်စပ်မက်ထရစ်၏ ပင်မထောင့်ဖြတ်၏ အစိတ်အပိုင်းတစ်ခုစီတွင် 1 ကို ထည့်ပါ။
- ကိန်းရှင်များ၏ ဆက်စပ်ကိန်းကို i , j တို့ကို ရာထူး i , j နှင့် j , i တွင်ထည့်ပါ။
- ဆက်စပ်မက်ထရစ်ကို ဖန်တီးပြီးသည်နှင့် ကျန်အရာအားလုံးသည် ၎င်း၏တန်ဖိုးများကို အဓိပ္ပာယ်ဖွင့်ဆိုရန်ဖြစ်သည်။
ဆက်စပ်မက်ထရစ်ကို ရိုးရိုးရှင်းရှင်း လည်ပတ်ရုံဖြင့် မလုံလောက်ပါ၊ ထို့နောက် ၎င်း၏တန်ဖိုးများကို အဓိပ္ပာယ်ဖွင့်ဆိုရန်နှင့် ၎င်းတို့ကို ဆိုလိုကြောင်း နားလည်ရန် လိုအပ်ပါသည်။ အောက်ဖော်ပြပါအပိုင်းတွင် ဆက်စပ်မက်ထရစ်ကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုသည်ကို ရှင်းပြထားသည်။
ဆက်စပ် matrix ၏အဓိပ္ပာယ်ဖွင့်ဆိုချက်
ဆက်စပ်မက်ထရစ်ကို မှန်ကန်စွာအနက်ပြန်ဆိုရန်၊ ဆက်စပ်ကိန်းဂဏန်းတန်ဖိုးသည် -1 မှ +1 အထိရှိနိုင်သည်ကို ထည့်သွင်းစဉ်းစားရန် လိုအပ်ပါသည်။
- r=-1 : variable နှစ်ခုသည် ပြီးပြည့်စုံသော အနုတ်လက္ခဏာဆက်စပ်မှုရှိသည်၊ ထို့ကြောင့် အမှတ်အားလုံးချိတ်ဆက်သည့် negative slope ဖြင့်မျဉ်းကိုဆွဲနိုင်သည်။
- -1<r<0 : variable နှစ်ခုကြား ဆက်စပ်မှုသည် အနှုတ်ဖြစ်ပြီး၊ ထို့ကြောင့် ကိန်းရှင်တစ်ခု တိုးလာသောအခါ အခြားတစ်ခု လျော့နည်းသွားသည်။ တန်ဖိုးသည် -1 နှင့် ပိုနီးစပ်လေ၊ ကိန်းရှင်များသည် အနုတ်လက္ခဏာနှင့် ဆက်စပ်လေလေဖြစ်သည်။
- r=0 : variable နှစ်ခုကြား ဆက်စပ်မှုသည် အလွန်အားနည်းသည်၊ တကယ်တော့ ၎င်းတို့ကြားရှိ linear ဆက်ဆံရေးသည် သုညဖြစ်သည်။ ၎င်းသည် ကိန်းရှင်များသည် အမှီအခိုကင်းသည်ဟု မဆိုလိုပါ၊ ၎င်းတို့သည် လိုင်းမဟုတ်သော ဆက်ဆံရေးရှိနိုင်သောကြောင့်ဖြစ်သည်။
- 0<r<1 : ကိန်းရှင်နှစ်ခုကြား ဆက်စပ်မှုသည် အပြုသဘောဖြစ်ပြီး၊ တန်ဖိုးသည် +1 နှင့် ပိုနီးစပ်လေ၊ ကိန်းရှင်များကြား ဆက်ဆံရေး အားကောင်းလေဖြစ်သည်။ ဤကိစ္စတွင်၊ အခြားတစ်ခုသည် တိုးလာသောအခါတွင် ကိန်းရှင်တစ်ခုသည် ၎င်း၏တန်ဖိုးကို တိုးတတ်ပါသည်။
- r=1 : ကိန်းရှင်နှစ်ခုသည် ပြီးပြည့်စုံသော အပြုသဘောဆက်စပ်ဆက်စပ်မှုရှိသည်၊ ဆိုလိုသည်မှာ ၎င်းတို့သည် အပြုသဘောဆောင်သောမျဉ်းကြောင်းဆိုင်ရာ ဆက်နွယ်မှုရှိသည်။
ထို့ကြောင့် ဆက်စပ်မက်ထရစ်ကို အဓိပ္ပာယ်ဖွင့်ဆိုရန်၊ ဆက်စပ်ကိန်းတစ်ခုစီကို အနက်ဖွင့်ပြီး မတူညီသောရလဒ်များကို နှိုင်းယှဉ်ရန် လိုအပ်သည်။
ဤနည်းဖြင့် မည်သည့် variables များသည် တစ်ခုနှင့်တစ်ခု ဆက်စပ်မှုအရှိဆုံးဖြစ်သည်၊ မည်သည့် variables များသည် အရေးကြီးဆုံးဖြစ်သည်၊ မည်သည့် variables များသည် လက်တွေ့ကျကျတွင် တစ်ခုနှင့်တစ်ခု ဆက်စပ်မှုမရှိသည်ကို သိနိုင်မည်ဖြစ်သည်။
Correlation Matrix ဥပမာ
ဆက်စပ် matrix တွင် အဘယ်အရာပါဝင်ပြီး ၎င်းကို အဓိပ္ပာယ်ဖွင့်ဆိုသည်ကို အပြည့်အဝနားလည်ရန်၊ ဤအပိုင်းတွင် ဆက်စပ်မက်ထရစ်တစ်ခု၏ ဥပမာတစ်ခုကို ပိုင်းခြားစိတ်ဖြာပါမည်။
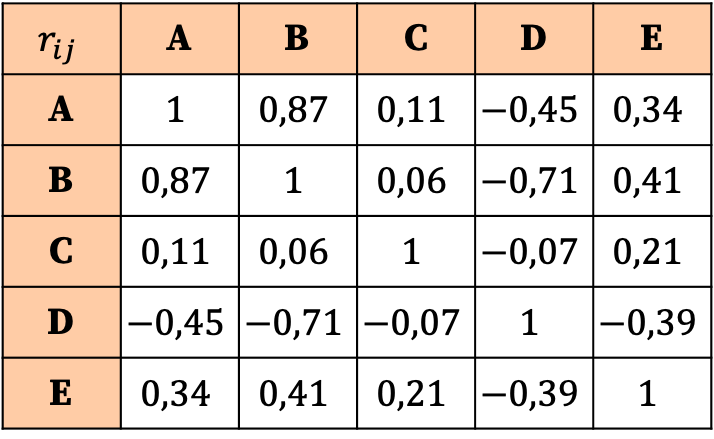
ဆက်စပ်မက်ထရစ်၏ အဓိပ္ပာယ်ဖွင့်ဆိုချက်သည် ဖော်ကိန်းများ၏ တန်ဖိုးများပေါ်တွင် အခြေခံသည်။ ထို့ကြောင့်၊ ၎င်း၏ဆက်စပ်ဖော်ကိန်းသည် အကြီးဆုံး (0.87) ဖြစ်သောကြောင့် အပြင်းထန်ဆုံးသောဆက်စပ်ဆက်နွယ်မှုသည် ကိန်းရှင် A နှင့် ကိန်းရှင် B အကြားဆက်နွယ်မှုဖြစ်သည်ကို ကျွန်ုပ်တို့တွေ့နိုင်သည်။
အခြားတစ်ဖက်တွင်၊ variable C သည် မည်သည့် variable နှင့်မဆို ဆက်စပ်မှုမရှိပေ။ ထို့ကြောင့်၊ ခွဲခြမ်းစိတ်ဖြာမှုကို ရိုးရှင်းစေရန်၊ ဤကိန်းရှင်ကို ကိန်းဂဏန်းလေ့လာမှုမှ ဖယ်ရှားရန်ပင် စဉ်းစားနိုင်သည်။
အလားတူ၊ variable D နှင့် အခြားသော variables များ၏ ဆက်ဆံရေးအားလုံးသည် အနုတ်လက္ခဏာဖြစ်သည်၊ ဆိုလိုသည်မှာ variable D နှင့် အခြားသော variable များကြား ဆက်စပ်မှုသည် ပြောင်းပြန်ဖြစ်သည်။ variable D သည် အနှုတ်လက္ခဏာနှင့် ဆက်နွယ်နေရုံမျှဖြင့် ကိန်းရှင်ကို ဖယ်ရှားသင့်သည်ဟု မဆိုလိုပါ။
သင်တွေ့မြင်ရသည့်အတိုင်း၊ ဆက်စပ်မက်ထရစ်သည် ဒေတာအကျဉ်းချုပ်နှင့် ဒေတာအတွဲရှိ မတူညီသောကိန်းရှင်များကြားရှိ ဆက်စပ်မှုကို အလုံးစုံခွဲခြမ်းစိတ်ဖြာမှုပြုလုပ်ရန်အတွက် အလွန်အသုံးဝင်ပါသည်။