ဆုတ်ယုတ်မှုမျဉ်း

အားဖြင့် Benjamin Anderson ဩဂုတ် 2, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးသည် စာရင်းဇယားများတွင် ဆုတ်ယုတ်မှုမျဉ်းကြောင်းကို ရှင်းပြထားသည်။ ထို့ကြောင့်၊ ကိန်းရှင်နှစ်ခုကြားရှိ ဆုတ်ယုတ်မှုမျဉ်းကို တွက်ချက်နည်း၊ ဖြေရှင်းထားသော လေ့ကျင့်ခန်းတစ်ခုနှင့် ဒေတာနမူနာများအတွက် ဆုတ်ယုတ်မှုမျဉ်းကို တွက်ချက်ရန် အွန်လိုင်းဂဏန်းတွက်စက်ကို သင်တွေ့လိမ့်မည်။

ဆုတ်ယုတ်မှုမျဉ်းက ဘာလဲ။

စာရင်းဇယားများတွင်၊ ဆုတ်ယုတ်မှုမျဉ်း သည် ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုပုံစံ မှရရှိသောမျဉ်းဖြစ်သည်။ ပို၍တိကျသည်မှာ၊ ဆုတ်ယုတ်မှုမျဉ်းသည် ဖြန့်ကြဲကွက်တစ်ခုအတွက် အသင့်တော်ဆုံးမျဉ်းဖြစ်ပြီး ထို့ကြောင့် ကိန်းဂဏန်းအချက်အလက်အစုအဝေးကို အကောင်းဆုံးဖော်ပြသည်။

ထို့ကြောင့်၊ regression line equation သည် သင်္ချာအားဖြင့် သီးခြားကိန်းရှင် X နှင့် data set တစ်ခု၏ မှီခို variable Y ကို ဆက်စပ်ပေးပါသည်။ ဆုတ်ယုတ်မှုမျဉ်းသည် ယေဘုယျအားဖြင့် ရှုမြင်မှုတစ်ခုစီ၏တန်ဖိုးကို တိကျစွာဆုံးဖြတ်နိုင်စွမ်းမရှိသော်လည်း၊ ၎င်းသည် ၎င်း၏တန်ဖိုးကို အနီးစပ်ဆုံးဖော်ပြနိုင်သည်။

ယခင်ဂရပ်တွင် သင်တွေ့မြင်ရသည့်အတိုင်း၊ ဆုတ်ယုတ်မှုမျဉ်းသည် ကျွန်ုပ်တို့အား ဒေတာအစုတစ်ခု၏ လမ်းကြောင်းသစ်နှင့် အမှီအခိုကင်းသော ကိန်းရှင်နှင့် အမှီအခိုကင်းသော ကိန်းရှင်ကြားရှိ ဆက်ဆံရေးအမျိုးအစားကို မြင်နိုင်ရန် ကူညီပေးသည်။ အောက်တွင်ကျွန်ုပ်တို့သည် regression line ၏ applications များကိုကြည့်ရှုပါမည်။

Regression line ဖော်မြူလာ

ဆုတ်ယုတ်မှုမျဉ်း၏အဓိပ္ပါယ်ကို ယခုကျွန်ုပ်တို့သိပြီးသောအခါ၊ linear regression model ၏မျဉ်း၏ညီမျှခြင်းအား တွက်ချက်နည်းကိုကြည့်ကြပါစို့။

မည်သည့်မျဉ်းကဲ့သို့ပင်၊ ဆုတ်ယုတ်မှုမျဉ်း၏ ညီမျှခြင်းကို ကိန်းသေ (b ₀ ) နှင့် လျှောစောက် (b ₁ ) ဖြင့် ဖွဲ့စည်းထားသည်။

$y=b_0+b_1x$

ထို့ကြောင့် linear regression line ၏ coefficients များကို တွက်ချက်ရန် ဖော်မြူလာများမှာ အောက်ပါအတိုင်းဖြစ်သည် ။

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[12ex]b_0=\overline{y}-b_1\overline{x}\end{array}$

ရွှေ-

$b_0$

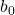
regression line ၏ ကိန်းသေဖြစ်ပါသည်။
$b_1$

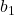
regression line ၏ slope ဖြစ်သည်။
$x_i$

ဒေတာ i ၏ လွတ်လပ်သော ကိန်းရှင် X ၏ တန်ဖိုးဖြစ်သည်။
$y_i$

ဒေတာ i ၏ မှီခို variable Y ၏ တန်ဖိုးဖြစ်သည်။
$\overline{x}$

လွတ်လပ်သော variable ၏ပျမ်းမျှတန်ဖိုးများဖြစ်သည်။
$\overline{y}$

dependent variable Y ၏ ပျမ်းမျှတန်ဖိုးများဖြစ်သည်။

👉 မည်သည့်ဒေတာအစုံအတွက်မဆို regression line ကိုတွက်ချက်ရန် အောက်ပါ calculator ကိုသုံးနိုင်သည်။

ဆုတ်ယုတ်မှုမျဉ်း၏ ခိုင်မာသော ဥပမာ

ဆုတ်ယုတ်မှုမျဉ်း၏ သဘောတရားကို ထပ်မံလေ့လာရန်၊ အောက်ဖော်ပြပါသည် ဆုတ်ယုတ်မှုမျဉ်းကို ဖန်တီးပုံ၏ လုပ်ဆောင်ခဲ့သော ဥပမာတစ်ခုဖြစ်သည်။

စာရင်းအင်း စာမေးပွဲကိုဖြေဆိုပြီးနောက် ကျောင်းသားငါးဦးအား စာမေးပွဲတွင် မည်မျှကြာအောင် သင်ကြားခဲ့သည်ကို မေးမြန်းခဲ့ရာ ဒေတာကို အောက်ပါဇယားတွင် ပြထားသည်။ ရရှိသော အတန်းနှင့် စာသင်ချိန်များကို မျဉ်းသားစွာ ဆက်စပ်နိုင်ရန် စုဆောင်းထားသော ကိန်းဂဏန်း အချက်အလက်မှ ဆုတ်ယုတ်မှုမျဉ်းကို တွက်ချက်ပါ။ ထို့နောက် 8 နာရီစာလေ့လာသော ကျောင်းသားသည် မည်သည့်တန်းကို ဖြေဆိုရမည်ကို ဆုံးဖြတ်ပါ။

နမူနာဒေတာအတွက် ဆုတ်ယုတ်မှုမျဉ်းကိုရှာရန်၊ ကျွန်ုပ်တို့သည် ညီမျှခြင်း၏ coefficients b ₀ နှင့် b ₁ ကိုဆုံးဖြတ်ရန် လိုအပ်ပြီး ထိုသို့ပြုလုပ်ရန်အတွက်၊ ကျွန်ုပ်တို့သည် အထက်အပိုင်းတွင်တွေ့ရသော ဖော်မြူလာများကို အသုံးပြုရန်လိုအပ်ပါသည်။

သို့သော်၊ linear regression line အတွက် ဖော်မြူလာများကို အသုံးချရန်၊ အမှီအခိုကင်းသော variable ၏ ဆိုလိုချက်နှင့် dependent variable ၏ mean ကို ဦးစွာ တွက်ချက်ရပါမည်။

$\begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}$

ယခု ကျွန်ုပ်တို့သည် ကိန်းရှင်များ၏ အဓိပ္ပါယ်ကို သိရှိပြီး၊ ကျွန်ုပ်တို့သည် သက်ဆိုင်ရာ ဖော်မြူလာကို အသုံးပြု၍ မော်ဒယ်၏ ဖော်မြူကိန်း b ₁ ကို တွက်ချက်သည်-

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}$

နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် သက်ဆိုင်ရာ ဖော်မြူလာကို အသုံးပြု၍ မော်ဒယ်၏ ကိန်းဂဏန်း b ₀ ကို တွက်ချက်သည်-

$\begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}$

အတိုချုပ်အားဖြင့်၊ ပြဿနာ၏ linear regression line ၏ ညီမျှခြင်းမှာ အောက်ပါအတိုင်းဖြစ်သည် ။

$y=2,0294+0,4412x$

အောက်တွင် နမူနာဒေတာ၏ ဂရပ်ဖစ်ကိုယ်စားပြုမှုအပြင် ရိုးရှင်းသော linear regression model ၏ မျဉ်းဖြောင့်ကို သင်တွေ့မြင်နိုင်သည်-

ဆုတ်ယုတ်မှုမျဉ်းကို ကျွန်ုပ်တို့ တွက်ချက်ပြီးသည်နှင့် ၈ နာရီကြာ လေ့လာသော ကျောင်းသားတစ်ဦး ရရှိမည့် အတန်းကို ခန့်မှန်းရန်၊ ရရှိသော ဆုတ်ယုတ်မှုမျဉ်း၏ ညီမျှခြင်းတွင် ဤတန်ဖိုးကို အစားထိုးပါ။

$y=2,0294+0,4412\cdot 8=5,56$

ထို့ကြောင့် ကျောင်းသားတစ်ဦးသည် ရှစ်နာရီကြာ လေ့လာပါက စာမေးပွဲတွင် ရမှတ် 5.56 ရရှိမည်ဖြစ်သည်။

ဆုတ်ယုတ်မှုမျဉ်းကို ဘာအတွက်အသုံးပြုသလဲ။

အဓိကအားဖြင့်၊ regression line တွင် အသုံးပြုမှု နှစ်ခုရှိသည်- regression line ကို variable နှစ်ခုကြားရှိ ဆက်စပ်မှု အမျိုးအစားကို ဆုံးဖြတ်ရန် အသုံးပြုပြီး အခြားတစ်ဖက်တွင်၊ regression line သည် စူးစမ်းမှုအသစ်တစ်ခု၏ တန်ဖိုးကို ခန့်မှန်းနိုင်စေပါသည်။

ဆုတ်ယုတ်မှုမျဉ်း၏ လျှောစောက်သည် အမှီအခိုကင်းသော ကိန်းရှင်နှင့် မှီခိုကိန်းရှင်တို့၏ ဆက်စပ်ပုံ ကို ပြောပြသည်။ slope သည် positive ဖြစ်ပါက၊ dependent variable သည် သီးခြား variable နှင့် တိုက်ရိုက်အချိုးကျသည်ဟု ဆိုလိုပြီး slope သည် negative ဖြစ်ပါက၊ variable များသည် ပြောင်းပြန်အချိုးကျသည်ဟု ဆိုလိုသည်။ နောက်ဆုံးတွင်၊ slope coefficient သည် သုညနှင့် အလွန်နီးစပ်ပါက၊ ဆိုလိုသည်မှာ ကိန်းရှင်နှစ်ခုကြားရှိ ဆက်စပ်မှုသည် အလွန်အားနည်းပါသည်။

ထို့အပြင်၊ regression line ၏ equation ကို သိရှိပါက၊ အထက်ဖော်ပြပါ ဥပမာတွင် ကျွန်ုပ်တို့ပြုခဲ့သည့်အတိုင်း သီးခြား variable ၏ တန်ဖိုးအသစ်အတွက် dependent variable ၏တန်ဖိုးကို ခန့်မှန်းနိုင်ပါသည်။ ထို့ကြောင့် ဆုတ်ယုတ်မှုမျဉ်းကို ပိုမိုကောင်းမွန်စွာ လိုက်လျောညီထွေဖြစ်အောင် ပြုလုပ်လေလေ၊ ကြိုတင်ခန့်မှန်းမှုများ ပိုကောင်းလေဖြစ်သည်။

ဆုတ်ယုတ်မှုမျဉ်းဂဏန်းတွက်စက်

ကိန်းရှင်နှစ်ခုကြားရှိ ဆုတ်ယုတ်မှုမျဉ်းကို တွက်ချက်ရန် အောက်ပါဂဏန်းပေါင်းစက်ထဲသို့ ဒေတာနမူနာတစ်ခုကို ထည့်သွင်းပါ။ သင်သည် ဒေတာအတွဲများကို ခွဲခြားထားရန် လိုအပ်သည်၊ ထို့ကြောင့် ပထမအကွက်တွင် အမှီအခိုကင်းသော ကိန်းရှင် X ၏ တန်ဖိုးများသာ ရှိပြီး ဒုတိယအကွက်တွင် မှီခိုနေသော ကိန်းရှင် Y ၏ တန်ဖိုးများသာ ရှိနေမည်ဖြစ်သည်။

ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။