တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်း

ဤဆောင်းပါးသည် ကိန်းဂဏန်းစာရင်းအင်းများတွင် တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းကို ရှင်းပြထားသည်။ ထို့ကြောင့်၊ တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်း၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်၊ တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းကို မည်သို့ရရှိနိုင်ပုံနှင့် လေ့ကျင့်ခန်းနှစ်ခုကို တစ်ဆင့်ပြီးတစ်ဆင့် ဖြေရှင်းနိုင်သည်ကို သင်တွေ့လိမ့်မည်။

တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းဆိုသည်မှာ အဘယ်နည်း။

ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ ပွားများသော နှိုင်းရကြိမ်နှုန်း သည် ဆွေမျိုးကြိမ်နှုန်းများ၏ စုစည်းပေါင်းလဒ်ဖြစ်သည်။ ဆိုလိုသည်မှာ၊ တန်ဖိုးတစ်ခု၏ တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းသည် ထိုတန်ဖိုး၏ နှိုင်းရကြိမ်နှုန်းနှင့် ၎င်းထက်နည်းသော တန်ဖိုးအားလုံး၏ ဆွေမျိုးကြိမ်နှုန်းများနှင့် ညီမျှသည်။

တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းအတွက် သင်္ကေတမှာ H _i ဖြစ်သည်။ သို့သော်လည်း စာရင်းဇယားများတွင် ဤကြိမ်နှုန်းအမျိုးအစားအတွက် သင်္ကေတနှင့် ပတ်သက်၍ ပြီးပြည့်စုံသော သဘောတူညီမှု မရရှိသေးသောကြောင့် ၎င်းကို အခြားသင်္ကေတကို အသုံးပြု၍ ဖော်ပြသည်ကို သင်တွေ့နိုင်သည်။

သိသာထင်ရှားစွာ၊ တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်း၏ အဓိပ္ပါယ်ကို နားလည်ရန်၊ နှိုင်းယှဥ်ကြိမ်နှုန်း၏ သဘောတရားကို ဦးစွာ ရှင်းရှင်းလင်းလင်း သိထားရမည်ဖြစ်ပြီး၊ ထို့ကြောင့် ရှင်းလင်းချက်မပြမီ အောက်ပါလင့်ခ်ကို ဝင်ကြည့်ရန် အကြံပြုလိုပါသည်-

တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းကို တွက်ချက်နည်း

တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းကို တွက်ချက်ရန်၊ အောက်ပါအဆင့်များကို လိုက်နာရပါမည်-

1. ကိန်းဂဏန်းနမူနာမှ မတူညီသောတန်ဖိုးများအားလုံးကို ကြိမ်နှုန်းဇယားတစ်ခုတည်ဆောက်ပါ။
2. တန်ဖိုးတစ်ခုစီ၏ ပကတိကြိမ်နှုန်းကို တွက်ချက်ပါ။
3. အကြွင်းမဲ့ ကြိမ်နှုန်းများမှ၊ တန်ဖိုးတစ်ခုစီ၏ နှိုင်းရကြိမ်နှုန်းကို ဆုံးဖြတ်ပါ။
4. တန်ဖိုးတစ်ခုစီ၏ နှိုင်းရကြိမ်နှုန်းကို ပေါင်းထည့်ခြင်းဖြင့် တွက်ချက်ထားသည့် တန်ဖိုးတစ်ခုစီ၏ နှိုင်းယှဥ်ကြိမ်နှုန်းကို ရှာပါ။

တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်း ရာခိုင်နှုန်းကို တွက်ချက်လိုပါက ရာခိုင်နှုန်းအဖြစ် ဖော်ပြသည့် တိုးပွားလာသော ဆွေမျိုးကြိမ်နှုန်းကို တွက်ချက်လိုပါက တူညီသောအဆင့်များကို လိုက်နာပြီး ရလဒ်များကို 100 ဖြင့် မြှောက်ရန် လိုအပ်ကြောင်း မှတ်သားထားပါ။

စုပေါင်းနှိုင်းရကြိမ်နှုန်း ဥပမာများ

တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းကို မည်ကဲ့သို့ တွက်ချက်သည်ကို သင်မြင်နိုင်စေရန်၊ ဖြေရှင်းထားသော ဥပမာနှစ်ခုကို အောက်တွင်ဖော်ပြထားသည်။ ပထမဥပမာတွင်၊ လုပ်ငန်းစဉ်အနည်းငယ်ကွဲပြားသောကြောင့်၊ ဒုတိယဥပမာတွင်၊ စဉ်ဆက်မပြတ်ကိန်းရှင်တစ်ခု၏ ဆက်စပ်ကြိမ်နှုန်းကို ကျွန်ုပ်တို့တွေ့ရှိသည်။

ဥပမာ 1- အဆက်မပြတ်ပြောင်းလဲနိုင်သော

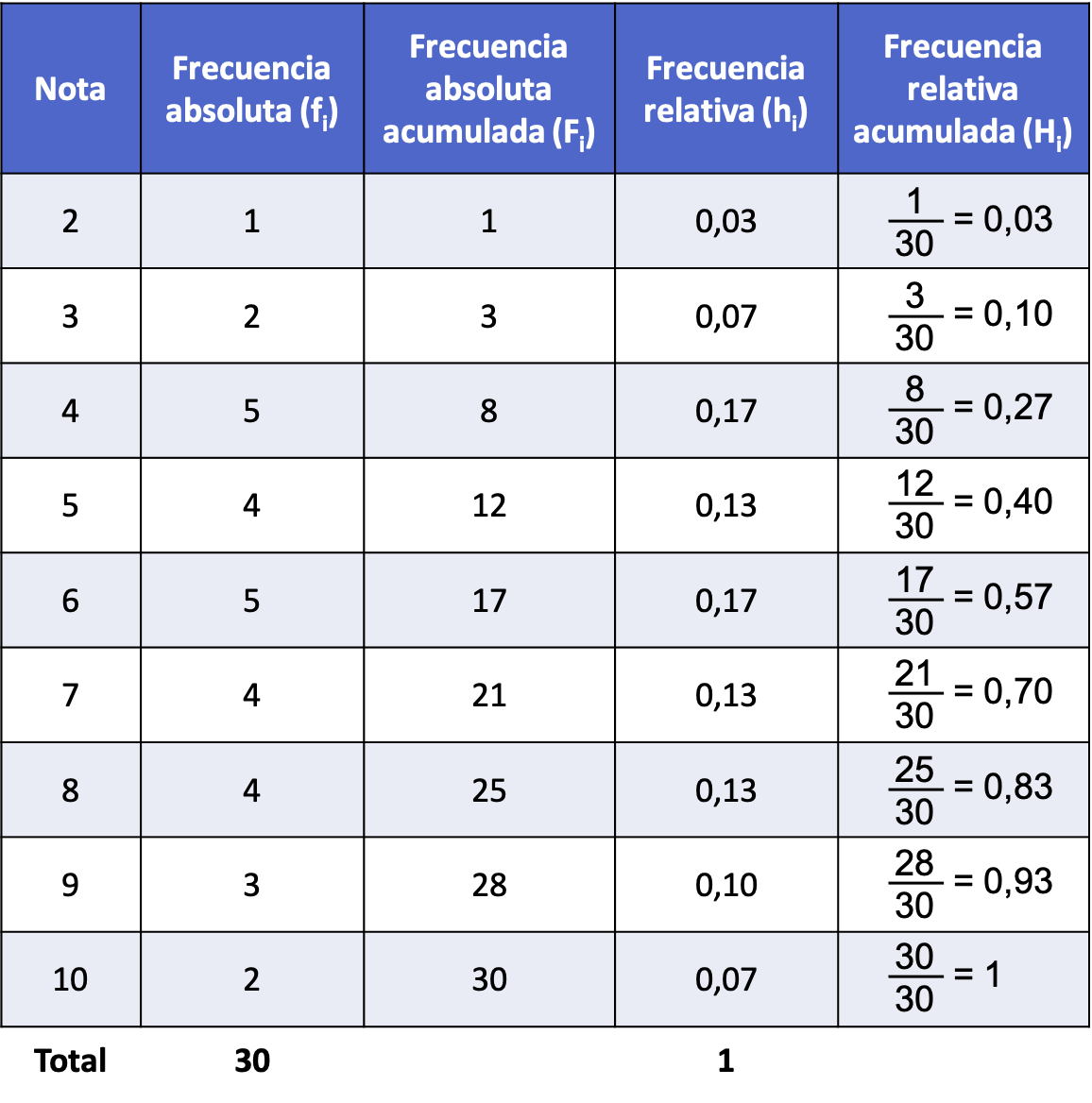
• ကျောင်းသား 30 ရှိသော အတန်းတစ်တန်းတွင် စာရင်းအင်းဘာသာရပ်တွင် ရရှိသော အမှတ်များမှာ အောက်ပါအတိုင်းဖြစ်သည်။ မှတ်စုတစ်ခုစီ၏ တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းသည် အဘယ်နည်း။

ဤကိစ္စတွင်၊ ကိန်းရှင်သည် ဒဿမတန်ဖိုးကိုမယူနိုင်သောကြောင့် ကွဲပြားသည်။ ထို့ကြောင့် ဒေတာများကို ကြားကာလအလိုက် အုပ်စုဖွဲ့ရန် မလိုအပ်သော်လည်း တွက်ချက်မှုများကို တိုက်ရိုက်လုပ်ဆောင်နိုင်သည်။

ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် ကြိမ်နှုန်းဇယားကိုရေးဆွဲပြီး မတူညီသောတန်ဖိုးတစ်ခုစီ၏ ပကတိကြိမ်နှုန်းကို ဆုံးဖြတ်သည်-

ထို့နောက်၊ ကျွန်ုပ်တို့သည် တန်ဖိုးတစ်ခုစီ၏ နှိုင်းရကြိမ်နှုန်းကို တွက်ချက်သည် (ဤအရာကို ပို့စ်၏အစတွင် လင့်ခ်တွင် သင်ကြည့်ရှုနိုင်သည်)။

ပြီးတော့ dataset ရဲ့ absolute frequency နဲ့ relative frequency ကို တွက်ချက်ပြီးတာနဲ့၊ cumulative relative frequency ကို ရနိုင်ပါတယ်။ ၎င်းကိုလုပ်ဆောင်ရန်၊ မေးခွန်းရှိတန်ဖိုး၏ နှိုင်းရကြိမ်နှုန်းနှင့် ယခင်နှိုင်းရကြိမ်နှုန်းများအားလုံးကို ပေါင်းထည့်ရမည် သို့မဟုတ် တစ်နည်းဆိုရသော် ယခင်စုဆောင်းထားသော နှိုင်းရကြိမ်နှုန်းကို ပေါင်းထည့်ရပါမည်။

အတိုချုပ်အားဖြင့်၊ absolute frequency၊ relative frequency နှင့် cumulative relative frequency ပါရှိသော ကြိမ်နှုန်းဇယားမှာ အောက်ပါအတိုင်းဖြစ်သည် ။

တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်း၏ နောက်ဆုံးတန်ဖိုးသည် အမြဲတမ်း 1 ဖြစ်သင့်သည်။ အခြားနံပါတ်ရပါက၊ တွက်ချက်မှုတွင် သင်သည် မှားယွင်းသွားသည်ဟု ဆိုလိုသည်။

ဥပမာ 2- စဉ်ဆက်မပြတ်ကိန်းရှင်

• လူ 20 ၏အမြင့်ကိုတိုင်းတာခဲ့ပြီးအောက်ပါရလဒ်များကိုရရှိခဲ့သည်။ ဒေတာကို ကြားကာလများအဖြစ် ပိုင်းခြားပြီး ကြားကာလတစ်ခုစီ၏ တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းကို ရှာပါ။

ကိန်းဂဏန်းများသည် ဒဿမဖြစ်သောကြောင့် ဤကိစ္စရပ်သည် ယခင်ပြဿနာနှင့် ကွဲပြားသည်၊ ဆိုလိုသည်မှာ ကိန်းရှင်သည် မည်သည့်တန်ဖိုးကိုမဆို ယူနိုင်ပြီး ထို့ကြောင့် ဆက်တိုက်ဖြစ်နေသည်။ ထို့ကြောင့် ဒေတာများကို ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ခြင်းဖြင့် ကြိမ်နှုန်းဇယားကို ဖန်တီးပါမည်။

ထို့ကြောင့် ကျွန်ုပ်တို့သည် ဇယားကိုတည်ဆောက်ပြီး ကြားကာလတစ်ခုစီ၏ ပကတိကြိမ်နှုန်းကို ရယူသည်-

ယခု ကျွန်ုပ်တို့သည် ကြားကာလတစ်ခုစီ၏ ပကတိကြိမ်နှုန်းကို ဒေတာအမှတ်စုစုပေါင်းဖြင့် ပိုင်းခြားခြင်းဖြင့် နှိုင်းရကြိမ်နှုန်းများကို တွက်ချက်ပါသည်။

နောက်ဆုံးတွင်၊ ကြားကာလအားလုံး၏ တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းများကို ကျွန်ုပ်တို့ ရှာတွေ့သည်။ ယခင်ကအတိုင်း၊ ကြားကာလတစ်ခု၏ တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းကို ဆုံးဖြတ်ရန်အတွက် ၎င်းကြားကာလ၏ နှိုင်းရကြိမ်နှုန်းနှင့် ယခင်ဆွေမျိုးကြိမ်နှုန်းများကို ပေါင်းထည့်ရန် လိုအပ်သည်-

တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းနှင့် စုစည်းမှု အကြွင်းမဲ့ အကြိမ်ရေ

နှိုင်းယှဥ်ကြိမ်နှုန်းမှ တိုးပွားလာသော နှိုင်းယှဥ်ကြိမ်နှုန်းကို မည်ကဲ့သို့ ဆင်းသက်လာသည်ကို ကျွန်ုပ်တို့ မြင်လိုက်ရပါသည်။ သို့သော်၊ ဤကြိမ်နှုန်းအမျိုးအစားကို စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်းကို အသုံးပြု၍လည်း တွေ့ရှိနိုင်သည်။

နမူနာရှိ ဒေတာစုစုပေါင်းအရေအတွက်ဖြင့် စုစည်း ဆက်စပ် ကြိမ်နှုန်းကို တွက်ချက်နိုင်သည်။

ထို့ကြောင့်၊ တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းအတွက် ဖော်မြူလာ မှာ-

ရွှေ-

• 

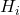
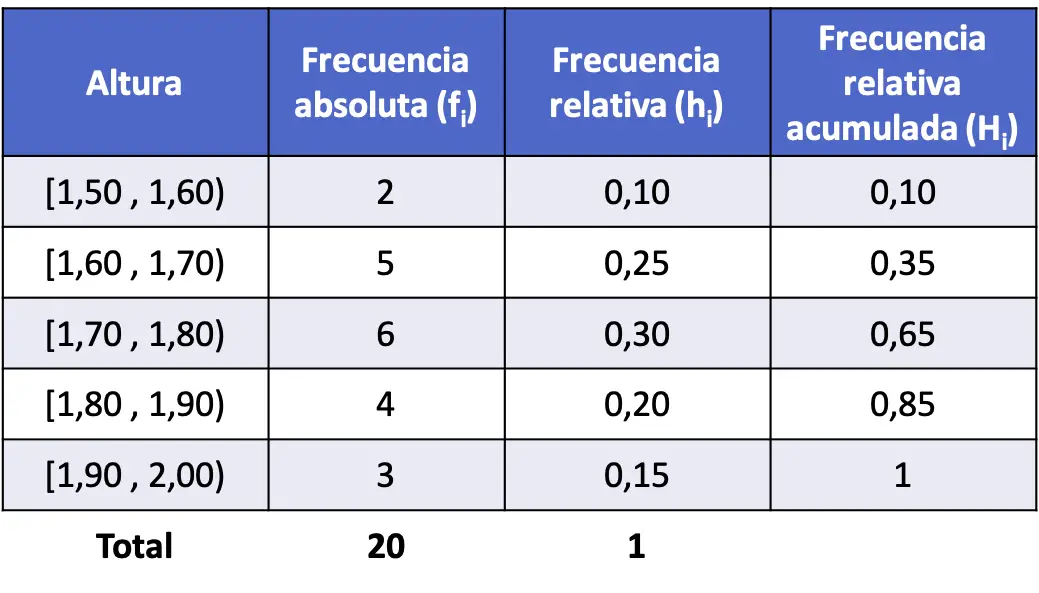
  တိုးပွားလာသော နှိုင်းရကြိမ်နှုန်းဖြစ်သည်။

• 

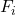
  စုဆောင်းထားသော absolute frequency ဖြစ်သည် ။

• 

  ဒေတာစုစုပေါင်းအရေအတွက်ဖြစ်သည်။

အထက်ဖော်ပြပါ ပထမဥပမာကို အကောင်အထည်ဖော်ပြီးနောက်၊ ဤနေရာတွင် စုစည်းထားသော နှိုင်းရကြိမ်နှုန်းကို စုဆောင်းထားသော absolute frequency မှ မည်သို့တွေ့ရှိနိုင်သည်-

အထက်ဖော်ပြပါဇယားကို ၎င်းတွင် ကိန်းဂဏန်းဆိုင်ရာ ကြိမ်နှုန်းများ အမျိုးအစားအားလုံးပါ၀င်သောကြောင့်၊ ကြိမ်နှုန်းဇယားဟုခေါ်သည်။ ပိုမိုသိရှိရန် ဤနေရာကိုနှိပ်ပါ-