Ridge regression နိဒါန်း

သာမာန် မျဉ်းကြောင်းမျိုးစုံဆုတ်ယုတ်မှု တွင်၊ ကျွန်ုပ်တို့သည် ပုံစံတစ်ခု၏မော်ဒယ်နှင့်ကိုက်ညီရန် p ကြိုတင်ခန့်မှန်းကိန်းရှင် ကိန်းရှင်များနှင့် တုံ့ပြန်မှုကိန်းရှင် တစ်ခုကို အသုံးပြုသည်-

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

ရွှေ-

• Y : တုံ့ပြန်မှု ကိန်းရှင်
• X _j : j ^th ကြိုတင်ခန့်မှန်းနိုင်သောကိန်းရှင်
• β _j : X _j တွင် တစ်ယူနစ်တိုးလာမှု၏ Y ပေါ်ရှိ ပျမ်းမျှအကျိုးသက်ရောက်မှုသည် အခြားကြိုတင်ခန့်မှန်းသူအားလုံးကို ပုံသေသတ်မှတ်ထားသည်
• ε : အမှားအယွင်း ကိန်း

β ₀ , β ₁ , B ₂ , …, β _p ၏ တန်ဖိုးများကို အကြွင်းအကျန်များ (RSS) ၏ နှစ်ထပ်ကိန်းများကို အနည်းဆုံးဖြစ်စေသည့် အနည်းဆုံး စတုရန်းပုံနည်းလမ်းကို အသုံးပြု၍ ရွေးချယ်ထားသည်။

RSS = Σ(y _i – ŷ _i ) ^၂

ရွှေ-

• ∑ : ပေါင်းလဒ် ဟု အဓိပ္ပာယ်ရသော ဂရိသင်္ကေတ
• y _i : ^{အိုင်တီ} လေ့လာခြင်းအတွက် အမှန်တကယ် တုံ့ပြန်မှုတန်ဖိုး
• ŷ _i : Multiple linear regression model ကို အခြေခံ၍ ခန့်မှန်းထားသော တုံ့ပြန်မှုတန်ဖိုး

သို့ရာတွင်၊ ကြိုတင်ခန့်မှန်းနိုင်သောကိန်းရှင်များသည် အလွန်ဆက်စပ်နေသောအခါတွင်၊ ကော်လိုင်းပေါင်းစုံသည် ပြဿနာဖြစ်လာနိုင်သည်။ ၎င်းသည် မော်ဒယ်ဖော်ကိန်း ခန့်မှန်းချက်များကို ယုံကြည်စိတ်ချမှုမရှိစေဘဲ ကွဲပြားမှုမြင့်မားမှုကို ပြသနိုင်သည်။

ဤပြဿနာကို ပြေလည်အောင်ဖြေရှင်းရန် နည်းလမ်းတစ်ခုမှာ မော်ဒယ်မှ ခန့်မှန်းပေးသူ variable များကို လုံးဝဖယ်ရှားခြင်းမရှိဘဲ အောက်ပါတို့ကို လျှော့ချရန် ရှာဖွေသည့် ridge regression ဟုခေါ်သော နည်းလမ်းကို အသုံးပြုခြင်းဖြစ်သည်-

RSS + λΣβ _j ^၂

j သည် 1 မှ p နှင့် λ ≥ 0 ရှိရာ။

ညီမျှခြင်းတွင် ဤဒုတိယအခေါ်အဝေါ်ကို ရုပ်သိမ်းပြစ်ဒဏ် ဟု ခေါ်သည်။

λ = 0 ဖြစ်သောအခါ၊ ဤပြစ်ဒဏ်အသုံးအနှုန်းသည် အကျိုးသက်ရောက်မှုမရှိပါ၊ ခေါင်ဆုတ်ဆုတ်ခြင်းသည် တူညီသောကိန်းဂဏန်းခန့်မှန်းချက်ကို အနည်းဆုံးစတုရန်းအဖြစ်ထုတ်ပေးသည်။ သို့သော်လည်း၊ λ သည် အဆုံးမရှိ ချဉ်းကပ်လာသည်နှင့်အမျှ၊ ကျုံ့သွားသော ပြစ်ဒဏ်သည် ပို၍ သြဇာကြီးမားလာပြီး အမြင့်ဆုံး ဆုတ်ယုတ်မှုကိန်းဂဏန်း ခန့်မှန်းချက်သည် သုညသို့ ချဉ်းကပ်လာသည်။

ယေဘူယျအားဖြင့်၊ မော်ဒယ်ရှိ သြဇာအနည်းဆုံး ခန့်မှန်းနိုင်သော ကိန်းရှင်များသည် အမြန်ဆုံး သုညဆီသို့ ကျဆင်းသွားပါမည်။

Ridge Regression ကို ဘာကြောင့် သုံးတာလဲ။

Ridge regression သည် အနည်းဆုံး စတုရန်းများ ဆုတ်ယုတ်ခြင်းထက် အားသာချက်မှာ bias-variance tradeoff ဖြစ်သည်။

Mean Square Error (MSE) သည် ပေးထားသော မော်ဒယ်တစ်ခု၏ တိကျမှုကို တိုင်းတာရန် အသုံးပြုနိုင်သည့် မက်ထရစ်တစ်ခုဖြစ်ပြီး ၎င်းကို အောက်ပါအတိုင်း တွက်ချက်ထားသည်-

MSE = Var( f̂( x ₀ )) + [Bias( f̂( x ₀ ))] ² + Var(ε)

MSE = Variance + Bias ² + Irreducible အမှား

Ridge regression ၏ အခြေခံအယူအဆမှာ ကွဲလွဲမှုကို သိသာထင်ရှားစွာ လျှော့ချနိုင်ပြီး အလုံးစုံ MSE ကို နိမ့်ကျစေရန် သေးငယ်သော ဘက်လိုက်မှုကို မိတ်ဆက်ရန်ဖြစ်သည်။

ယင်းကို သရုပ်ဖော်ရန် အောက်ပါဂရပ်ကို သုံးသပ်ပါ။

λ တိုးလာသည်နှင့်အမျှ ဘက်လိုက်မှု အနည်းငယ်တိုးလာသဖြင့် ကွဲလွဲမှု သိသိသာသာ လျော့ကျသွားသည်ကို သတိပြုပါ။ သို့ရာတွင်၊ အချို့သောအချက်ကိုကျော်လွန်ပါက၊ ကွဲလွဲမှုသည် လျင်မြန်စွာလျော့နည်းသွားပြီး ကိန်းဂဏန်းများ ကျဆင်းခြင်းသည် ၎င်းတို့ကို သိသိသာသာလျှော့တွက်ခြင်းဆီသို့ ဦးတည်စေပြီး ဘက်လိုက်မှုတွင် သိသိသာသာတိုးလာစေသည်။

ဘက်လိုက်မှု နှင့် ကွဲပြားမှုကြား အကောင်းမွန်ဆုံးသော အပေးအယူကို ထုတ်ပေးသည့် λ တန်ဖိုးကို ရွေးချယ်သောအခါ စမ်းသပ်မှု၏ MSE သည် အနိမ့်ဆုံးဖြစ်ကြောင်း ဂရပ်မှ မြင်တွေ့နိုင်သည်။

λ = 0 ဖြစ်သောအခါ၊ တောင်ကြောဆုတ်ယုတ်ခြင်းရှိ ပြစ်ဒဏ်သက်တမ်းသည် အကျိုးသက်ရောက်မှုမရှိသဖြင့် တူညီသောကိန်းဂဏန်းခန့်မှန်းချက်ကို အနည်းဆုံးစတုရန်းအဖြစ်ထုတ်ပေးသည်။ သို့သော်၊ အချို့သောအချက်တစ်ခုသို့ λ ကိုတိုးမြှင့်ခြင်းဖြင့်၊ ကျွန်ုပ်တို့သည် စမ်းသပ်မှု၏ MSE တစ်ခုလုံးကို လျှော့ချနိုင်သည်။

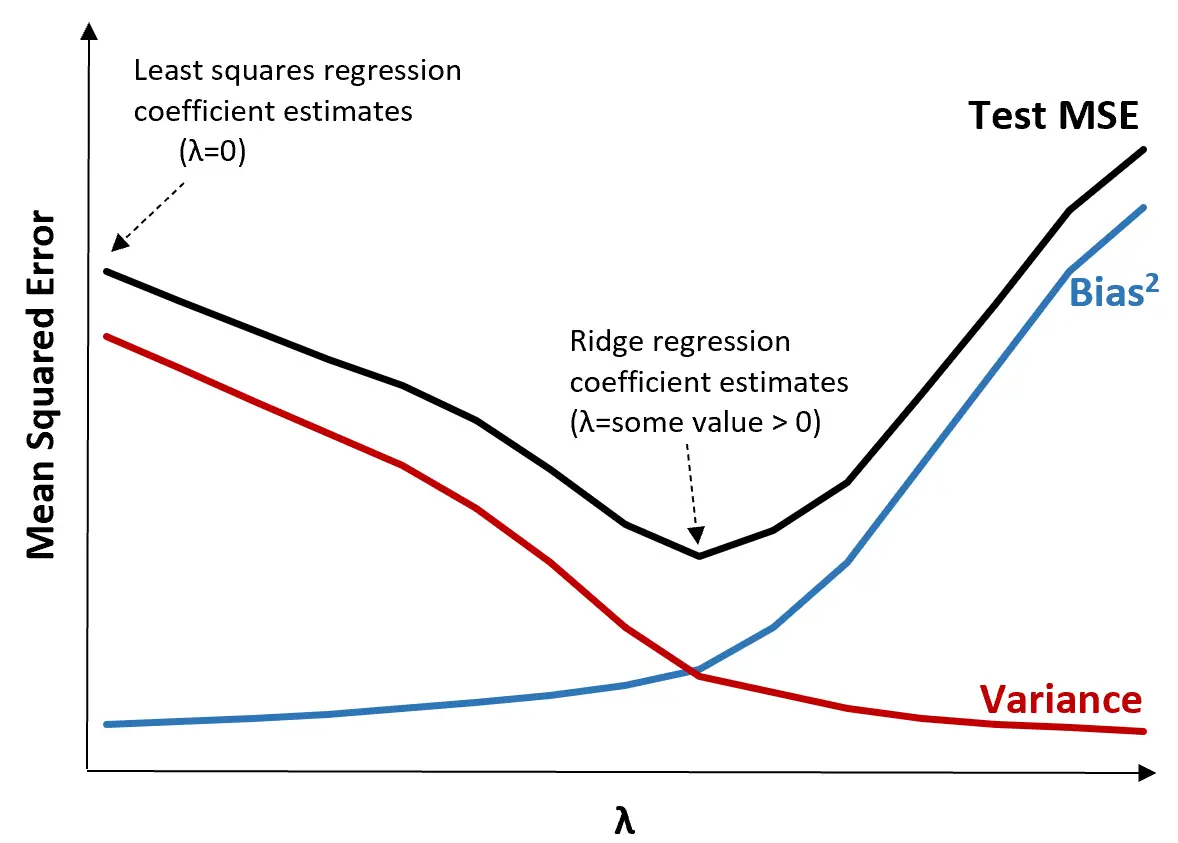
ဆိုလိုသည်မှာ အခေါင်ဆုတ်ယုတ်မှုဖြင့် အံဝင်ခွင်ကျဖြစ်သော မော်ဒယ်သည် လေးထောင့်အနိမ့်ဆုံး ဆုတ်ယုတ်မှုဖြင့် အံဝင်ခွင်ကျဖြစ်သော မော်ဒယ်ထက် သေးငယ်သော စမ်းသပ်မှုအမှားများကို ထုတ်ပေးမည်ကို ဆိုလိုသည်။

Ridge Regression ကို လက်တွေ့လုပ်ဆောင်ရန် အဆင့်များ

တောင်ကြောဆုတ်ယုတ်မှုကို လုပ်ဆောင်ရန် အောက်ပါအဆင့်များကို အသုံးပြုနိုင်ပါသည်။

အဆင့် 1- ခန့်မှန်းသူကိန်းရှင်များအတွက် ဆက်စပ်မက်ထရစ်နှင့် VIF တန်ဖိုးများကို တွက်ချက်ပါ။

ပထမဦးစွာ၊ ကျွန်ုပ်တို့သည် ဆက်စပ်မက်ထရစ် တစ်ခုကို ထုတ်လုပ်ရန်နှင့် ခန့်မှန်းသူကိန်းရှင်တစ်ခုစီအတွက် VIF (variance inflation factor) တန်ဖိုးများကို တွက်ချက်ရန် လိုအပ်သည်။

ကြိုတင်ခန့်မှန်းကိန်းရှင်များနှင့် မြင့်မားသော VIF တန်ဖိုးများအကြား ခိုင်မာသောဆက်စပ်မှုကို ကျွန်ုပ်တို့တွေ့ရှိပါက (အချို့သောစာများတွင် “ မြင့်မားသော” VIF တန်ဖိုးကို 5 အဖြစ်သတ်မှတ်ထားသော်လည်း အချို့က 10 ကိုအသုံးပြုသည်)၊ ထို့နောက် ခေါင်ဆုတ်ယုတ်မှုသည် သင့်လျော်ပါသည်။

သို့သော်၊ ဒေတာတွင် multicollinearity မရှိပါက၊ ၎င်းသည် ပထမနေရာ၌ ခေါင် regression လုပ်ဆောင်ရန် မလိုအပ်ပါ။ ယင်းအစား၊ ကျွန်ုပ်တို့သည် သာမန်အနည်းဆုံး လေးထောင့်ဆုတ်ယုတ်မှုကို လုပ်ဆောင်နိုင်သည်။

အဆင့် 2- ခန့်မှန်းသူကိန်းရှင်တစ်ခုစီကို စံသတ်မှတ်ပါ။

ridge regression ကိုမလုပ်ဆောင်မီ၊ ခန့်မှန်းသူကိန်းရှင်တစ်ခုစီတွင် 0 နှင့် 1 စံသွေဖည်ရှိသည်ဟူသော ဒေတာကို စကေးချရန် လိုအပ်ပါသည်။ ၎င်းသည် ခေါင်ဆုတ်ယုတ်မာမှုကို လုပ်ဆောင်သောအခါတွင် ခန့်မှန်းသူကိန်းရှင်တစ်ခုမှ လွန်ကဲလွှမ်းမိုးမှုရှိကြောင်း သေချာစေပါသည်။

အဆင့် 3- အခေါင်ဆုတ်ယုတ်မှုပုံစံကို ကိုက်ညီပြီး λ အတွက် တန်ဖိုးတစ်ခုကို ရွေးပါ။

λ အတွက် မည်သည့်တန်ဖိုးကို အသုံးပြုရမည်ကို ဆုံးဖြတ်ရန် ကျွန်ုပ်တို့ အသုံးပြုနိုင်သည့် တိကျသော ဖော်မြူလာမရှိပါ။ လက်တွေ့တွင် λ ကိုရွေးချယ်ရန် ဘုံနည်းလမ်းနှစ်ခုရှိသည်။

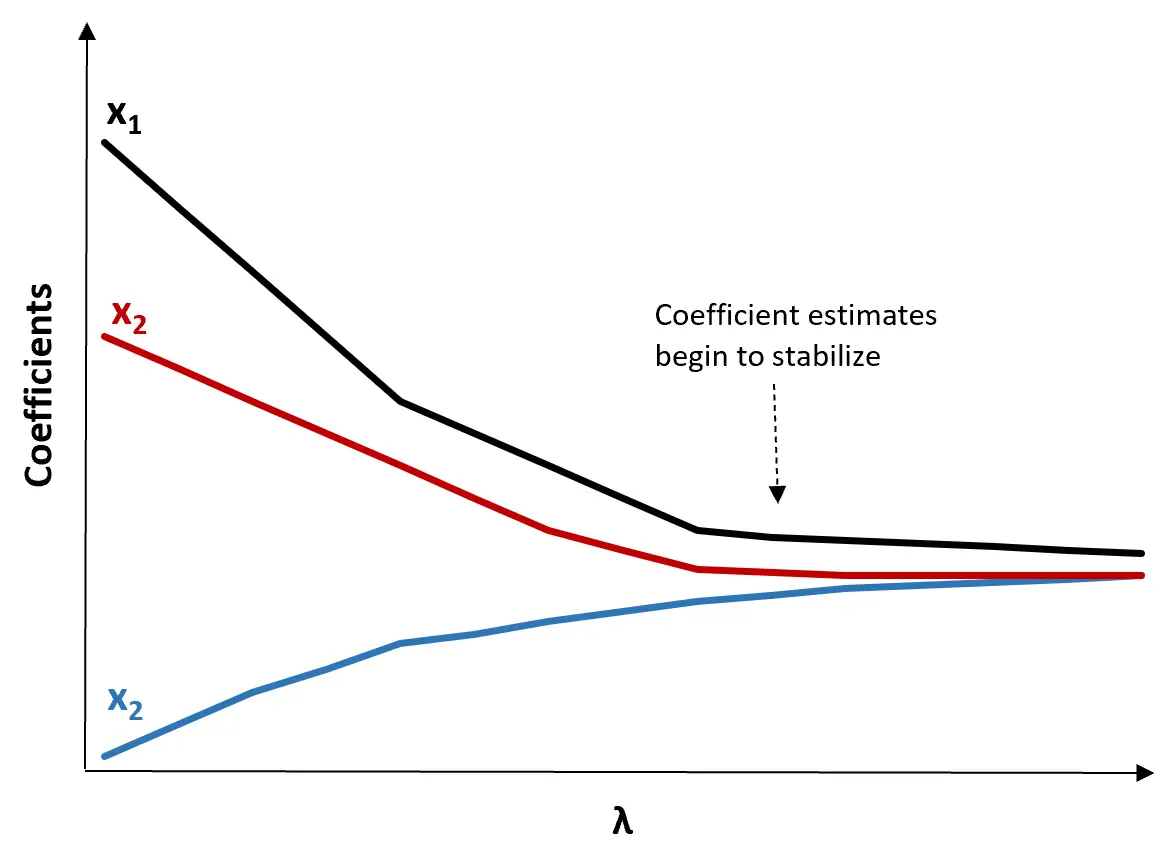
(၁) Ridge ခြေရာကောက်ကွက်တစ်ခုကို ဖန်တီးပါ။ ၎င်းသည် λ အနန္တသို့ တိုးလာသည်နှင့်အမျှ ကိန်းဂဏန်း ခန့်မှန်းချက်များ၏ တန်ဖိုးများကို မြင်ယောင်စေသည့် ဂရပ်တစ်ခုဖြစ်သည်။ ပုံမှန်အားဖြင့်၊ ကျွန်ုပ်တို့သည် ကိန်းဂဏန်းခန့်မှန်းချက်အများစုကို တည်ငြိမ်စပြုသည့်တန်ဖိုးအဖြစ် λ ကို ရွေးချယ်သည်။

(၂) λ တန်ဖိုးတစ်ခုစီအတွက် MSE စာမေးပွဲကို တွက်ချက်ပါ။

λ ကို ရွေးချယ်ရန် နောက်တစ်နည်းမှာ မော်ဒယ်တစ်ခုစီ၏ စမ်းသပ်မှု MSE ကို λ ၏ တန်ဖိုးများ ကွဲပြားစွာ တွက်ချက်ပြီး အနိမ့်ဆုံး စမ်းသပ် MSE တန်ဖိုးအဖြစ် λ ကို ရွေးချယ်ရန် ဖြစ်သည်။

Ridge Regression ၏ အားသာချက်များနှင့် အားနည်းချက်များ

Ridge regression ၏အကြီးမားဆုံး အားသာချက် မှာ multicollinearity ရှိနေချိန်တွင် အနည်းဆုံးစတုရန်းများထက်နိမ့်သော test mean square error (MSE) ကိုထုတ်လုပ်နိုင်ခြင်းဖြစ်သည်။

သို့သော်လည်း၊ Ridge ဆုတ်ယုတ်မှု၏ အကြီးမားဆုံး အားနည်းချက် မှာ နောက်ဆုံးပုံစံတွင် ကြိုတင်ခန့်မှန်းနိုင်သောကိန်းရှင်များ အားလုံးပါဝင်သောကြောင့် ပြောင်းလဲနိုင်သောရွေးချယ်မှုကို မလုပ်ဆောင်နိုင်ခြင်းဖြစ်သည်။ အချို့သော ခန့်မှန်းချက်များကို သုညနှင့် အလွန်နီးကပ်စွာ လျှော့ချမည်ဖြစ်သောကြောင့်၊ ၎င်းသည် မော်ဒယ်ရလဒ်များကို အနက်ဖွင့်ရန် ခက်ခဲစေသည်။

လက်တွေ့တွင်၊ Ridge regression သည် အနည်းဆုံး စတုရန်းမော်ဒယ်နှင့် နှိုင်းယှဉ်ပါက ပိုမိုကောင်းမွန်သော ခန့်မှန်းချက်များကို ထုတ်ပေးနိုင်သော မော်ဒယ်ကို ထုတ်လုပ်ရန် အလားအလာရှိသော်လည်း မော်ဒယ်၏ ရလဒ်များကို အဓိပ္ပာယ်ဖွင့်ဆိုရန် မကြာခဏ ခက်ခဲပါသည်။

မော်ဒယ်အဓိပ္ပာယ်ဖွင့်ဆိုခြင်း သို့မဟုတ် ခန့်မှန်းချက်တိကျမှုသည် သင့်အတွက် ပိုအရေးကြီးသည်ဆိုခြင်းအပေါ် မူတည်၍ မတူညီသောအခြေအနေများတွင် သာမန်အနိမ့်ဆုံးစတုရန်းများ သို့မဟုတ် အခေါင်ဆုတ်ယုတ်မှုကို သင်ရွေးချယ်နိုင်သည်။

R & Python တွင် Ridge Regression

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် R နှင့် Python တွင် ခေါင်ဆုတ်ဆုတ်ယုတ်ခြင်းကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားပြီး၊ ခေါင်ဆုတ်ယုတ်မာမှုပုံစံများနှင့် လိုက်လျောညီထွေဖြစ်စေရန်အတွက် အသုံးအများဆုံးဘာသာစကားနှစ်ခုဖြစ်သော R နှင့် Python

R in Ridge Regression (တစ်ဆင့်ပြီးတစ်ဆင့်)
Python ရှိ Ridge Regression (တစ်ဆင့်ပြီးတစ်ဆင့်)