တွဲထားသော နမူနာများ t-test- အဓိပ္ပါယ်၊ ဖော်မြူလာနှင့် ဥပမာ

နမူနာတစ်ခုရှိ ရှုမြင်မှု တစ်ခုစီရှိ အခြားနမူနာတစ်ခုရှိ စူးစမ်းမှုတစ်ခုနှင့် ဆက်စပ်နိုင်သောအခါ နမူနာနှစ်ခု၏နည်းလမ်းကို နှိုင်းယှဉ်ရန် တွဲထားသောနမူနာကို t-test ကို အသုံးပြုသည်။

ဤသင်ခန်းစာတွင် အောက်ပါတို့ကို ရှင်းပြထားသည်။

• တွဲထားသောနမူနာများကို t-test လုပ်ဆောင်ရန် စေ့ဆော်မှု။
• တွဲထားသောနမူနာများကို t-test လုပ်ဆောင်ရန်အတွက် ဖော်မြူလာ။
• တွဲထားသောနမူနာများကို t-test ပြုလုပ်ရန် ကိုက်ညီရမည့် ယူဆချက်များ။
• တွဲထားသောနမူနာများကို t-test လုပ်နည်း ဥပမာ။

တွဲထားသော နမူနာများ t-test- လှုံ့ဆော်မှု

တွဲထားသောနမူနာ t-test ကို အခြေအနေနှစ်ခုတွင် အများအားဖြင့် အသုံးပြုသည်-

1. ကုသမှုမခံယူမီနှင့် အပြီးတွင် ဘာသာရပ်တစ်ခုကို တိုင်းတာခြင်းဖြစ်သည် – ဥပမာ၊ ကောလိပ်ဘတ်စကတ်ဘောကစားသမားများ၏ အများဆုံး ဒေါင်လိုက်ခုန်ခြင်းကို လေ့ကျင့်ရေးအစီအစဉ်တွင် မပါဝင်မီနှင့် အပြီးတွင် တိုင်းတာသည်။

2. တိုင်းတာမှုတစ်ခုအား မတူညီသောအခြေအနေနှစ်ခုအောက်တွင်ပြုလုပ်သည် – ဥပမာ၊ လူနာတစ်ဦး၏တုံ့ပြန်မှုအချိန်ကို မတူညီသောဆေးဝါးနှစ်ခုဖြင့်တိုင်းတာသည်။

ဖြစ်ရပ်နှစ်ခုစလုံးတွင်၊ နမူနာတစ်ခုမှ ရှုမြင်မှုတစ်ခုစီမှ အခြားနမူနာတစ်ခုမှ စူးစမ်းလေ့လာမှုတစ်ခုနှင့် ဆက်စပ်နိုင်သည့် အုပ်စုနှစ်ခုကြားရှိ ပျမ်းမျှတိုင်းတာမှုကို ကျွန်ုပ်တို့ နှိုင်းယှဉ်လိုပါသည်။

တွဲထားသော နမူနာများ t-test- ဖော်မြူလာ

တွဲထားသောနမူနာ t-test သည် အောက်ပါ null hypothesis ကို အမြဲသုံးသည်-

• H ₀ : μ ₁ = μ ₂ (လူဦးရေ နှစ်ခုသည် တူညီသည်)

အခြားယူဆချက်သည် နှစ်ဘက်၊ ဘယ် သို့မဟုတ် ညာဘက် ဖြစ်နိုင်သည်-

• H ₁ (အမြီးနှစ်ကောင်): μ ₁ ≠ μ ₂ (လူဦးရေနှစ်ခု၏ အဓိပ္ပါယ်မှာ မညီမျှခြင်း)
• H ₁ (ဘယ်ဘက်): μ ₁ < μ ₂ (လူဦးရေ 1 ၏ပျမ်းမျှသည် လူဦးရေ 2 ၏ပျမ်းမျှထက်နိမ့်သည်)
• H ₁ (ညာဘက်): μ ₁ > μ ₂ (လူဦးရေ 1 ၏ပျမ်းမျှသည် လူဦးရေ 2 ၏ပျမ်းမျှထက် ပိုများသည်)

ကျွန်ုပ်တို့သည် t-test ကိန်းဂဏန်းကိုတွက်ချက်ရန် အောက်ပါဖော်မြူလာကို အသုံးပြုပါသည်။

t = x _diff / (s _diff /√n)

ရွှေ-

• x _diff : ပျမ်းမျှကွဲပြားမှုများ၏ ဥပမာ
• s- စံသွေဖည်ကွဲပြားမှုများ၏ ဥပမာ
• n- နမူနာအရွယ်အစား (ဆိုလိုသည်မှာ အတွဲအရေအတွက်)

လွတ်လပ်မှု (n-1) ဒီဂရီနှင့် t-test ကိန်းဂဏန်းနှင့် သက်ဆိုင်သော p-တန်ဖိုးသည် ရွေးချယ်ထားသော အရေးပါမှုအဆင့်ထက် နည်းနေပါက (အများအားဖြင့် ရွေးချယ်မှုများမှာ 0.10၊ 0.05၊ နှင့် 0.01)၊ ထို့နောက် null hypothesis ကို ငြင်းပယ်နိုင်ပါသည်။

တွဲထားသော နမူနာများ t-test- ယူဆချက်

တွဲထားသောနမူနာ t-test ၏ရလဒ်များ တရားဝင်စေရန်အတွက်၊ အောက်ပါ ယူဆချက်များနှင့် ကိုက်ညီရမည်-

• ပါဝင်သူများသည် လူဦးရေထဲမှ ကျပန်းရွေးချယ်သင့်သည်။
• အတွဲများကြား ခြားနားချက်များကို ခန့်မှန်းခြေအားဖြင့် ပုံမှန်ဖြန့်ဝေသင့်သည်။
• ကွဲပြားမှုများတွင် လွန်ကဲသော ကွဲပြားမှုများ မရှိသင့်ပါ။

တွဲထားသော နမူနာ t-test : ဥပမာ

ကောလိပ်ဘတ်စကက်ဘောကစားသမားများ၏ အမြင့်ဆုံးဒေါင်လိုက်ခုန်ခြင်း (လက်မအတွင်း) လေ့ကျင့်ရေးအစီအစဉ်တစ်ခုသည် ကျွန်ုပ်တို့ သိချင်သည်ဆိုပါစို့။

၎င်းကိုစမ်းသပ်ရန်အတွက်၊ ကျွန်ုပ်တို့သည် ကောလိပ်ဘတ်စကတ်ဘောကစားသမား 20 ဦး၏ ရိုးရှင်းသောကျပန်းနမူနာ တစ်ခုကို စုဆောင်းကာ ၎င်းတို့၏ အများဆုံးဒေါင်လိုက်ခုန်ခြင်းတစ်ခုစီကို တိုင်းတာနိုင်ပါသည်။ ထို့နောက် ကစားသမားတစ်ဦးစီအား တစ်လကြာ လေ့ကျင့်ရေးအစီအစဉ်ကို အသုံးပြုကာ လကုန်တွင် ၎င်းတို့၏အမြင့်ဆုံးဒေါင်လိုက်ခုန်ခြင်းကို ထပ်မံတိုင်းတာနိုင်သည်။

လေ့ကျင့်ရေးပရိုဂရမ်သည် အမြင့်ဆုံးဒေါင်လိုက်ခုန်ခြင်းအပေါ် အမှန်တကယ်အကျိုးသက်ရောက်မှုရှိမရှိ ဆုံးဖြတ်ရန်၊ အောက်ပါအဆင့်များကို အသုံးပြု၍ α = 0.05 အရေးပါမှုအဆင့်တွင် တွဲဖက်နမူနာများ t-test ကို လုပ်ဆောင်ပါမည်။

အဆင့် 1- ကွဲပြားမှုများအတွက် အကျဉ်းချုပ်ဒေတာကို တွက်ချက်ပါ။

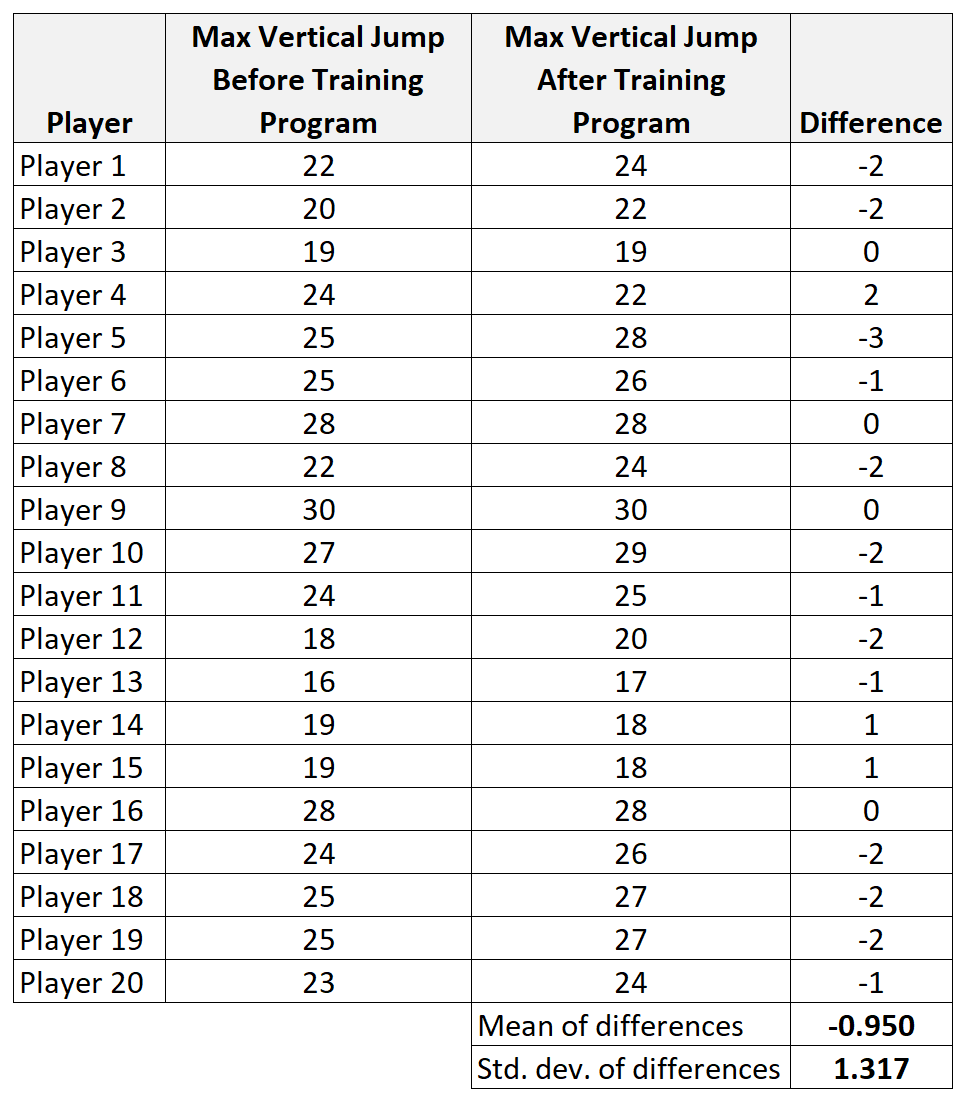
• x _diff : နမူနာ ပျမ်းမျှ ကွာခြားချက်များ = -0.95
• s: နမူနာစံသွေဖည်ကွဲပြားမှု = 1.317
• n: နမူနာအရွယ်အစား (အတွဲအရေအတွက်) = 20

အဆင့် 2- ယူဆချက်များကို သတ်မှတ်ပါ။

အောက်ဖော်ပြပါ ယူဆချက်များနှင့် တွဲဖက်နမူနာများအတွက် t-test ကို လုပ်ဆောင်ပါမည်။

• H ₀ : μ ₁ = μ ₂ (လူဦးရေ နှစ်ခုသည် တူညီသည်)
• H ₁ : μ ₁ ≠ μ ₂ (လူဦးရေ နှစ်ခု အဓိပ္ပါယ်မှာ မညီမျှခြင်း)

အဆင့် 3- t -test ကိန်းဂဏန်းကိုတွက်ချက်ပါ။

t = x _diff / (s _diff /√n) = -0.95 / (1.317/ √ 20) = -3.226၊

အဆင့် 4- t- စမ်းသပ်စာရင်းအင်း၏ p-တန်ဖိုးကို တွက်ချက်ပါ။

P Value calculator သို့ T ရမှတ် အရ t = -3.226 နှင့် ဆက်စပ်သော p တန်ဖိုး နှင့် လွတ်လပ်မှုဒီဂရီ = n-1 = 20-1 = 19 သည် 0.00445 ဖြစ်သည်။

အဆင့် 5- ကောက်ချက်ဆွဲပါ။

ဤ p-value သည် ကျွန်ုပ်တို့၏ အရေးပါမှုအဆင့် α = 0.05 အောက်ဖြစ်သောကြောင့်၊ ကျွန်ုပ်တို့သည် null hypothesis ကို ငြင်းပယ်ပါသည်။ ကစားသမားများ၏ ပျမ်းမျှအမြင့်ဆုံး ဒေါင်လိုက်ခုန်ခြင်းသည် လေ့ကျင့်ရေးအစီအစဉ်တွင် မပါဝင်မီနှင့် အပြီးတွင် ကွဲပြားသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထားရှိသည်။

မှတ်ချက်- တွဲထားသောနမူနာ t- test ဂဏန်းတွက်စက်ကို အသုံးပြု၍ ဤတွဲစပ်နမူနာ t- test တစ်ခုလုံးကိုလည်း လုပ်ဆောင်နိုင်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် မတူညီသော စာရင်းအင်းပရိုဂရမ်များကို အသုံးပြု၍ တွဲထားသော နမူနာ t-test ကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

Excel တွင်တွဲထားသောနမူနာများကို t-test လုပ်နည်း
SPSS တွင် တွဲထားသော နမူနာ t-test ကို မည်သို့လုပ်ဆောင်ရမည်နည်း။
Stata တွင်တွဲထားသောနမူနာများကို t-test လုပ်နည်း
TI-84 ဂဏန်းတွက်စက်ပေါ်တွင် Paired-Sample t-Test ကို မည်သို့လုပ်ဆောင်ရမည်နည်း။
R တွင်တွဲထားသောနမူနာများကို t-test လုပ်နည်း
Python တွင် တွဲထားသော နမူနာ t-test ကို မည်သို့လုပ်ဆောင်ရမည်နည်း။
Paired Samples T-Test ကို လက်ဖြင့်ပြုလုပ်နည်း