အတိုးနှုန်း ဖြန့်ဖြူးခြင်း။
ဤဆောင်းပါးတွင် ကိန်းဂဏန်းစာရင်းဇယားတွင် အတိုးကိန်းဖြန့်ဖြူးမှုမှာ အဘယ်အရာနှင့် ၎င်းကိုအသုံးပြုကြောင်း ရှင်းပြထားသည်။ အလားတူပင်၊ exponential ဖြန့်ဖြူးမှု၏ ဂုဏ်သတ္တိများအပြင် ၎င်း၏ဖော်မြူလာများ၊ ၎င်း၏ဂရပ်များနှင့် ဖြေရှင်းထားသော လေ့ကျင့်ခန်းကို သင်တွေ့လိမ့်မည်။ ထို့အပြင်၊ သင်သည် အွန်လိုင်း ကိန်းဂဏန်းဖြန့်ချီရေး ဂဏန်းတွက်စက်ဖြင့် ဖြစ်နိုင်ခြေမှန်သမျှကို တွက်ချက်နိုင်မည်ဖြစ်သည်။
ကိန်းဂဏန်းဖြန့်ချီခြင်းဆိုသည်မှာ အဘယ်နည်း။
ကိန်းဂဏန်းဖြန့်ချီမှုသည် ကျပန်းဖြစ်စဉ်တစ်ခုဖြစ်ပေါ်လာခြင်းအတွက် စောင့်ဆိုင်းချိန်ကို နမူနာယူရန် အသုံးပြုသည့် စဉ်ဆက်မပြတ်ဖြစ်နိုင်ခြေဖြန့်ဖြူးမှုတစ်ခုဖြစ်သည်။
ပိုတိကျသည်မှာ၊ ကိန်းဂဏန်းဖြန့်ချီမှုသည် Poisson ဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်ရပ်နှစ်ခုကြား စောင့်ဆိုင်းချိန်ကို ဖော်ပြနိုင်စေပါသည်။ ထို့ကြောင့် ကိန်းဂဏန်းဖြန့်ချီမှုသည် Poisson ဖြန့်ဖြူးမှုနှင့် နီးကပ်စွာဆက်စပ်နေသည်။
ကိန်းဂဏန်းဖြန့်ချီမှုတွင် ဂရိအက္ခရာ λ ဖြင့် ကိုယ်စားပြုသည့် ဝိသေသ ဘောင်တစ်ခုရှိပြီး သတ်မှတ်ကာလတစ်ခုအတွင်း လေ့လာထားသည့် ဖြစ်ရပ်ကို မျှော်မှန်းထားသည့် အကြိမ်အရေအတွက်ကို ညွှန်ပြသည်။
![]()
အလားတူ၊ မအောင်မြင်မချင်း အချိန်ကာလကို ပုံသေသတ်မှတ်ရန်အတွက်လည်း ထပ်ကိန်းခွဲဝေမှုကိုလည်း အသုံးပြုပါသည်။ ထို့ကြောင့် exponential ဖြန့်ဖြူးမှုတွင် ယုံကြည်စိတ်ချရမှုနှင့် ရှင်သန်မှုသီအိုရီတွင် အသုံးချမှုများစွာရှိသည်။
Exponential Distributions နမူနာများ
ယခု ကျွန်ုပ်တို့သည် ထပ်ကိန်းဖြန့်ချီခြင်း၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို သိရှိပြီး သဘောတရားကို ပိုမိုနားလည်ရန် ဤဖြန့်ဖြူးမှုအမျိုးအစား၏ ဥပမာများစွာကို ကြည့်ကြပါစို့။
ထပ်ကိန်းခွဲဝေခြင်း၏ ဥပမာများ-
- ခေါ်ဆိုမှုစင်တာတစ်ခုရှိ ခေါ်ဆိုမှုနှစ်ခုကြား ကုန်ဆုံးသွားသည့်အချိန်။
- လူတစ်ဦးသည် သီးခြားလမ်းတစ်ခုပေါ်တွင် အလကား တက္ကစီတစ်စီး ဖြတ်သွားသည်အထိ စောင့်ရမည့်အချိန်။
- ဖောက်သည်အသစ်တစ်ဦးစတိုးဆိုင်ထဲသို့ဝင်သည်အထိစောင့်ဆိုင်းအချိန်။
- ဝဘ်စာမျက်နှာသို့ ဝင်ရောက်သည့် မတူညီသော အသုံးပြုသူ နှစ်ဦးကြား ကုန်သွားသော အချိန်။
- လေယာဉ်တစ်စင်းမှ ထွက်ခွာချိန်နှင့် အခြားလေယာဉ်တစ်စင်းမှ ထွက်ခွာချိန်ကြားရှိ လေဆိပ်တစ်ခုတွင် အချိန်ကုန်သွားသည်။
အညွှန်းကိန်း ဖြန့်ဝေမှု ဖော်မြူလာ
ကိန်းဂဏန်းဖြန့်ချီမှုဖြစ်နိုင်ခြေကို တွက်ချက်သတ်မှတ်သည့် သိပ်သည်းဆလုပ်ဆောင်ချက်ဖော်မြူလာသည် λ နှင့် ညီမျှသော နံပါတ် e ဖြင့် မြှောက်ထားသော အနှုတ် λ အမြှောက် x ၏ပါဝါ။
တစ်နည်းအားဖြင့်၊ ထပ်ကိန်းဖြန့်ချီမှုဖြစ်နိုင်ခြေကို တွက်ချက်ရန်အတွက် ဖော်မြူလာ မှာ အောက်ပါအတိုင်းဖြစ်သည်-

👉 exponential ဖြန့်ဖြူးမှုနောက်ဆက်တွဲဖြစ်သော variable ၏ဖြစ်နိုင်ခြေကိုတွက်ချက်ရန် အောက်ပါ calculator ကိုသင်အသုံးပြုနိုင်ပါသည်။
အခြားတစ်ဖက်တွင်၊ ထပ်ကိန်းထုတ်ခြင်း၏ တိုးပွားနိုင်ခြေကို တွက်ချက်ရန် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်။
![]()
အညွှန်းကိန်း ဖြန့်ဖြူးမှု ဂရပ်
ဤအပိုင်းတွင် သိပ်သည်းဆလုပ်ဆောင်မှုနှင့် ဖြန့်ချီမှုဆိုင်ရာ ဂရပ်ဖစ်ဆိုင်ရာ ကိုယ်စားပြုမှုကို သင်မြင်နိုင်သည်။
အောက်ဖော်ပြပါ တွင် ပါရာမီတာ λ ၏ တန်ဖိုးအပေါ် မူတည်၍ ထပ်ကိန်းဖြန့်ချီမှု၏ သိပ်သည်းဆလုပ်ဆောင်မှု၏ ဂရပ်သည် မည်ကဲ့သို့ ကွဲပြားသည်ကို အောက်တွင် ကြည့်ရှုနိုင်ပါသည်။
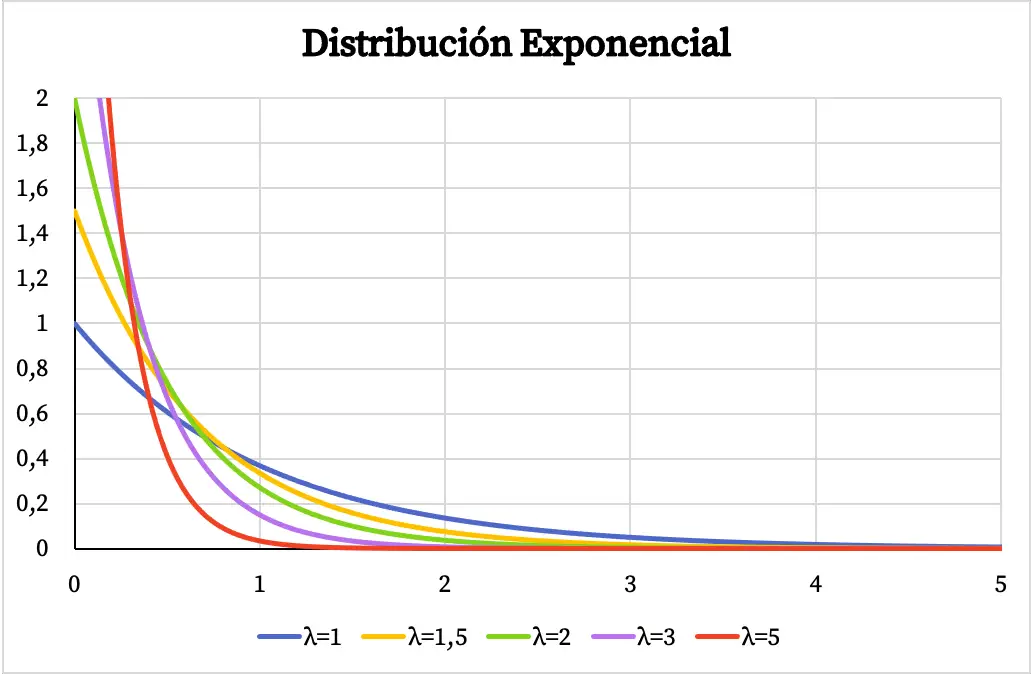
အလားတူပင်၊ ထပ်ကိန်းဖြန့်ချီမှု၏ တိုးပွားလာနိုင်သည့် ဖြစ်နိုင်ခြေလုပ်ဆောင်ချက်သည် အောက်ပါဂရပ်တွင် သင်တွေ့မြင်နိုင်သကဲ့သို့ ပါရာမီတာ λ ၏တန်ဖိုးပေါ်တွင်လည်း မူတည်ပါသည်။
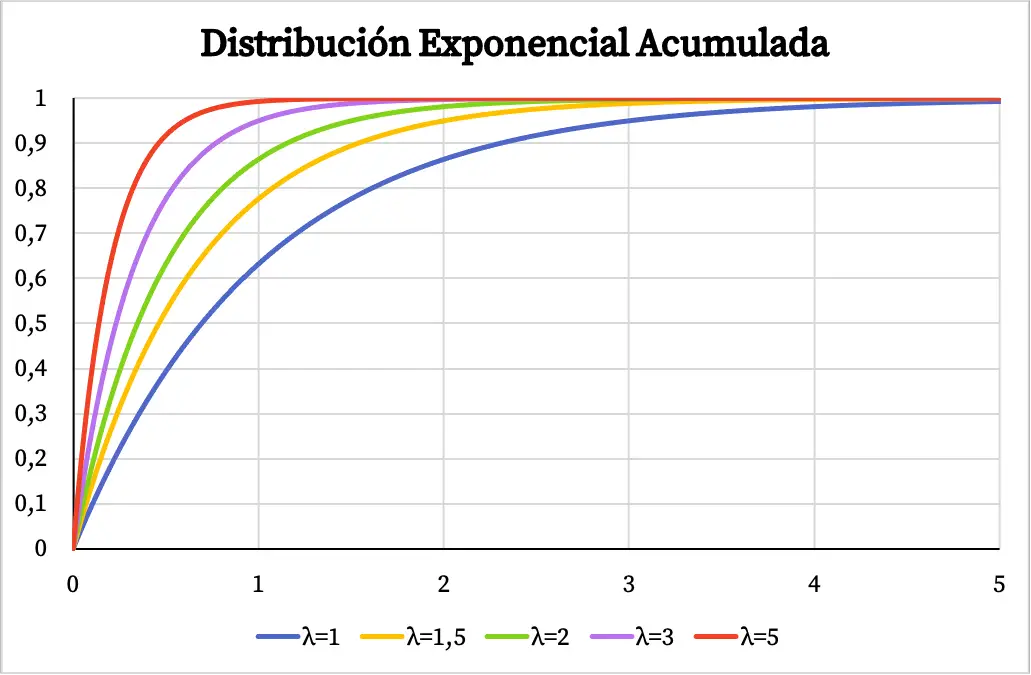
ကိန်းဂဏန်းဖြန့်ချီမှုဆိုင်ရာ လေ့ကျင့်ခန်းကို ဖြေရှင်းခဲ့သည်။
- ပျမ်းမျှအားဖြင့်၊ λ=1 အသုံးပြုသူများ/မိနစ်သည် သီးခြားဝဘ်စာမျက်နှာတစ်ခုကို ဝင်ရောက်ကြည့်ရှုသည်။ အသုံးပြုသူနှစ်ဦးကြား ဝင်ရောက်သည့်အချိန်သည် 3 မိနစ်ဖြစ်နိုင်ခြေ မည်မျှရှိသနည်း။ နှင့် 2 မိနစ်ထက်နည်းသော သို့မဟုတ် ညီမျှခြင်းဖြစ်နိုင်ခြေ။
ဤပြဿနာ၏ ကျပန်းပြောင်းလွဲမှုကို သတ်မှတ်သည့် ဖြန့်ဖြူးမှုသည် အဖြစ်အပျက်တစ်ခု (ဝဘ်စာမျက်နှာပေါ်ရှိ အသုံးပြုသူတစ်ဦး၏ ဝင်ရောက်မှု) မှ ဤတူညီသောဖြစ်ရပ်တစ်ခု ထပ်မံမဖြစ်ပွားမီအထိ ကျွန်ုပ်တို့သည် ကိန်းဂဏန်းဖြန့်ဝေမှုတစ်ခုဖြစ်သည်။
![]()
ထို့ကြောင့်၊ မတူညီသောအသုံးပြုသူနှစ်ဦး၏ဝင်ရောက်မှုကြားတွင်ကုန်ဆုံးသွားသောဖြစ်နိုင်ခြေကိုတွက်ချက်ရန်၊ ကျွန်ုပ်တို့သည် သိပ်သည်းဆလုပ်ဆောင်ချက်ဖော်မြူလာကိုအသုံးပြုရန်လိုအပ်သည် (အထက်တွင်ကြည့်ပါ)။
![Rendered by QuickLaTeX.com \begin{aligned}P[X=x]&=\lambda e^{-\lambda x}\\[2ex]P[X=3]&=1\cdot e^{-1\cdot 3}\\[2ex]P[X=3]&=0,05\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-4eb2d6e5190f313d74831763613683ec_l3.png)
အခြားတစ်ဖက်တွင်၊ စုစည်းမှုဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ရန်၊ ကျွန်ုပ်တို့သည် ထပ်ကိန်းဖြန့်ချီမှု၏ ဖြန့်ဝေမှုလုပ်ဆောင်ချက်ဖော်မြူလာကို အသုံးပြုရပါမည်-
![Rendered by QuickLaTeX.com \begin{aligned}P[X\leq x]&=1- e^{-\lambda x}\\[2ex]P[X\leq 2]&=1-e^{-1\cdot 2}\\[2ex]P[X\leq 2]&=0,86\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5ff6ef636fd31aec708b387669a68b93_l3.png)
ထပ်ကိန်းဖြန့်ချီခြင်း၏ လက္ခဏာများ
ကိန်းဂဏန်းဖြန့်ချီမှုတွင် အောက်ပါလက္ခဏာများ ရှိသည်။
- exponential ဖြန့်ဖြူးမှုတွင် ထူးခြားသော ကန့်သတ်ဘောင်တစ်ခု λ ပါရှိပြီး၊ ၎င်းမှာ လေ့လာထားသည့် ဖြစ်စဉ်ကို ပေးထားသည့် အချိန်ကာလအတွင်း ဖြစ်ပေါ်လာမည့် အကြိမ်အရေအတွက်ကို ညွှန်ပြသည်။
![]()
- ကိန်းဂဏန်းဖြန့်ချီမှုတွင် အနုတ်တန်ဖိုးကို မယူနိုင်ပါ၊ ထို့ကြောင့် ကိန်းဂဏန်းဖြန့်ချီမှု၏ ဒိုမိန်းတွင် သုညထက်ကြီးသော သို့မဟုတ် သုညထက်ကြီးသော အစစ်အမှန်ကိန်းဂဏန်းများအားလုံး ပါဝင်ပါသည်။
![]()
- exponential distribution ၏ ပျမ်းမျှသည် characteristic parameter λ ဖြင့် ပိုင်းထားသော တစ်ခုနှင့် ညီမျှသည်။
![]()
- ကိန်းဂဏန်းဖြန့်ချီမှု၏ကွဲလွဲမှုသည် ၎င်း၏ပျမ်းမျှနှစ်ထပ်ဖြစ်သောကြောင့်၊ ကိန်းဂဏန်းဖြန့်ချီမှု၏ကွဲလွဲမှုသည် coefficient λ နှစ်ထပ်ကိန်းကျော်တစ်ခုနှင့် ညီမျှသည်။
![]()
- λ ၏တန်ဖိုး မည်သို့ပင်ရှိစေကာမူ၊ ကိန်းဂဏန်းဖြန့်ချီမှု၏ အချိုးမညီသောကိန်းသည် 2 နှင့် အမြဲညီမျှသည်။
![]()
- အလားတူ၊ ကိန်းဂဏန်းဖြန့်ချီမှုတိုင်း၏ kurtosis coefficient သည် 9 နှင့် အမြဲတမ်းညီမျှသည်။
![]()
- exponential ဖြန့်ဖြူးမှု၏ သိပ်သည်းဆလုပ်ဆောင်ချက်အတွက် ဖော်မြူလာမှာ-
![]()
- ကိန်းဂဏန်းများ ဖြန့်ဝေမှု၏ တိုးပွားနိုင်ခြေဖြစ်နိုင်ခြေအတွက် ဖော်မြူလာမှာ အောက်ပါအတိုင်း ဖြစ်နေသော်လည်း၊
![]()
- ကိန်းဂဏန်းဖြန့်ချီမှုသည် မမ်မိုရီပြင်ပပိုင်ဆိုင်မှုနှင့်အတူ ဖြစ်နိုင်ချေနည်းသော ဖြန့်ဝေမှုများထဲမှ တစ်ခုဖြစ်သည်။ ဤပိုင်ဆိုင်မှု ဆိုသည်မှာ ယခင်ဖြစ်ရပ်တစ်ခု ပေါ်ပေါက်ခြင်းသည် အနာဂတ်တွင် ဖြစ်ပွားနိုင်ခြေရှိသော အဖြစ်အပျက်ကို သက်ရောက်မှု မရှိပါ။ ဥပမာအားဖြင့်၊ ကိန်းဂဏန်းဖြန့်ချီမှုတစ်ခုတွင်၊ အသုံးပြုသူအသစ်သည် တစ်မိနစ်ထက်နည်းသော ဝဘ်စာမျက်နှာကို ဝင်ရောက်ကြည့်ရှုမည့် ဖြစ်နိုင်ခြေမှာ အသုံးပြုသူသည် ယခုမှဝင်ရောက်ခြင်းရှိမရှိ သို့မဟုတ် အသုံးပြုသူမှ ဝင်ရောက်ခြင်းရှိမရှိပေါ်တွင်မူတည်မည်မဟုတ်ပါ။ ဆယ်မိနစ်ကျော်။
![P[X>x+y|X>y]=P[X>x]” title=” Rendered by QuickLaTeX.com” height=” 19″ width=” 254″ style=” vertical-align: -5px;” ></p>
</p>
<h2 class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-6f7c755e5b48eb203c51c97d7bc7ec7d_l3.png) Exponential Distribution Calculator
Exponential Distribution Calculator
ဖြစ်နိုင်ခြေကို တွက်ချက်ရန် အောက်ပါ ဂဏန်းပေါင်းစက်ထဲသို့ ပါရာမီတာ λ တန်ဖိုးနှင့် x တန်ဖိုးကို ထည့်ပါ။ သင်သည် တွက်ချက်လိုသော ဖြစ်နိုင်ခြေကို ရွေးချယ်ပြီး ဒဿမ ပိုင်းခြားခြင်းအဖြစ် အစက်ကို အသုံးပြု၍ ဂဏန်းများကို ထည့်ရန်၊ ဥပမာ 0.50။