ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှု

အားဖြင့် Benjamin Anderson ဩဂုတ် 2, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးသည် စာရင်းဇယားများတွင် ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှုအကြောင်း ရှင်းပြထားသည်။ အလားတူပင်၊ ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှုဖော်မြူလာ၊ ထောက်ပံ့ပို့ဆောင်ရေးဆုတ်ယုတ်မှု၏ ကွဲပြားသောအမျိုးအစားများနှင့်၊ ထို့အပြင် ဖြေရှင်းနိုင်သော ထောက်ပံ့ပို့ဆောင်ရေးဆုတ်ယုတ်မှုလေ့ကျင့်ခန်းကို သင်တွေ့လိမ့်မည်။

Logistic regression ဆိုတာ ဘာလဲ။

ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ ထောက်ပံ့ပို့ဆောင်ရေးဆုတ်ယုတ်မှု သည် အမျိုးအစား ကွဲပြားသောကိန်းရှင် ၏ရလဒ်ကို ခန့်မှန်းရန်အသုံးပြုသည့် ဆုတ်ယုတ်မှုပုံစံတစ်မျိုးဖြစ်သည်။ ဆိုလိုသည်မှာ၊ အမှီအခိုကင်းသော ကိန်းရှင်များပေါ်မူတည်၍ အချို့သောတန်ဖိုးတစ်ခုအပေါ် အမျိုးအစားအလိုက် ကိန်းရှင်၏ဖြစ်နိုင်ခြေကို နမူနာယူရန် ထောက်လှမ်းဆုတ်ယုတ်မှုကို အသုံးပြုသည်။

အသုံးအများဆုံး logistic regression model သည် binary logistic regression ဖြစ်ပြီး ဖြစ်နိုင်ချေ ရလဒ် နှစ်ခုသာရှိသည်- “ failure” သို့မဟုတ် “ success” ( Bernoulli distribution )။ “အောင်မြင်မှု” ကို တန်ဖိုး 0 ဖြင့် ကိုယ်စားပြုပြီး “အောင်မြင်မှု” ကို တန်ဖိုး 1 ဖြင့် ကိုယ်စားပြုသည်။

ဥပမာအားဖြင့်၊ ကျောင်းသားတစ်ဦးသည် ၎င်းတို့လေ့လာခဲ့သည့် နာရီများကိုအခြေခံ၍ စာမေးပွဲတစ်ခုအောင်မြင်နိုင်ခြေကို logistic regression model ကိုအသုံးပြု၍ လေ့လာနိုင်သည်။ ဤကိစ္စတွင်၊ ကျရှုံးမှုသည် “ ကျရှုံးခြင်း” ၏ရလဒ်ဖြစ်ပြီး အခြားတစ်ဖက်တွင်၊ အောင်မြင်မှုသည် “ အောင်မြင်မှု” ၏ရလဒ်ဖြစ်သည်။

Logistic Regression Formula

logistic regression model အတွက် ညီမျှခြင်းမှာ-

$\displaystyle \ln \left(\frac{p}{1-p}\right) =\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i$

ထို့ကြောင့်၊ ထောက်ပံ့ပို့ဆောင်ရေးဆိုင်ရာ ဆုတ်ယုတ်မှုပုံစံတစ်ခုတွင်၊ “ အောင်မြင်မှု” ရလဒ်ရရှိရန်ဖြစ်နိုင်ခြေ၊ ဆိုလိုသည်မှာ မှီခိုကိန်းရှင်သည် တန်ဖိုး 1 ကိုယူသည်ဟူသော ဖြစ်နိုင်ခြေကို အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်သည်-

$p=\cfrac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i)}}$

ရွှေ-

$p$

dependent variable သည် 1 ဖြစ်နိုင်ခြေဖြစ်သည်။
$\beta_0$

logistic regression model ၏ ကိန်းသေဖြစ်ပါသည်။
$\beta_i$

ကိန်းရှင် i ၏ ဆုတ်ယုတ်မှုကိန်း။
$x_i$

variable i ၏တန်ဖိုးဖြစ်သည်။

Logistic Regression Model ဥပမာ

ယခုကျွန်ုပ်တို့သည် logistic regression ၏အဓိပ္ပါယ်ကိုသိပြီး၊ ဤ regression အမျိုးအစား၏ပုံစံတစ်ခုကိုဖန်တီးပုံ၏ခိုင်မာသောဥပမာတစ်ခုကိုကြည့်ကြပါစို့။

အောက်ပါဇယားတွင်၊ ကျောင်းသားတစ်ဦးစီ၏ စာသင်ချိန်နှင့် စာရင်းအင်းစာမေးပွဲ အောင်မြင်သည်ဖြစ်စေ ကျရှုံးသည်ဖြစ်စေ ဆက်စပ်သော ဒေတာအပိုင်းအစ 20 ကို စုစည်းထားပါသည်။ ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှုပုံစံကို လုပ်ဆောင်ပြီး 4 နာရီကြာ လေ့လာပါက ကျောင်းသားတစ်ဦး အောင်မြင်နိုင်ခြေကို တွက်ချက်ပါ။

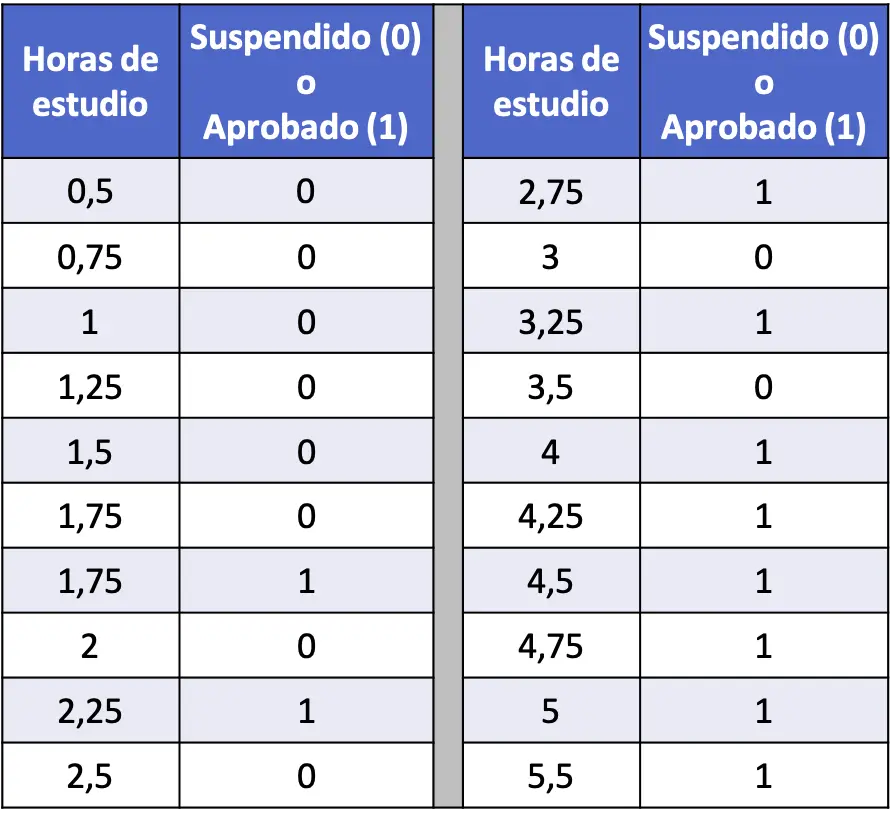
ဤအခြေအနေတွင်၊ ရှင်းလင်းချက်ပြောင်းနိုင်သောကိန်းရှင်သည် စာသင်ချိန်နာရီအရေအတွက်ဖြစ်ပြီး၊ ကျောင်းသားသည် ကျရှုံးသည်ဖြစ်စေ (0) သို့မဟုတ် (1) အောင်မြင်သည်ဖြစ်စေ တုံ့ပြန်မှုကိန်းရှင်ဖြစ်သည်။ ထို့ကြောင့် ကျွန်ုပ်တို့၏ မော်ဒယ်တွင် ကိန်းဂဏန်းများသာ ရှိပါမည်။

$\beta_0$

နှင့် ကိန်းဂဏန်း

$\beta_1$

လွတ်လပ်သော ကိန်းရှင်တစ်ခုသာရှိသောကြောင့်၊

$\beta_0 \qquad \beta_1$

regression coefficients ကို ကိုယ်တိုင်ဆုံးဖြတ်ခြင်းသည် အလွန်ပင်ပန်းသောကြောင့် Minitab ကဲ့သို့သော ကွန်ပျူတာဆော့ဖ်ဝဲကို အသုံးပြုရန် အကြံပြုထားသည်။ ထို့ကြောင့် Minitab ကိုအသုံးပြု၍တွက်ချက်သော regression coefficients ၏တန်ဖိုးများမှာ အောက်ပါအတိုင်းဖြစ်သည် ။

$\begin{array}{c}\beta_0\approx -4,1\\[2ex]\beta_1\approx 1,5\end{array}$

ထို့ကြောင့် logistic regression model သည် အောက်ပါအတိုင်းဖြစ်သည် ။

$\begin{aligned}p&=\cfrac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i)}}\\[2ex]p&=\cfrac{1}{1+e^{-(-4,1+1,5x_1)}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\end{aligned}$

အောက်တွင် နမူနာဒေတာနှင့် ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှု စံပြညီမျှခြင်း ဂရပ်ဖစ်ကို ကြည့်ရှုနိုင်သည်-

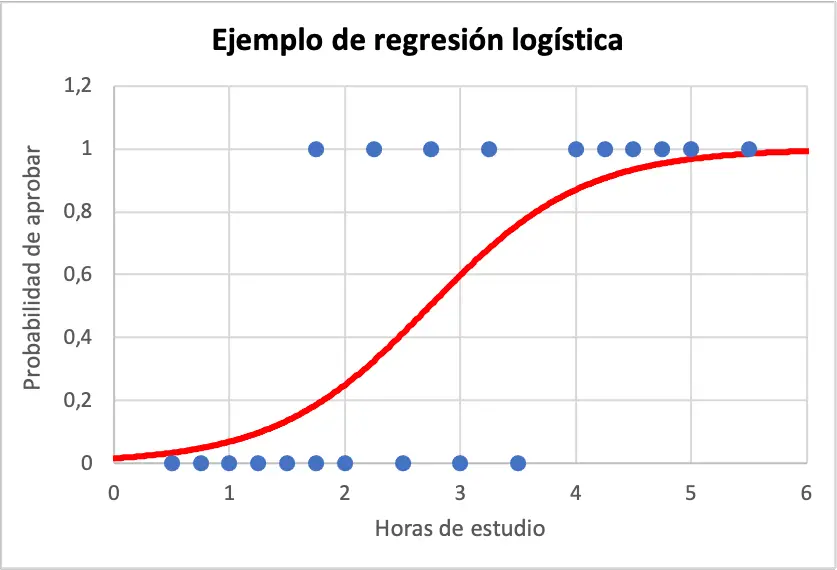
ထို့ကြောင့်၊ ကျောင်းသားတစ်ဦးသည် 4 နာရီစာလေ့လာပါက အောင်မြင်နိုင်ခြေကို တွက်ချက်ရန်၊ logistic regression model မှရရှိသော ညီမျှခြင်းကို ရိုးရိုးရှင်းရှင်းအသုံးပြုပါ။

$\begin{aligned}p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5\cdot 4}}\\[2ex]p&=0,8699\end{aligned}$

အတိုချုပ်ပြောရလျှင် ကျောင်းသားတစ်ဦးသည် လေးနာရီကြာအောင် ဖြေဆိုပါက စာမေးပွဲအောင်ရန် ဖြစ်နိုင်ခြေ 86.99% ရှိမည်ဖြစ်သည်။

Logistic Regression အမျိုးအစားများ

Logistic regression အမျိုးအစား သုံးမျိုးရှိပါတယ်။

Binary Logistic Regression : မှီခို variable သည် တန်ဖိုးနှစ်ခု (0 နှင့် 1) သာရှိနိုင်သည်။
Multinomial logistic regression : မှီခိုကိန်းရှင်တွင် ဖြစ်နိုင်ချေတန်ဖိုး နှစ်ခုထက်ပိုပါသည်။
Ordinal logistic regression : ဖြစ်နိုင်ချေရလဒ်များသည် သဘာဝအတိုင်း ရှိပါသည်။

Logistic regression နှင့် linear regression

နောက်ဆုံးအနေဖြင့်၊ အချုပ်အားဖြင့်၊ စာရင်းဇယားများတွင် အသုံးအများဆုံး ဆုတ်ယုတ်မှုပုံစံမှာ မျဉ်းကြောင်းနမူနာဖြစ်သောကြောင့် ထောက်ပံ့ပို့ဆောင်ရေးဆုတ်ယုတ်မှုနှင့် မျဉ်းကြောင်းပြန်ဆုတ်ခြင်းအကြား ကွာခြားချက်ကို ကျွန်ုပ်တို့တွေ့ရပါမည်။

Linear regression ကို ကိန်းဂဏာန်းမူတည်သော ကိန်းရှင်များကို စံနမူနာပြုရန်အတွက် အသုံးပြုသည်။ ထို့အပြင်၊ linear regression တွင်၊ explanatory variable များနှင့် response variable အကြား ဆက်နွယ်မှုသည် linear ဖြစ်သည်။

ထို့ကြောင့်၊ logistic regression နှင့် linear regression အကြား အဓိကကွာခြားချက် မှာ dependent variable အမျိုးအစားဖြစ်သည်။ ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှုတစ်ခုတွင်၊ မှီခိုကိန်းရှင်သည် အမျိုးအစားအလိုက်ဖြစ်ပြီး၊ မျဉ်းနားဆုတ်ယုတ်မှုတွင် မှီခိုသောကိန်းရှင်သည် ဂဏန်းဖြစ်သည်။

ထို့ကြောင့်၊ လိုက်လျောညီထွေ ဆုတ်ယုတ်မှုအား ကိန်းဂဏာန်းရလဒ်ကို ခန့်မှန်းရာတွင် ဖြစ်နိုင်ခြေရှိသော ရွေးချယ်စရာနှစ်ခုကြားမှ ရလဒ်ကို ခန့်မှန်းရန် အသုံးပြုပါသည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။