နမူနာ ပျမ်းမျှ

အားဖြင့် Benjamin Anderson ဩဂုတ် 3, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် ကိန်းဂဏန်းစာရင်းအင်းနမူနာပျမ်းမျှသည် အဘယ်နည်း။ အလားတူ၊ နမူနာတစ်ခု၏ဆိုလိုအား တွက်ချက်နည်း၊ ဖြေရှင်းထားသော လေ့ကျင့်ခန်းတစ်ခုနှင့်၊ ထို့အပြင် မည်သည့်နမူနာ၏ဆိုလိုသည်ကို တွက်ချက်ရန် အွန်လိုင်းဂဏန်းတွက်စက်ကို သင်တွေ့လိမ့်မည်။

နမူနာဟူသည် အဘယ်နည်း။

ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ နမူနာဆိုလိုသည်မှာ နမူနာတစ်ခုရှိ တန်ဖိုးများ၏ ပျမ်းမျှဖြစ်သည်။ နမူနာဆိုလိုရင်းကို တွက်ချက်ရန်၊ နမူနာရှိ တန်ဖိုးအားလုံးကို ပေါင်းထည့်ပြီးနောက် နမူနာရှိဒေတာ စုစုပေါင်းအရေအတွက်ဖြင့် ပိုင်းခြားရပါမည်။

နမူနာဆိုသည်မှာ သင်္ကေတဖြစ်သည်။

$\overline{x}$

ကိန်းဂဏန်းလေ့လာမှုတစ်ခုတွင် ယေဘုယျအားဖြင့် လူဦးရေ၏တန်ဖိုးအားလုံးကို မသိရသောကြောင့် ၎င်းကိုခွဲခြမ်းစိတ်ဖြာရန် လူဦးရေနမူနာတစ်ခုကို ရွေးချယ်ကာ လူဦးရေတစ်ခုလုံးအတွက်ရရှိသော ကောက်ချက်များအား ပေါင်းထည့်ခြင်းဖြစ်သည်။ ထို့ကြောင့် နမူနာဆိုလိုသည် လူဦးရေကို ခန့်မှန်းရန် အသုံးပြုသည်။

ပျမ်းမျှဖော်မြူလာနမူနာ

နမူနာဆိုလိုသည်မှာ နမူနာအရွယ်အစားဖြင့် ပိုင်းခြားထားသော နမူနာတန်ဖိုးများအားလုံး၏ ပေါင်းလဒ်နှင့် ညီမျှသည်။ ဆိုလိုသည်မှာ၊ နမူနာဆိုလိုချက်ကို တွက်ချက်ရန်၊ နမူနာရှိတန်ဖိုးအားလုံးကို ပေါင်းထည့်ပြီးနောက် နမူနာရှိဒေတာစုစုပေါင်းအရေအတွက်ဖြင့် ပိုင်းခြားခြင်းဖြစ်သည်။

ထို့ကြောင့် နမူနာဆိုလိုအား တွက်ချက်ရန် ဖော်မြူလာ မှာ-

$\displaystyle\overline{x}=\frac{\displaystyle \sum_{i=1}^n x_i}{n}=\frac{x_1+x_2+\dots +x_n}{n}$

👉 မည်သည့်ဒေတာအစုံ၏နမူနာဆိုလိုချက်ကို တွက်ချက်ရန် အောက်ပါ ဂဏန်းပေါင်းစက်ကို သင်အသုံးပြုနိုင်ပါသည်။

နမူနာဆိုလိုရင်းကို နမူနာတစ်ခုမှဒေတာကိုအသုံးပြု၍ တွက်ချက်ကြောင်း မှတ်သားထားပါ၊ ထို့ကြောင့် လူဦးရေ၏ဆိုလိုရင်းတန်ဖိုးသည် တွက်ချက်ထားသောတန်ဖိုးနှင့် ကွာခြားနိုင်သည်ကို သတိရပါ။

နမူနာ Mean တွက်ချက်မှု နမူနာ

ယခု နမူနာဆိုလိုချက်၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ၎င်း၏ဖော်မြူလာသည် မည်ကဲ့သို့ဖြစ်သည်ကို ကျွန်ုပ်တို့သိရှိပြီး ရိုးရှင်းသောနမူနာကိုဖြေရှင်းခြင်းဖြင့် ဒေတာသတ်မှတ်ထားသောနမူနာကို မည်သို့ရယူရမည်ကို ကြည့်ကြပါစို့။

Jose သည် မြို့လယ်ခေါင်သို့ ပြောင်းရွှေ့လိုသော်လည်း သူ့တွင် အချိန်သိပ်မရှိသောကြောင့် ငှားရန်ရှိသော တိုက်ခန်းများ၏ စျေးနှုန်းများကို မခွဲခြမ်းစိတ်ဖြာနိုင်ပါ။ ထို့ကြောင့် သင်သည် မြို့လယ်တွင် နေထိုင်ရန် မည်မျှကုန်ကျမည်ကို သိရှိရန် တိုက်ခန်းငါးခန်း၏ ငှားရမ်းခစျေးနှုန်းကိုသာ ကြည့်ရန် ဆုံးဖြတ်လိုက်ပါသည်။ နမူနာ၏ပျမ်းမျှစျေးနှုန်းကဘာလဲ။

€600 €430 €820 €575 €950

နမူနာဆိုလိုချက်ကို ရှာရန်၊ ကျွန်ုပ်တို့သည် နမူနာတန်ဖိုးများအားလုံးကို ပေါင်းထည့်ရန် လိုအပ်ပြီး စုစုပေါင်း လေ့လာသုံးသပ်ချက်အရေအတွက်အားဖြင့် 5 ဖြစ်သည့် 5 ဖြစ်သောကြောင့်၊ နမူနာဆိုလိုပုံသေနည်းကို ကျွန်ုပ်တို့အသုံးပြုသည်-

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}=\frac{x_1+x_2+x_3+x_4+x_5}{n}$

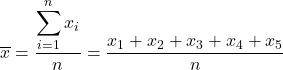
ထို့နောက်၊ ကျွန်ုပ်တို့သည် ဒေတာကို ဖော်မြူလာတွင် အစားထိုးပြီး နမူနာ ဆိုလိုချက်ကို တွက်ချက်သည်-

$\overline{x}=\cfrac{600+430+820+575+950}{5}=675$

အတိုချုပ်အားဖြင့်၊ နမူနာအတွက် ရွေးချယ်ထားသော တိုက်ခန်းများ၏ ပျမ်းမျှစျေးနှုန်းမှာ ယူရို ၆၇၅ ဖြစ်သည်။

ပျမ်းမျှဂဏန်းတွက်စက် ဥပမာ

၎င်း၏နမူနာဆိုလိုရင်းကို တွက်ချက်ရန် အောက်ဖော်ပြပါ ဂဏန်းပေါင်းစက်ထဲသို့ မည်သည့် ကိန်းဂဏန်းနမူနာမှ ဒေတာကို ထည့်သွင်းပါ။ ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။

နမူနာဆိုလိုချက် လူဦးရေဆိုလိုသည်။

လူဦးရေ ပျမ်းမျှ သည် စာရင်းအင်းလူဦးရေ၏ ပျမ်းမျှဖြစ်သည်။ ထို့ကြောင့် လူဦးရေပျမ်းမျှသည် စာရင်းအင်းလေ့လာမှုတစ်ခုပြုလုပ်ရန် ရည်ရွယ်ထားသည့် အစိတ်အပိုင်းအားလုံး၏ပျမ်းမျှဖြစ်သည်။

ထို့ကြောင့် နမူနာဆိုလိုရင်းနှင့် လူဦးရေဆိုလိုရင်းအကြား ကွာခြားချက် မှာ နမူနာဆိုလိုသည်မှာ နမူနာတန်ဖိုးများ၏ ပျမ်းမျှဖြစ်ပြီး လူဦးရေဆိုလိုသည်မှာ လူဦးရေအတွက် ပျမ်းမျှတန်ဖိုးများဖြစ်သည်။

နမူနာဆိုလိုအား လူဦးရေဆိုလိုရင်းနှင့် ကွဲပြားစေရန်၊ ၎င်းတို့ကို မတူညီသောသင်္ကေတများဖြင့် ကိုယ်စားပြုပါသည်။ နမူနာဆိုသည်မှာ သင်္ကေတဖြစ်သည်။

$\overline{x}$

လူဦးရေအတွက် သင်္ကေတဟု အဓိပ္ပါယ်ရသည်။

$\mu$

$\begin{array}{c}\overline{x} = \text{Media muestral}\\[2ex]\mu =\text{Media poblacional}\end{array}$

ပွိုင့် ခန့်မှန်းချက် သို့မဟုတ် ကြားကာလ ခန့်မှန်းချက် ကို အသုံးပြု၍ လုပ်ဆောင်နိုင်သည့် လူဦးရေ ပျမ်းမျှတန်ဖိုးကို ခန့်မှန်းရန် နမူနာဆိုလိုအား အသုံးပြုသည်။

➤ ကြည့်ပါ- လူဦးရေ ပျမ်းမျှက ဘယ်လောက်လဲ။

နမူနာ ဖြန့်ဖြူးခြင်း နမူနာကို ဆိုလိုသည်။

နောက်ဆုံးတွင်၊ နမူနာ၏နမူနာဖြန့်ဝေမှုသည် ရှုပ်ထွေးစေမည့် ကိန်းဂဏန်းအယူအဆတစ်ခုဖြစ်သောကြောင့် လေ့လာကြည့်ကြပါစို့။

ဦးစွာ၊ နမူနာဖြန့်ချီခြင်းဆိုသည်မှာ မည်သည်ကို သတ်မှတ်ခြင်းဖြင့် စတင်ကြပါစို့။ နမူနာဖြန့်ဝေခြင်း ဆိုသည်မှာ ကိန်းဂဏန်းလူဦးရေတစ်ခုမှ ဖြစ်နိုင်သောနမူနာအားလုံးကို ထည့်သွင်းတွက်ချက်ခြင်းမှ ထွက်ပေါ်လာသော ဖြန့်ဝေမှုဖြစ်သည်။

ထို့ကြောင့်၊ နမူနာဆိုလိုမှု၏နမူနာဖြန့်ဝေမှုသည် လူဦးရေတစ်ခုမှဖြစ်နိုင်သောနမူနာတစ်ခုစီ၏ပျမ်းမျှအား တွက်ချက်ခြင်းမှရရှိလာသော ဖြန့်ဖြူးမှုဖြစ်သည်။ ဆိုလိုသည်မှာ၊ ကျွန်ုပ်တို့သည် လူဦးရေတစ်ခုမှ ဖြစ်နိုင်သောနမူနာအားလုံးကို လေ့လာပြီး နမူနာတစ်ခုစီ၏ ဆိုလိုရင်းကို တွက်ချက်ပါက၊ တွက်ချက်ထားသော တန်ဖိုးများအစုသည် နမူနာဆိုလိုမှု၏ နမူနာဖြန့်ဝေမှုတစ်ခုဖြစ်သည်။

နိဂုံးချုပ်အားဖြင့်၊ နမူနာဆိုလိုရင်းနှင့် နမူနာဖြန့်ဝေမှုတွင် ဆင်တူသောအမည်များ ရှိသော်လည်း ၎င်းတို့ကို ခွဲခြားသိရန် လိုအပ်သည်- နမူနာဆိုလိုသည်မှာ နမူနာတစ်ခုမှ တွက်ချက်ထားသည့် ကိန်းဂဏန်းသတ်မှတ်ချက်တစ်ခုဖြစ်ပြီး အခြားတစ်ဖက်တွင်၊ နမူနာဖြန့်ချီမှုသည် ဖြန့်ဖြူးမှုတစ်ခုဖြစ်သည်။ ၎င်းသည် လူဦးရေမှ ပြုလုပ်နိုင်သော နမူနာများအားလုံးကို လေ့လာခြင်းမှ ရလဒ်ဖြစ်သည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။