နမူနာဖြန့်ဝေခြင်းဆိုသည်မှာ အဘယ်နည်း။

လူဦးရေ 10,000 ရှိသော လင်းပိုင်များ ရှိနေပြီး ထိုလူဦးရေတွင် လင်းပိုင်၏ ပျမ်းမျှအလေးချိန်မှာ ပေါင် 300 ဖြစ်သည်။

ဤလူဦးရေမှ လင်းပိုင် ၅၀ ၏ ရိုးရှင်းသောကျပန်းနမူနာကို ယူပါက၊ ဤနမူနာတွင် လင်းပိုင်၏ပျမ်းမျှအလေးချိန်မှာ 305 ပေါင်ဖြစ်ကြောင်း တွေ့ရှိနိုင်သည်။

ထို့နောက် လင်းပိုင် ၅၀ ၏ ရိုးရှင်းသော ကျပန်းနမူနာကို ယူပါက၊ ဤနမူနာရှိ လင်းပိုင်၏ ပျမ်းမျှအလေးချိန်မှာ ၂၉၅ ပေါင်ဖြစ်ကြောင်း တွေ့ရှိနိုင်သည်။

လင်းပိုင် 50 ၏ ရိုးရှင်းသော ကျပန်းနမူနာကို ယူသည့်အခါတိုင်း၊ နမူနာရှိ လင်းပိုင်၏ ပျမ်းမျှအလေးချိန်သည် လူဦးရေ ပျမ်းမျှ ပေါင် 300 နှင့် နီးစပ်သော်လည်း ပေါင် 300 အတိအကျမဟုတ်ပေ။

ဤလူဦးရေထဲမှ လင်းပိုင် ၅၀ ၏ ရိုးရှင်းသောကျပန်းနမူနာ ၂၀၀ ကိုယူကာ နမူနာတစ်ခုစီ၏ ပျမ်းမျှအလေးချိန်၏ ဟီစတိုဂရမ်တစ်ခုကို ဖန်တီးကြည့်ကြပါစို့။

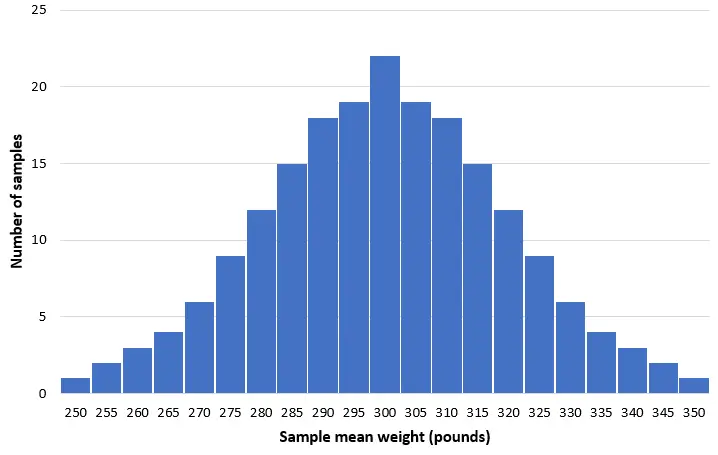
နမူနာအများစုတွင် ပျမ်းမျှအလေးချိန်သည် ပေါင် ၃၀၀ နီးပါးရှိမည်ဖြစ်သည်။ ရှားပါးသောကိစ္စများတွင်၊ ကျွန်ုပ်တို့သည် ပျမ်းမျှအလေးချိန် ပေါင် 250 သာရှိသော လင်းပိုင်ငယ်လေးများနှင့် ပြည့်နေသောနမူနာကို ယူနိုင်သည်။ သို့မဟုတ် ပျမ်းမျှအားဖြင့် ပေါင် 350 ရှိသော နှာဘူး လင်းပိုင်များ အပြည့်နမူနာကို ယူနိုင်သည်။ ယေဘူယျအားဖြင့်၊ နမူနာနည်းလမ်းများ ဖြန့် ဖြူးမှုသည် ခန့်မှန်းခြေအားဖြင့် ပုံမှန်ဖြစ်ပြီး၊ ဖြန့်ဖြူးမှု၏ဗဟိုသည် လူဦးရေ၏ဗဟိုချက်အမှန်တွင်တည်ရှိသည်။

ဤနမူနာ၏ ဖြန့်ဖြူးခြင်းနည်းလမ်းကို ဆိုလို ခြင်း၏နမူနာဖြန့်ဝေမှု ဟု လူသိများပြီး အောက်ပါဂုဏ်သတ္တိများ ရှိသည်။

_µx = µ

µ _x သည် နမူနာဆိုလိုပြီး μ သည် လူဦးရေဆိုလိုသည်။

_σx = σ/√n

σ _x သည် နမူနာစံသွေဖည်သည့်နေရာတွင်၊ σ သည် လူဦးရေစံသွေဖည်ဖြစ်ပြီး n သည် နမူနာအရွယ်အစားဖြစ်သည်။

ဥပမာအားဖြင့်၊ ဤလင်းပိုင်များ၏လူဦးရေတွင်၊ ပျမ်းမျှအလေးချိန်မှာ μ = 300 ဖြစ်ကြောင်း ကျွန်ုပ်တို့သိပါသည်။ ထို့ကြောင့် နမူနာဖြန့်ဝေမှု၏ပျမ်းမျှမှာ μ _x = 300 ဖြစ်သည်။

လူဦးရေစံသွေဖည်မှုမှာ 18 ပေါင်ဖြစ်သည်ဆိုပါစို့။ ထို့ကြောင့် နမူနာစံသွေဖည်မှုသည် σ _x = 18/ √50 = 2.546 ဖြစ်သည်။

အချိုးအစားနမူနာ ဖြန့်ဝေခြင်း။

တူညီသောလူဦးရေ 10,000 လင်းပိုင်စဉ်းစားပါ။ လင်းပိုင်များ၏ 10% သည် အနက်ရောင်ဖြစ်ပြီး ကျန်များမှာ မီးခိုးရောင်ဟု ယူဆပါ။ ကျွန်ုပ်တို့သည် လင်းပိုင် ၅၀ ၏ ရိုးရှင်းသော ကျပန်းနမူနာကို ယူကာ ထိုနမူနာရှိ လင်းပိုင်များ၏ 14% သည် အနက်ရောင်ဖြစ်သည်ဆိုပါစို့။ ထို့နောက်၊ ကျွန်ုပ်တို့သည် လင်းပိုင် ၅၀ ၏ ရိုးရှင်းသော ကျပန်းနမူနာကို ယူကာ ဤနမူနာရှိ လင်းပိုင်များ၏ ၈ ရာခိုင်နှုန်းသည် အနက်ရောင်ဖြစ်ကြောင်း တွေ့ရှိရသည်။

ဤလူဦးရေမှ လင်းပိုင် ၅၀ ၏ ရိုးရှင်းသောကျပန်းနမူနာ ၂၀၀ ကိုယူကာ နမူနာတစ်ခုစီရှိ လင်းပိုင်နက်များ၏ အချိုးအစား၏ histogram တစ်ခုကို ဖန်တီးရန် စိတ်ကူးကြည့်ပါ-

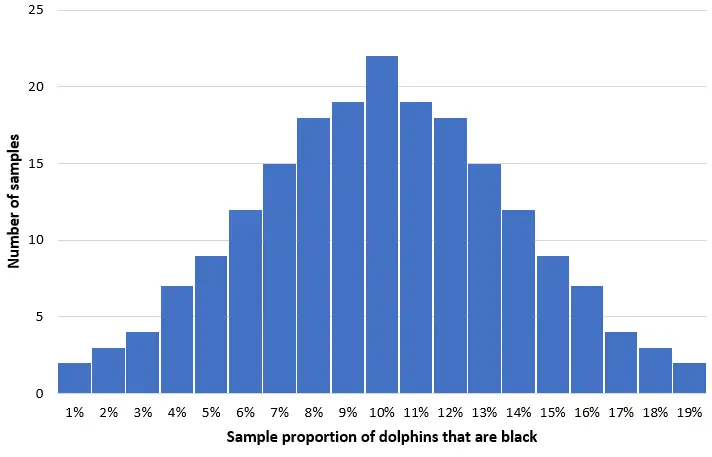
နမူနာအများစုတွင် လင်းပိုင်နက်များ၏ အချိုးအစားသည် အမှန်တကယ် လူဦးရေ၏ 10% နှင့် နီးစပ်မည်ဖြစ်သည်။ လင်းပိုင်နက်၏နမူနာအချိုးအစား ဖြန့် ဝေမှုသည် ခန့်မှန်းခြေအားဖြင့် ပုံမှန်ဖြစ်လိမ့်မည်၊ ဖြန့်ဖြူးမှု၏ဗဟိုသည် လူဦးရေ၏ဗဟိုချက်အမှန်တွင်တည်ရှိသည်။

ဤနမူနာအချိုးအစားများ ဖြန့်ဝေခြင်းကို အချိုးအစားနမူနာဖြန့်ဝေခြင်း ဟု လူသိများပြီး အောက်ပါဂုဏ်သတ္တိများ ရှိသည်။

_µp = P

p သည် နမူနာအချိုးဖြစ်ပြီး P သည် လူဦးရေအချိုးဖြစ်သည်။

σ _p = √ (P)(1-P) / n

P သည် လူဦးရေအချိုးအစားဖြစ်ပြီး n သည် နမူနာအရွယ်အစားဖြစ်သည်။

ဥပမာအားဖြင့်၊ ဤလင်းပိုင်လူဦးရေတွင် လင်းပိုင်နက်၏ အချိုးအစားအမှန်မှာ 10% = 0.1 ဖြစ်သည်ကို ကျွန်ုပ်တို့သိပါသည်။ ထို့ကြောင့်၊ အချိုးနမူနာဖြန့်ဝေမှု၏ပျမ်းမျှသည် μ _p = 0.1 ဖြစ်သည်။

လူဦးရေစံသွေဖည်မှုမှာ 18 ပေါင်ဖြစ်သည်ဆိုပါစို့။ ထို့ကြောင့် နမူနာစံသွေဖည်မှုသည် σ _p = √ (P)(1-P) / n = √ (.1)(1-.1) / 50 = .042 ဖြစ်သည်။

ပုံမှန်အနေအထားကို ထူထောင်ပါ။

အထက်ဖော်ပြပါ ဖော်မြူလာများကို အသုံးပြုရန်၊ နမူနာဖြန့်ဝေမှုသည် ပုံမှန်ဖြစ်ရပါမည်။

ဗဟိုကန့်သတ်သီအိုရီ အရ၊ လူဦးရေခွဲဝေမှုမှာ ပုံမှန်မဟုတ်သော်လည်း နမူနာအရွယ်အစားသည် ပုံမှန်မဟုတ်သော်လည်း နမူနာအတိုင်းအတာတစ်ခု၏နမူနာဖြန့်ဝေမှုသည် ခန့်မှန်းခြေအားဖြင့် ပုံမှန်ဖြစ်သည် ။ ကိစ္စအများစုတွင်၊ နမူနာအရွယ်အစား 30 သို့မဟုတ် ထို့ထက်ပို၍ ကြီးမားသည်ဟု ကျွန်ုပ်တို့ယူဆပါသည်။

မျှော်မှန်းထားသော အောင်မြင်မှု နှင့် ကျရှုံးမှု အရေအတွက် အနည်းဆုံး 10 နှစ်ခုလုံးသည် မျှော်မှန်းထားသည့် အောင်မြင်မှု နှင့် ကျရှုံးမှု နှစ်ခုလုံးတွင် နမူနာအချိုးတစ်ခု၏ နမူနာဖြန့်ဝေမှုသည် ခန့်မှန်းခြေအားဖြင့် ပုံမှန်ဖြစ်သည်။

ဥပမာများ

ဖြစ်နိုင်ခြေများကို တွက်ချက်ရန် နမူနာဖြန့်ဝေမှုများကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။

ဥပမာ 1- အချို့သောစက်သည် ကွတ်ကီးများကို ဖန်တီးသည်။ ဤ cookies များ၏ အလေးချိန် ဖြန့်ဖြူးမှုကို ပျမ်းမျှ 10 အောင်စနှင့် စံသွေဖည်မှု 2 အောင်စဖြင့် ညာဘက်သို့ လှည့်သည်။ ဤစက်မှထုတ်လုပ်သော ကွတ်ကီး 100 ၏ ရိုးရှင်းသောကျပန်းနမူနာကို ယူပါက၊ ဤနမူနာရှိ ကွတ်ကီးများ၏ ပျမ်းမျှအလေးချိန်သည် 9.8 အောင်စထက်နည်းသော ဖြစ်နိုင်ခြေရှိသနည်း။

အဆင့် 1- ပုံမှန်အနေအထားကို ထူထောင်ပါ။

နမူနာနည်းလမ်းများ ၏နမူနာဖြန့်ဝေမှုသည် ပုံမှန်ဖြစ်ကြောင်း သေချာစေရန် လိုအပ်ပါသည်။ ကျွန်ုပ်တို့၏နမူနာအရွယ်အစားသည် 30 ထက်ကြီးသည် သို့မဟုတ် ညီမျှသောကြောင့်၊ ဗဟိုကန့်သတ်သီအိုရီအရ၊ နမူနာ၏နမူနာဖြန့်ဝေမှုသည် ပုံမှန်ဖြစ်သည်ဟု ကျွန်ုပ်တို့ယူဆနိုင်သည်။

အဆင့် 2- နမူနာဖြန့်ဝေမှု၏ ပျမ်းမျှနှင့် စံသွေဖည်မှုကို ရှာပါ။

_µx = µ

_σx = σ/√n

μ _x = 10 အောင်စ

σ _x = 2/ √100 = 2/10 = 0.2 အောင်စ

အဆင့် 3- ဤနမူနာရှိ ပျမ်းမျှ cookie အလေးချိန်သည် 9.8 အောင်စထက်နည်းသည်ဟု ဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ရန် Z-Score ဧရိယာဂဏန်းတွက်စက်ကို အသုံးပြုပါ။

Z Score Area Calculator တွင် အောက်ပါနံပါတ်များကို ထည့်ပါ။ ဤဥပမာတွင် နံပါတ်တစ်ခုသာတွေ့သောကြောင့် “ Raw Score 2” ကို ဗလာချန်ထားနိုင်ပါသည်။

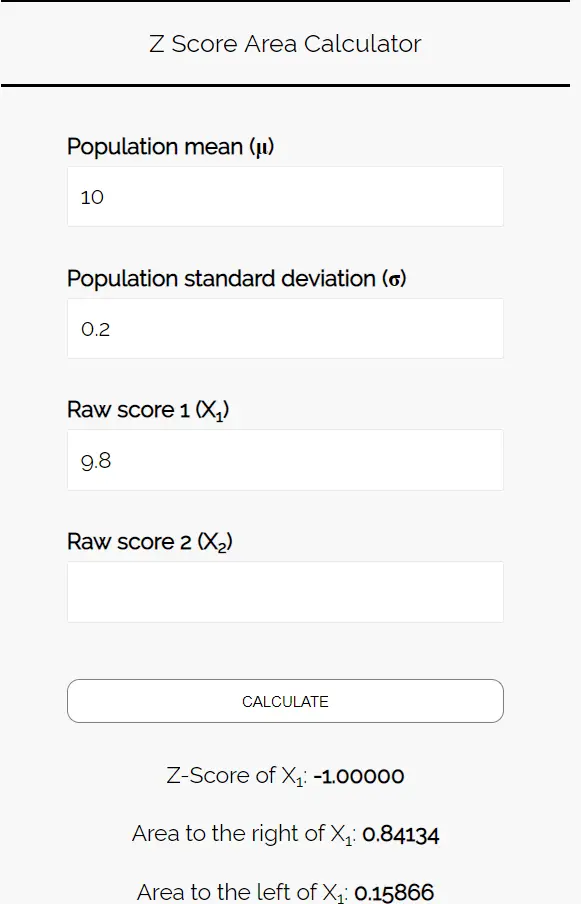
ဤနမူနာရှိ cookies များ၏ ပျမ်းမျှအလေးချိန်သည် 9.8 အောင်စ ထက်နည်းသော ဖြစ်နိုင်ခြေကို သိရှိလိုသောကြောင့်၊ ဘယ်ဘက် ရှိ 9.8 ဧရိယာကို ကျွန်ုပ်တို့ စိတ်ဝင်စားပါသည်။ ဂဏန်းပေါင်းစက်က ဤဖြစ်နိုင်ခြေသည် 0.15866 ဖြစ်ကြောင်း ကျွန်တော်တို့ကို ပြောပြသည်။

ဥပမာ 2- ကျောင်းတစ်ကျောင်းလုံး လေ့လာမှုတစ်ခုအရ၊ ကျောင်းရှိ ကျောင်းသား 87% သည် ပီဇာကို ရေခဲမုန့်ကို နှစ်သက်သည်။ ကျွန်ုပ်တို့သည် ကျောင်းသား ၂၀၀ ၏ ရိုးရှင်းသော ကျပန်းနမူနာကို ယူသည်ဆိုပါစို့။ ပီဇာနှစ်သက်သော ကျောင်းသားများ၏ အချိုးသည် 85% အောက် ဖြစ်နိုင်ခြေ မည်မျှရှိသနည်း။

အဆင့် 1- ပုံမှန်အနေအထားကို ထူထောင်ပါ။

“ အောင်မြင်မှုများ” နှင့် “ ကျရှုံးမှုများ” နှစ်ခုစလုံးသည် အနည်းဆုံး 10 ဖြစ်သည်ဆိုပါက နမူနာအချိုးတစ်ခု၏နမူနာဖြန့်ဝေမှုသည် ခန့်မှန်းခြေအားဖြင့် ပုံမှန်ဖြစ်ကြောင်း သတိရပါ။

ဤကိစ္စတွင်၊ ပီဇာနှစ်သက်မည့် ကျောင်းသားဦးရေမှာ 87% * 200 ကျောင်းသား = 174 ကျောင်းသားဖြစ်သည်။ ပီဇာကို မကြိုက်သော ကျောင်းသားဦးရေ မျှော်မှန်းထားသည်မှာ 13% * 200 ကျောင်းသား = 26 ကျောင်းသား။ ဤကိန်းဂဏန်းနှစ်ခုလုံးသည် အနည်းဆုံး 10 ဖြစ်သောကြောင့်၊ ပီဇာကြိုက်မည့် ကျောင်းသားများ၏ အချိုးအစားနမူနာဖြန့်ဝေမှုသည် ခန့်မှန်းခြေအားဖြင့် ပုံမှန်ဖြစ်သည်ဟု ကျွန်ုပ်တို့ ယူဆနိုင်ပါသည်။

အဆင့် 2- နမူနာဖြန့်ဝေမှု၏ ပျမ်းမျှနှင့် စံသွေဖည်မှုကို ရှာပါ။

_µp = P

σ _p = √ (P)(1-P) / n

_µp = 0.87

σ _p = √ (0.87)(1-0.87) / 200 = 0.024

အဆင့် 3- ပီဇာနှစ်သက်သော ကျောင်းသားများ၏ အချိုးသည် 85% အောက်ဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ရန် Z-Score ဧရိယာဂဏန်းတွက်စက်ကို အသုံးပြုပါ။

Z Score Area Calculator တွင် အောက်ပါနံပါတ်များကို ထည့်ပါ။ ဤဥပမာတွင် နံပါတ်တစ်ခုသာတွေ့သောကြောင့် “ Raw Score 2” ကို ဗလာချန်ထားနိုင်ပါသည်။

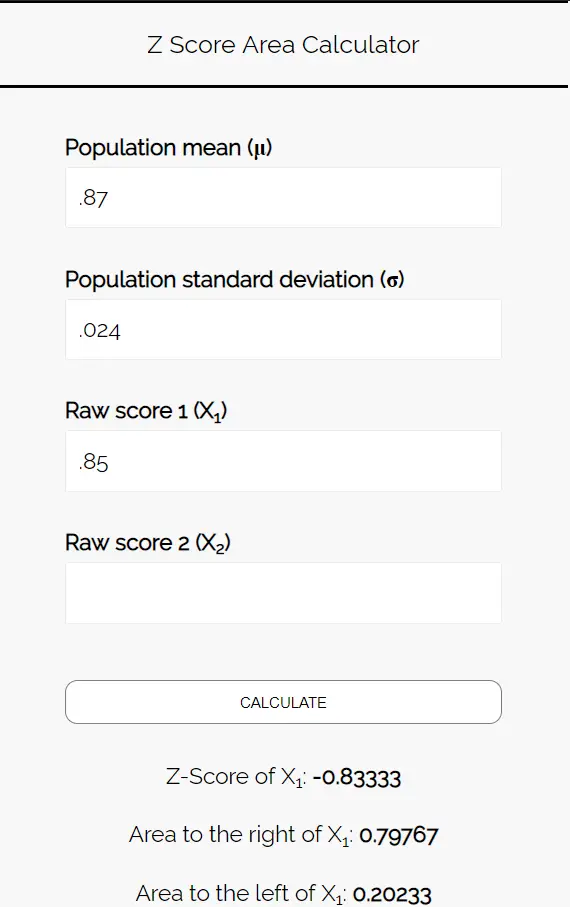
ပီဇာနှစ်သက်သော ကျောင်းသားများ၏ အချိုးသည် 85% ထက်နည်းသော ဖြစ်နိုင်ခြေကို သိရှိလိုသောကြောင့် 0.85 ၏ ဘယ်ဘက် ရှိ ဧရိယာကို ကျွန်ုပ်တို့ စိတ်ဝင်စားပါသည်။ ဂဏန်းပေါင်းစက်က ဤဖြစ်နိုင်ခြေသည် 0.20233 ဖြစ်ကြောင်း ကျွန်တော်တို့ကို ပြောပြသည်။