နမူနာအချိုး

အားဖြင့် Benjamin Anderson ဩဂုတ် 3, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် စာရင်းအင်းကိန်းဂဏန်းနမူနာအချိုးသည် အဘယ်အရာကို ရှင်းပြထားသည်။ ထို့ကြောင့်၊ နမူနာအချိုးအစား၊ ဖြေရှင်းထားသော လေ့ကျင့်ခန်းတစ်ခုနှင့် နမူနာအချိုးအစားနှင့် လူဦးရေအချိုးအကြား ကွာခြားချက်က မည်ကဲ့သို့ ကွာခြားသည်ကို သင်ရှာဖွေတွေ့ရှိမည်ဖြစ်သည်။

နမူနာအချိုးက ဘယ်လောက်လဲ။

နမူနာအချိုး သည် နမူနာတစ်ခုရှိ အောင်မြင်သောကိစ္စများ၏ အချိုးအစားနှင့် နမူနာအရွယ်အစားဖြစ်သည်။ ထို့ကြောင့် နမူနာအချိုးအစားကို တွက်ချက်ရန်၊ နမူနာတွင် အောင်မြင်မှုအရေအတွက်ကို စုစုပေါင်းဒေတာအရေအတွက်ဖြင့် ပိုင်းခြားရပါမည်။

နမူနာအချိုးအတွက် သင်္ကေတသည်

$\widehat{p}$

စာရင်းဇယားများတွင်၊ စစ်တမ်းတစ်ခုပြုလုပ်သောအခါတွင် လူဦးရေဒေတာအားလုံးကို အများအားဖြင့်မသိရသောကြောင့် ကိုယ်စားလှယ်နမူနာတစ်ခု၏လေ့လာမှုကို အများအားဖြင့်လုပ်ဆောင်ကြပြီး၊ ထို့နောက်ကောက်ချက်ဆွဲမှုများကို ပြည်သူတစ်ရပ်လုံးသို့ ခွဲထုတ်ပါသည်။ လူဦးရေ။ ထို့ကြောင့် နမူနာအချိုးကို လူဦးရေတစ်ခုလုံး၏အချိုးအစား ခန့်မှန်းရန်အသုံးပြုသည်။ အောက်တွင် ကျွန်ုပ်တို့ မည်သို့လုပ်ဆောင်သည်ကို တွေ့ရမည်ဖြစ်ပါသည်။

➤ ကြည့်ပါ- ကိုယ်စားလှယ်နမူနာများကား အဘယ်နည်း။

အချိုးအစားဖော်မြူလာနမူနာ

နမူနာအချိုးသည် နမူနာအရွယ်အစားဖြင့် ပိုင်းခြားထားသော နမူနာရှိ အောင်မြင်သော အမှုအရေအတွက်နှင့် ညီမျှသည်။ ထို့ကြောင့်၊ နမူနာအချိုးကို တွက်ချက်ရန် ဖော်မြူလာ မှာ-

$\widehat{p}=\cfrac{e}{n}$

ရွှေ-

$\widehat{p}$

နမူနာအချိုးဖြစ်သည်။
$e$

နမူနာတွင် အောင်မြင်သော အမှုအရေအတွက်ဖြစ်သည်။
$n$

နမူနာရှိ အချက်အလက် စုစုပေါင်း အရေအတွက် ဖြစ်သည် ။

နမူနာ အချိုးအစား တွက်ချက်ခြင်း ဥပမာ

နမူနာအချိုးအစား၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ၎င်း၏ဖော်မြူလာသည် မည်ကဲ့သို့ဖြစ်သည်ကို ကြည့်ပြီးနောက်၊ ဤအပိုင်းတွင် နမူနာအချိုးကို တွက်ချက်ပုံကို သင်ကြည့်ရှုနိုင်စေရန် ရိုးရှင်းသော ဥပမာတစ်ခုကို ဖြေရှင်းပါမည်။

ကုမ္ပဏီတစ်ခုသည် အရုပ်တစ်ခုထုတ်လုပ်ပြီး အခြားပြင်ပကုမ္ပဏီတစ်ခုထံမှ ၎င်း၏အစိတ်အပိုင်းတစ်ခုကို ဝယ်ယူသည်။ သို့သော် သူဝယ်ယူသည့်အသုတ်များတွင် ချွတ်ယွင်းသောအစိတ်အပိုင်းများ ပေါ်လာသဖြင့် အခြေအနေကောင်းနှင့် ချို့ယွင်းချက်အချိုးအစားကို သိရှိရန် ကိန်းဂဏန်းလေ့လာမှုတစ်ရပ်ကို လုပ်ဆောင်ရန် ဆုံးဖြတ်ခဲ့သည်။ ထို့ကြောင့်၊ သင်သည် ယူနစ် ၁၀၀၀ ၏နမူနာကို မှာယူကာ ချို့ယွင်းနေသော အစိတ်အပိုင်း ၁၃၈ ခုကို ရှာဖွေပါ။ နမူနာတွင် ကောင်းမွန်သော အခြေအနေရှိ အစိတ်အပိုင်းများ၏ အချိုးအစားသည် အဘယ်နည်း။ နမူနာမှာ ချို့ယွင်းနေတဲ့ အစိတ်အပိုင်းတွေရဲ့ အချိုးအစားက ဘယ်လောက်လဲ။

နမူနာရှိ မပျက်စီးသော အစိတ်အပိုင်း အရေအတွက်သည် 1000 အနှုတ် ချို့ယွင်းနေသော အစိတ်အပိုင်းများ ဖြစ်သည်-

$e=1000-138=862$

ထို့ကြောင့်၊ နမူနာအချိုးကိုရှာရန်၊ အထက်တွင်တွေ့မြင်ရသော ဖော်မြူလာကို အသုံးပြုပါ။

$\widehat{p}=\cfrac{e}{n}=\cfrac{862}{1000}=0,862$

ထို့ကြောင့် အခြေအနေကောင်းရှိ အစိတ်အပိုင်းများ၏ နမူနာအချိုးသည် 86.2% ဖြစ်သည်။

အခြားတစ်ဖက်တွင်၊ ချို့ယွင်းနေသော အစိတ်အပိုင်းများ၏ အချိုးအစားသည် ကောင်းမွန်သော အစိတ်အပိုင်းများ၏ အချိုးအနုတ်တစ်ခုနှင့် ညီမျှသည်-

$\widehat{q}=1-\widehat{p}=1-0,862=0,138$

ထို့ကြောင့် ချို့ယွင်းနေသော အစိတ်အပိုင်းများ၏ နမူနာအချိုးသည် 13.8% ဖြစ်သည်။

နမူနာအချိုးနှင့် လူဦးရေအချိုး

လူဦးရေအချိုး သည် စာရင်းအင်းလူဦးရေအချိုးအစားဖြစ်သည်။ ဆိုလိုသည်မှာ လူဦးရေအချိုးအစားသည် လူဦးရေ၏ အစိတ်အပိုင်းအားလုံးနှင့် ဆက်စပ်လေ့လာထားသော လူဦးရေ၏ အောင်မြင်မှုဆိုင်ရာ ဆက်စပ်မှုဖြစ်သည်။

ထို့ကြောင့် အမျိုးသားအချိုးအစားနှင့် လူဦးရေအချိုးအကြား ကွာခြားချက် မှာ အမျိုးသားအချိုးအစားသည် လူများစု၏ အချိုးအစားဖြစ်ပြီး အပြောင်းအလဲတွင် လူဦးရေအချိုးသည် လူဦးရေဆိုင်ရာ အစိတ်အပိုင်းအားလုံးနှင့် သက်ဆိုင်သည့် ဖြစ်ရပ်များ၏ အချိုးအစားကို ရည်ညွှန်းပါသည်။

လူဦးရေအချိုးအစားနမူနာအချိုးကို ခွဲခြားရန်၊ ၎င်းတို့ကို မတူညီသောသင်္ကေတများဖြင့် ကိုယ်စားပြုသည်။ နမူနာအချိုးအတွက် သင်္ကေတသည်

$\widehat{p}$

လူဦးရေအချိုးအစား သင်္ကေတသည် ၊

$p$

ယေဘူယျအားဖြင့် လူဦးရေအချိုးအစားကို အတိအကျ မဆုံးဖြတ်နိုင်သောကြောင့် လူဦးရေတန်ဖိုးအားလုံးကို အများအားဖြင့် မသိကြပါ။ ယင်းအစား၊ လူဦးရေအချိုးအစားတန်ဖိုးကို အောက်ပါဖော်မြူလာဖြင့် ယုံကြည်ချက်ကြားကာလကို အသုံးပြု၍ ခန့်မှန်းတွက်ချက်သည်-

$\displaystyle \left(\widehat{p}-Z_{\alpha/2}\sqrt{\frac{\widehat{p}(1-\widehat{p})}{n}}\ , \ \widehat{p}+Z_{\alpha/2}\sqrt{\frac{\widehat{p}(1-\widehat{p})}{n}}\right)$

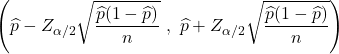
လူဦးရေအချိုးကို ခန့်မှန်းကြည့်ရန် အောက်ပါလင့်ခ်ကို နှိပ်ပါ။

➤ လူဦးရေအချိုးအတွက် ယုံကြည်မှုကြားကာလကို ကြည့်ပါ။

အချိုးအစားနမူနာ ဖြန့်ဝေခြင်း။

နောက်ဆုံးတွင်၊ အချိုးအစားနမူနာခွဲဝေမှုတွင် မည်သည့်အရာပါဝင်သည်ကို ကျွန်ုပ်တို့တွေ့မြင်ရမည်ဖြစ်ပါသည်။

ဦးစွာ၊ နမူနာဖြန့်ချီခြင်းဆိုသည်မှာ မည်သည်ကို သတ်မှတ်ခြင်းဖြင့် စတင်ကြပါစို့။ နမူနာဖြန့်ဝေခြင်း ဆိုသည်မှာ ကိန်းဂဏန်းစာရင်းအင်းလူဦးရေမှ ဖြစ်နိုင်သောနမူနာအားလုံးကို ထည့်သွင်းတွက်ချက်ခြင်းမှ ထွက်ပေါ်လာသော ဖြန့်ဝေမှုဖြစ်သည်။

ထို့ကြောင့်၊ အချိုးအစားနမူနာဖြန့်ဝေခြင်းသည် လူဦးရေတစ်ခုစီမှ ဖြစ်နိုင်သည့်နမူနာတစ်ခုစီ၏ အချိုးအစားကို တွက်ချက်ခြင်းမှ ထွက်ပေါ်လာသော ဖြန့်ဖြူးခြင်းဖြစ်သည်။ ဆိုလိုသည်မှာ၊ ကျွန်ုပ်တို့သည် လူဦးရေတစ်ခုမှဖြစ်နိုင်သောနမူနာအားလုံးကို လေ့လာပြီး နမူနာတစ်ခုစီ၏အချိုးအစားကို တွက်ချက်ပါက၊ တွက်ချက်ထားသောတန်ဖိုးများသည် နမူနာအချိုးအစားများကို နမူနာခွဲဝေမှုတစ်ခုဖြစ်သည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။