ပင်စည်နှင့် အရွက်ပုံ

ဤဆောင်းပါးတွင် စာရင်းဇယားများတွင် ပင်စည်နှင့် အရွက်ပုံများကို မည်သည့်အရာအတွက် အသုံးပြုကြောင်း ရှင်းပြထားသည်။ ထို့ကြောင့် ပင်စည်-အရွက်ပုံကြမ်းကို မည်သို့တည်ဆောက်ရမည်၊ ဤကိန်းဂဏန်းဂရပ်အမျိုးအစားအတွက် ဖြေရှင်းထားသော လေ့ကျင့်ခန်းများနှင့် နောက်ဆုံးတွင် ပင်စည်-ရွက်ပုံဇယား၏ အားသာချက်များနှင့် အားနည်းချက်များသည် အဘယ်နည်း။

ပင်စည်-အရွက် ပုံကြမ်းကား အဘယ်နည်း။

ပင်စည်နှင့် အရွက်ပုံမျဉ်း သည် ကိန်းဂဏန်းအချက်အလက်အစုအဝေးကို ကိုယ်စားပြုသည့် ကိန်းဂဏန်းဇယားအမျိုးအစားတစ်ခုဖြစ်သည်။

ပင်စည်-အရွက်ပုံကြမ်းတွင်၊ ဒေတာအမှတ်တစ်ခုစီကို ၎င်း၏နောက်ဆုံးဂဏန်းဖြစ်သည့် အရွက် နှင့် ကျန်ဂဏန်းများဖြစ်သည့် အရွက် ဖြင့် ပိုင်းခြားထားသည်။ ထို့ကြောင့်၊ ပင်စည်-အရွက်ပုံဇယားတွင် အရွက်တစ်ခုစီကို ၎င်း၏သက်ဆိုင်ရာပင်စည်၏မျဉ်းပေါ်တွင် ထားရှိသည်။

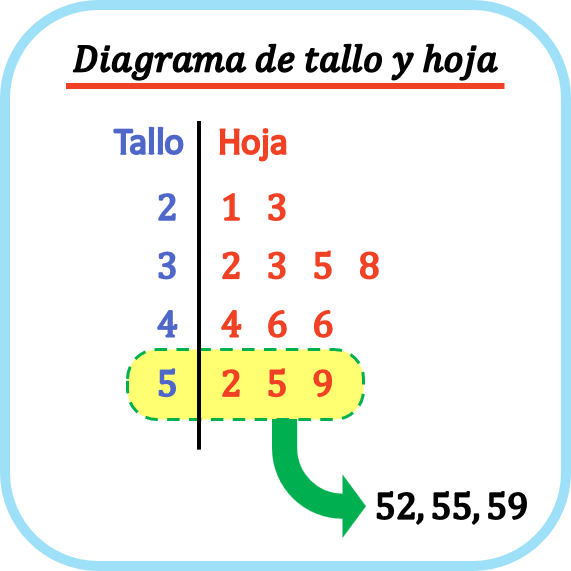
ဤနည်းအားဖြင့်၊ ပင်စည်နှင့် အရွက်ကွက်များသည် ကိန်းဂဏန်းအချက်အလက်အစုအဝေးကို ဂရပ်ဖစ်ပုံဖော်ရန် ကူညီပေးပြီး ဖြန့်ဖြူးမှု၏ပုံသဏ္ဍာန်ကိုလည်း မြင်သာစေရန် ကူညီပေးပါသည်။

ပင်စည်နှင့် အရွက်ပုံမျဉ်းကို အင်္ဂလိပ်မှ ဆင်းသက်လာသော ပင်စည်နှင့် အရွက်ပုံမျဉ်း ဟုလည်း ခေါ်သည်။

ပင်စည်နှင့် အရွက်ပုံဆွဲခြင်းသည် ဟီစတိုဂရမ် နှင့် အလွန်ဆင်တူသော်လည်း ဤအခြားကိန်းဂဏန်းဂရပ်အမျိုးအစားကို ပိုကြီးသောနမူနာအရွယ်အစားများအတွက် အသုံးပြုပါသည်။

ပင်စည်နှင့် အရွက်ပုံကြမ်းပြုလုပ်နည်း

ပင်စည်နှင့် အရွက်ပုံကြမ်းကို ဖန်တီးရန်၊ ဤအဆင့်များကို လိုက်နာပါ-

1. ဒေတာကို အသေးဆုံးမှ အကြီးဆုံးသို့ စီပါ။
2. လိုအပ်ပါက ဂဏန်းများကို လိုချင်သော ဂဏန်းများ ရသည်အထိ လှည့်ပါ။
3. ပင်စည်နှင့် အရွက်ကြားတွင် မည်သည့်ပုံသဏ္ဍန်ကို ဖြတ်ရမည်ကို ဆုံးဖြတ်ပါ၊ ဆိုလိုသည်မှာ အရွက်ရှိမည့် ကိန်းဂဏန်း အရေအတွက်ကို ဆုံးဖြတ်ပါ။ ပုံမှန်အားဖြင့်၊ စာရွက်သည် ဒေတာတစ်ခုစီ၏ နောက်ဆုံးဂဏန်းများသာ ပါဝင်ရန် ဒီဇိုင်းထုတ်ထားသည်။
4. ပင်မ နှင့် အရွက် ပုံကြမ်းတွင် ဒေတာအပိုင်းတစ်ခုစီကို ကိုယ်စားပြုသည်။ ပင်စည်များကို ဘယ်ကော်လံတွင် ငယ်စဉ်ကြီးလိုက် ထားရှိရပြီး အရွက်များကို သက်ဆိုင်ရာ ပင်စည်၏ အမြင့်တွင် အကြီးလိုက် ညာဘက်ကော်လံတွင် ထားရှိထားပါသည်။

Stem and Leaf Plot ၏ ဥပမာ

ထို့ကြောင့် ပင်စည်နှင့် အရွက်ပုံကြမ်းကို ဖန်တီးနည်းကို သင်တွေ့မြင်နိုင်သည်၊ အောက်ဖော်ပြပါ ဥပမာနှစ်ခုကို ကျွန်ုပ်တို့ဖြေရှင်းသည်- တစ်ခုသည် ဒဿမများမပါသော၊ နောက်တစ်ခုသည် ဒဿမများဖြစ်သည်။

ဥပမာ ၁

• ပင်စည် နှင့် အရွက် ပုံကြမ်းတွင် အောက်ပါ ဒေတာစီးရီးကို ပုံဖော်ပါ ။

ဤအခြေအနေမျိုးတွင် ဒေတာကို စီထားကာ ပတ်ထားပြီးဖြစ်သောကြောင့် ဤအဆင့်နှစ်ဆင့်ကို လုပ်ဆောင်ရန် မလိုအပ်ပါ။ ထို့ကြောင့်၊ ဂဏန်းများသည် ဂဏန်းနှစ်လုံးရှိသောကြောင့်၊ ၎င်းတို့သည် tenses များသည် ပင်မ၊

ပထမဦးစွာ ပုံ၏ ပင်စည်ကို ကိုယ်စားပြုပါမည်။ ဒေတာ၏ tense သည် 9 အထိတက်သည်၊ ထို့ကြောင့် ဆယ်ခုစီအတွက် စာကြောင်းတစ်ခုလုပ်သည်-

ပြီးလျှင် အရွက်များကို ကိုယ်စားပြုသည်၊ ဤအတွက်၊ ကျွန်ုပ်တို့သည် ဒေတာတစ်ခုစီ၏ ယူနစ်ကို ၎င်း၏သက်ဆိုင်ရာမျဉ်းတွင် ထားရှိသည်။ ဥပမာအားဖြင့်၊ နံပါတ် 57 သည် root 5 သို့သွားမည်ဖြစ်ပြီး ညာဘက်ကော်လံတွင် 7 ကိုထည့်ပါမည်။

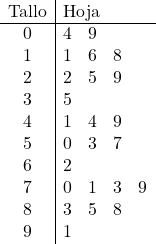
ဤနည်းအားဖြင့် နမူနာဒေတာအားလုံးကို ပင်စည်နှင့် အရွက်ကွက်ကွက်တစ်ခုတွင် ကိုယ်စားပြုခဲ့သည်။

ဥပမာ ၂

• အောက်ဖော်ပြပါ ဒေတာနမူနာနှစ်ခုကို ပင်စည်နှင့် အရွက်ကွက်ကွက်ကို အသုံးပြု၍ ဒဿမများနှင့် နှိုင်းယှဉ်ပါ။

ဤလေ့ကျင့်ခန်းတွင် သင်တွေ့မြင်ရမည့်အတိုင်း၊ ကိန်းဂဏန်းနမူနာနှစ်ခုကို ကိုယ်စားပြုရန်အတွက် ပင်စည်နှင့် အရွက်ကွက်ကွက်တစ်ခုကို အသုံးပြုနိုင်သည်။ ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် တူညီသော ပင်စည်နှင့် အရွက်ကွက်တွင် ဒေတာအတွဲနှစ်ခုလုံးကို ကွက်ကွက်ပါလိမ့်မည်- ဘယ်ဘက်တွင် တစ်ခုနှင့် ညာဘက်တွင် တစ်ခု။ ဤကွက်အမျိုးအစားကို နှစ်ထပ်ပင်စည်နှင့် အရွက်ကွက် ဟု ခေါ်သည်။

ဤကိစ္စတွင်၊ ကျွန်ုပ်တို့သည် ကိန်းဂဏာန်း၏ ပင်စည်အဖြစ် ကိန်းဂဏာန်းတစ်ခုလုံးကို ယူမည်ဖြစ်ပြီး၊ အခြားတစ်ဖက်တွင်၊ ဒဿမများသည် ပုံကြမ်း၏ အရွက်များဖြစ်လိမ့်မည်။ ထို့ကြောင့် ပင်စည်နှင့် အရွက်ပုံစံကို အစိတ်အပိုင်းအားလုံးကို နေရာချထားခြင်းဖြင့် တည်ဆောက်သည်။

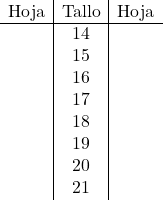
ယခု ကျွန်ုပ်တို့သည် ၎င်းနှင့်ကိုက်ညီသော အချက်အလက်တစ်ခုစီ၏ စာရွက်ကို ပင်မတွင် ထားလိုက်သည်-

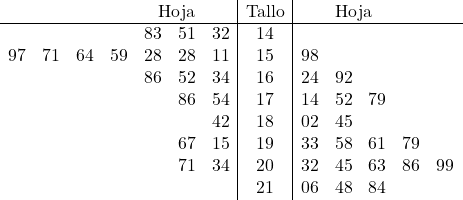
ဒေတာကို ဂရပ်ဖစ်ဖြင့် ကိုယ်စားပြုခြင်းဖြင့်၊ ၎င်းကို ကျွန်ုပ်တို့ အလွယ်တကူ နှိုင်းယှဉ်နိုင်သည်။ အတိအကျအားဖြင့်၊ ညာဘက်ရှိနမူနာဒေတာသည် ဘယ်ဘက်ရှိနမူနာထက် အနည်းငယ်ပိုကြီးသည်ကို ကျွန်ုပ်တို့မြင်ရသောကြောင့် ၎င်း၏ပျမ်းမျှသည်လည်း ပိုကြီးမည်ဖြစ်သည်။ ထို့ကြောင့် စာရင်းအင်းလေ့လာမှု၏ ရည်ရွယ်ချက်ပေါ် မူတည်၍ ကျွန်ုပ်တို့သည် ဤ သို့မဟုတ် ထိုနမူနာကို ရွေးချယ်ရန် စိတ်ဝင်စားမည်ဖြစ်သည်။

မျဥ်းစောင်းနှင့် ဘလိတ်ဇယားကို မည်သို့တည်ဆောက်ရမည်ကို သိရုံသာမက ဇယားကို အနက်ပြန်ဆိုပုံကိုလည်း သိရန် လိုအပ်ကြောင်း သတိရပါ။

ပင်မနှင့် အရွက်၏ အားသာချက်များနှင့် အားနည်းချက်များ

ပင်စည်နှင့် အရွက်ပုံသဏ္ဍာန်များကြောင့် အဆိုပါမြေကွက်အမျိုးအစားများသည် အောက်ပါ အားသာချက်များနှင့် အားနည်းချက်များရှိသည်။

အားသာချက်-

• ပင်စည်နှင့် အရွက်များကို ခြေရာခံခြင်းဖြင့် ဖြန့်ဖြူးပုံသဏ္ဍာန်ကို မြင်တွေ့နိုင်မည်ဖြစ်သည်။
• နှစ်ထပ်ပင်စည်နှင့် အရွက်ကွက်ကို အသုံးပြု၍ ဖြန့်ဖြူးမှုနှစ်ခုကို နှိုင်းယှဉ်နိုင်သည်။
• ၎င်းသည် သင့်အား ဒေတာအတွဲတစ်ခုတွင် အစွန်းအထင်းများကို အမြန်ဖော်ထုတ်နိုင်စေပါသည်။
• ဒေတာစီးရီး၏မုဒ်ကို မျက်လုံးဖြင့် သင်ဆုံးဖြတ်နိုင်သည်။

အားနည်းချက်များ-

• ကွန်ပြူတာဆော့ဖ်ဝဲလ်သည် ပိုမိုရှုပ်ထွေးသောဂရပ်တစ်ခုကို လျင်မြန်စွာဖန်တီးနိုင်သောကြောင့် ပင်စည်နှင့်အရွက်ပုံကြမ်းကို အသုံးပြုမှု လျော့နည်းလာပါသည်။
• ကိုယ်စားပြုရန် နမူနာအရွယ်အစားကို ယေဘုယျအားဖြင့် ဒေတာအချက် ၁၅ နှင့် ၁၅၀ ကြားတွင် ကန့်သတ်ထားသည်။
• ကိန်းဂဏန်း အချက်အလက်များကိုသာ ကိုယ်စားပြုနိုင်သည်။