Stata တွင် ပုံမှန်အခြေအနေအတွက် စမ်းသပ်နည်း

ကိန်းဂဏန်းစမ်းသပ်မှုများစွာသည် စမ်းသပ်မှုရလဒ်များကို ယုံကြည်စိတ်ချရရန်အတွက် ပုံမှန်အားဖြင့် ကိန်းရှင်တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော ကိန်းရှင်များကို ဖြန့်ဝေ ရန် လိုအပ်သည်။

ဤသင်ခန်းစာသည် Stata ရှိ variable များကြား ပုံမှန်ဖြစ်နိုင်ခြေအတွက် စမ်းသပ်ရန် သင်အသုံးပြုနိုင်သည့် နည်းလမ်းများစွာကို ရှင်းပြထားသည်။

ဤနည်းလမ်းတစ်ခုစီအတွက်၊ ကျွန်ုပ်တို့သည် auto ဟုခေါ်သော built-in Stata dataset ကို အသုံးပြုပါမည်။ အောက်ပါ command ကို အသုံးပြု၍ ဤဒေတာအတွဲကို သင်တင်နိုင်သည်-

အလိုအလျောက်စနစ်အသုံးပြုခြင်း။

နည်းလမ်း 1- ဟစ်စတိုဂရမ်များ

ကိန်းရှင်တစ်ခုအား ပုံမှန်ဖြန့်ဝေခြင်း ရှိ၊ မရှိ သိရန် အလွတ်သဘောနည်းလမ်းမှာ variable ၏ဖြန့်ဝေမှုကိုပြသရန် histogram တစ်ခုဖန်တီးရန်ဖြစ်သည်။

ကိန်းရှင် ကို ပုံမှန်အတိုင်း ဖြန့်ဝေပါက၊ အလယ်ဗဟိုအနီးတွင်ရှိသော တန်ဖိုးများနှင့် အမြီးပေါ်ရှိ တန်ဖိုးအနည်းငယ်သာရှိသော တန်ဘိုးပိုရှိသော “ ခေါင်းလောင်း” ပုံသဏ္ဍာန်ကို ဟီစတိုဂရမ်က ယူသင့်သည်။

variable displacement အတွက် histogram တစ်ခုဖန်တီးရန် hist command ကိုသုံးနိုင်သည်။

ရွေ့လျားမှုသမိုင်း

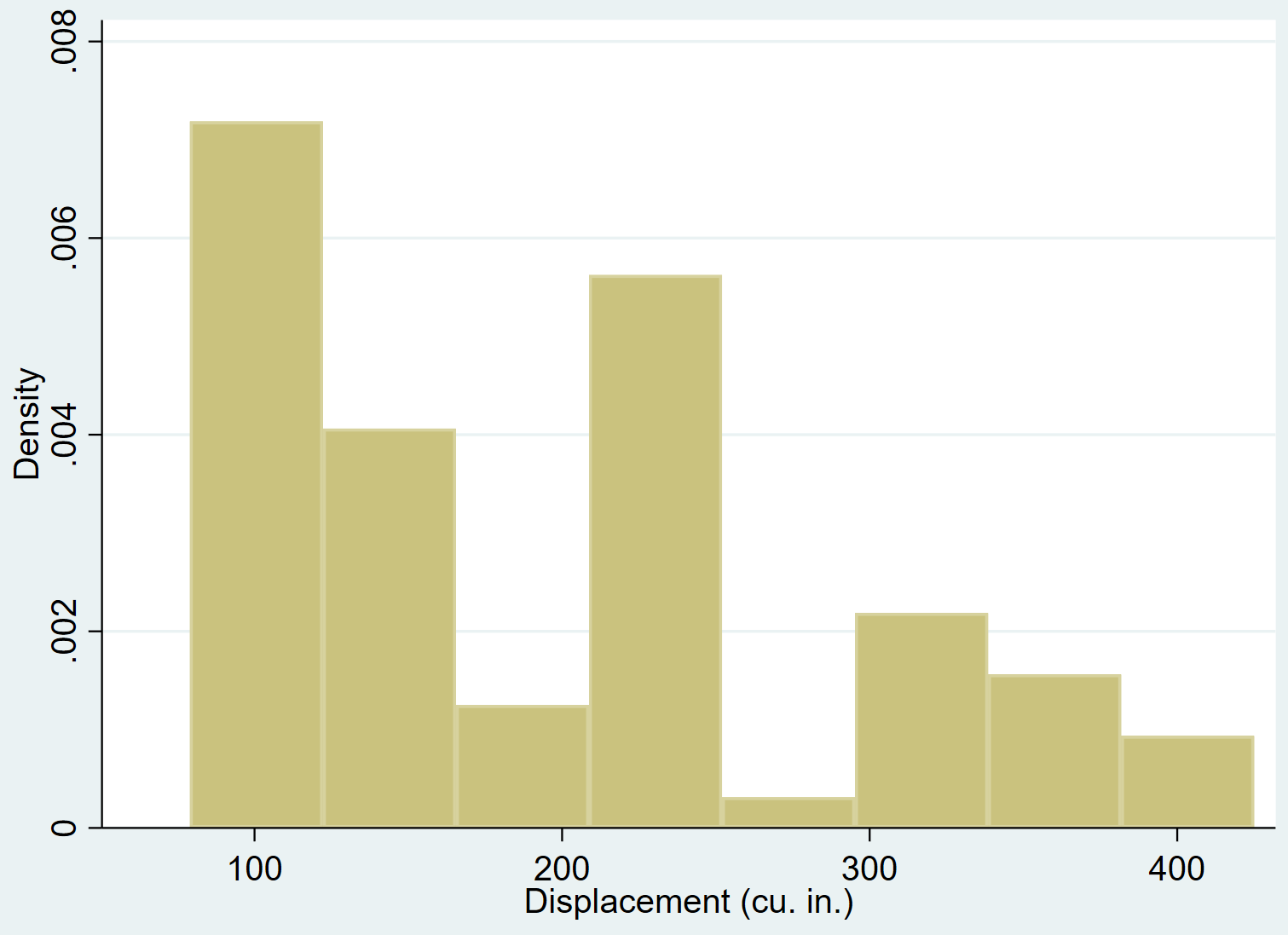
သာမာန် အမိန့်ကို အသုံးပြု၍ ပုံမှန် သိပ်သည်းဆမျဉ်းကွေးကို ဟီစတိုဂရမ်တစ်ခုသို့ ထည့်နိုင်သည်။

ရွေ့လျားမှုသမိုင်း၊ ပုံမှန်

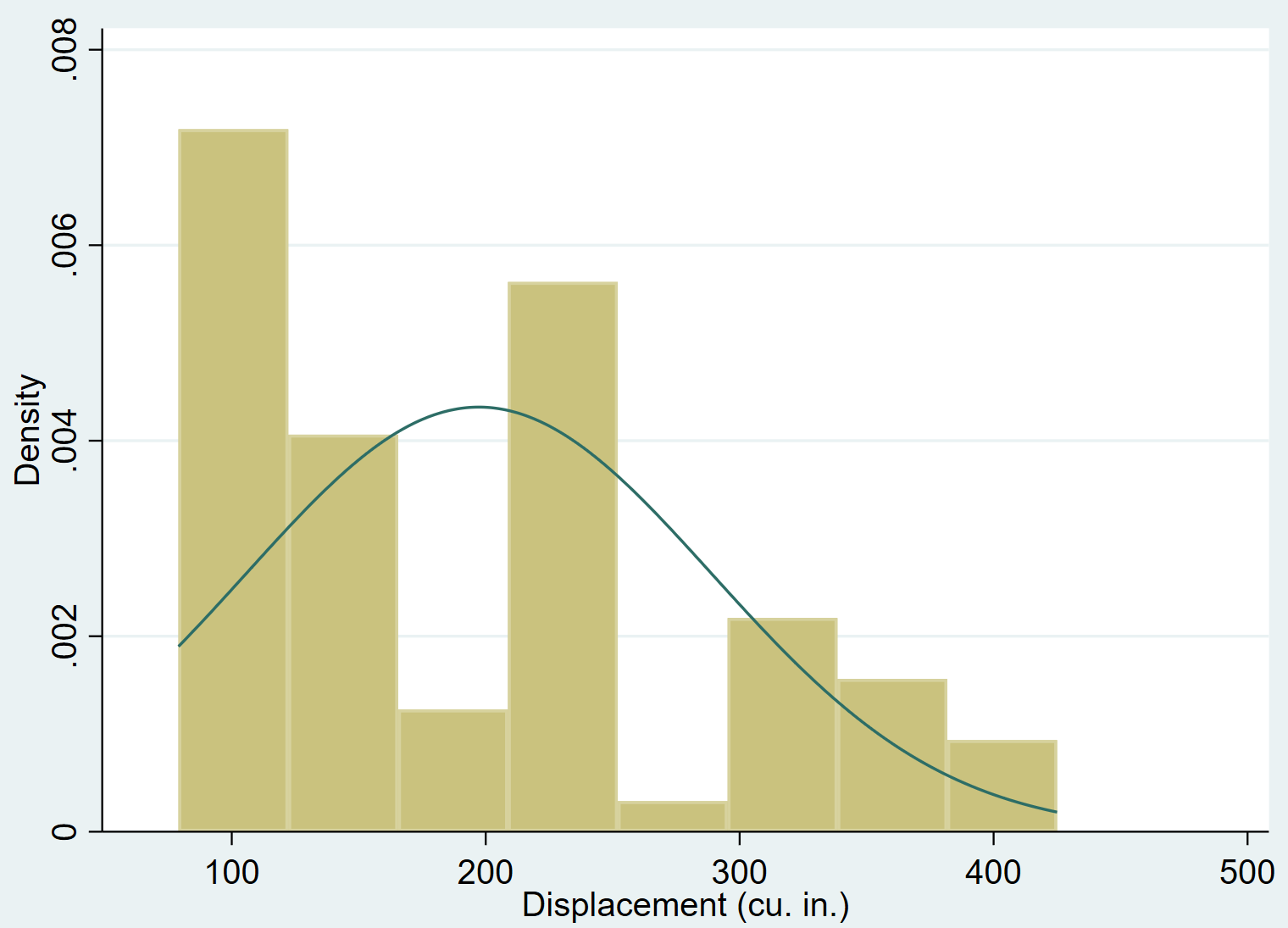
ကိန်းရှင် ပြောင်းလဲမှု သည် ညာဘက်သို့ စောင်းသွားကြောင်း သိသာထင်ရှားလှသည် (ဥပမာ တန်ဖိုးအများစုသည် ဘယ်ဘက်တွင် စုစည်းနေပြီး တန်ဖိုးများ၏ ညာဘက်သို့ ရှည်လျားသော “ အမြီး” သည်) သာမာန်ဖြန့်ဖြူးမှုကို မလိုက်နာကြောင်း သိသာထင်ရှားပါသည်။

ဆက်စပ်- ဘယ်နှင့်ညာ ကွဲလွဲသော ဖြန့်ဝေမှုများ

နည်းလမ်း 2: Shapiro-Wilk စမ်းသပ်မှု

ပုံမှန်အခြေအနေအတွက် စမ်းသပ်ရန် တရားဝင်နည်းလမ်းမှာ Shapiro-Wilk စမ်းသပ်မှုကို အသုံးပြုခြင်းဖြစ်သည်။

ဤစမ်းသပ်မှုအတွက် null hypothesis မှာ variable ကို ပုံမှန်အတိုင်း ဖြန့်ဝေနေခြင်းဖြစ်သည်။ အကယ်၍ စမ်းသပ်မှု၏ p-value သည် အချို့သော အရေးပါမှုအဆင့်အောက်တွင် ရှိနေပါက (ဘုံရွေးချယ်မှုများတွင် 0.01၊ 0.05၊ နှင့် 0.10) သည် null hypothesis ကို ငြင်းပယ်နိုင်ပြီး variable ကို ပုံမှန်ဖြန့်ဝေခြင်းမဟုတ်ကြောင်း အခိုင်အမာသက်သေပြရန် လုံလောက်သော အထောက်အထားရှိကြောင်း ကောက်ချက်ချနိုင်ပါသည်။ .

* စူးစမ်းမှုစုစုပေါင်း 4 နှင့် 2,000 ကြားရှိသောအခါ ဤစမ်းသပ်မှုကို အသုံးပြုနိုင်သည်။

ပြောင်းလဲနိုင်သော နေရာရွှေ့ပြောင်းမှုတွင် Shapiro-Wilk စမ်းသပ်မှုကို လုပ်ဆောင်ရန် swilk အမိန့်ကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်သည်။

ချောမွေ့လှုပ်ရှားမှု

ဤတွင် စမ်းသပ်မှုရလဒ်ကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်သည်-

Obs- 74။ ဤသည်မှာ စမ်းသပ်မှုတွင် အသုံးပြုသည့် လေ့လာတွေ့ရှိချက် အရေအတွက်ဖြစ်သည်။

W: 0.92542။ ဤသည်မှာ စာမေးပွဲအတွက် ကိန်းဂဏန်းများဖြစ်သည်။

Prob>z- 0.00031။ ၎င်းသည် စမ်းသပ်စာရင်းအင်းနှင့် ဆက်စပ်နေသည့် p-တန်ဖိုးဖြစ်သည်။

p-value သည် 0.05 ထက်နည်းသောကြောင့်၊ test ၏ null hypothesis ကို ငြင်းပယ်နိုင်ပါသည်။ ပြောင်းလဲနိုင်သော ရွှေ့ပြောင်းခြင်းကို ပုံမှန်အတိုင်း ဖြန့်ဝေခြင်းမဟုတ်ကြောင်း ပြောရန် ကျွန်ုပ်တို့တွင် လုံလောက်သော အထောက်အထားရှိသည်။

swilk command ပြီးနောက် များစွာသော variable များကို စာရင်းပြုစုခြင်းဖြင့် ကျွန်ုပ်တို့သည် Shapiro-Wilk test ကို တစ်ကြိမ်တည်းတွင် variable အများအပြားတွင် လုပ်ဆောင်နိုင်သည်-

swilk displacement စိုင်းစိုင်းခမ်းလှိုင် အရှည်

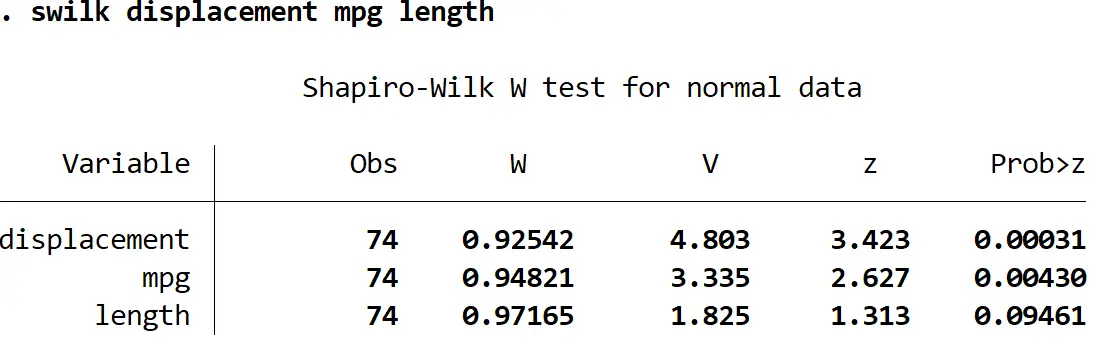
0.05 ၏ အရေးပါမှုအဆင့်ကို အသုံးပြု၍ ရွှေ့ပြောင်းခြင်း နှင့် စိုင်းစိုင်းခမ်းလှိုင်ကို ပုံမှန်ဖြန့်ဝေခြင်းမဟုတ်ကြောင်း ကောက်ချက်ချနိုင်သော်လည်း အရှည်အား ပုံမှန်ဖြန့်ဝေခြင်းမရှိဟု ကျွန်ုပ်တို့တွင် လုံလောက်သောအထောက်အထားမရှိပါ။

နည်းလမ်း 3- Shapiro-Francia စမ်းသပ်မှု

ပုံမှန်အခြေအနေအတွက် စမ်းသပ်ရန် နောက်ထပ်တရားဝင်နည်းလမ်းမှာ Shapiro-Francia စမ်းသပ်မှုကို အသုံးပြုခြင်းဖြစ်သည်။

ဤစမ်းသပ်မှုအတွက် null hypothesis မှာ variable ကို ပုံမှန်အတိုင်း ဖြန့်ဝေနေခြင်းဖြစ်သည်။ စမ်းသပ်မှု၏ p-value သည် အချို့သော အရေးပါမှုအဆင့်အောက်တွင် ရှိနေပါက၊ ထို့နောက် null hypothesis ကို ငြင်းပယ်နိုင်ပြီး ကိန်းရှင်သည် ပုံမှန်အတိုင်း ဖြန့်ဝေခြင်းမရှိကြောင်း လုံလောက်သော အထောက်အထားရှိသည်ဟု ကောက်ချက်ချနိုင်သည်။

* စူးစမ်းမှုစုစုပေါင်း 10 နှင့် 5,000 ကြားရှိသောအခါ ဤစမ်းသပ်မှုကို အသုံးပြုနိုင်သည်။

Shapiro-Wilk Test ကို variable displacement လုပ်ရန် sfrancia command ကိုသုံးနိုင်သည်။

ရွှေ့လျားစဖရန်စီယမ်

ဤတွင် စမ်းသပ်မှုရလဒ်ကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်သည်-

Obs- 74။ ဤသည်မှာ စမ်းသပ်မှုတွင် အသုံးပြုသည့် လေ့လာတွေ့ရှိချက် အရေအတွက်ဖြစ်သည်။

W’: 0.93011။ ဤသည်မှာ စာမေးပွဲအတွက် ကိန်းဂဏန်းများဖြစ်သည်။

Prob>z- 0.00094။ ၎င်းသည် စမ်းသပ်စာရင်းအင်းနှင့် ဆက်စပ်နေသည့် p-တန်ဖိုးဖြစ်သည်။

p-value သည် 0.05 ထက်နည်းသောကြောင့်၊ test ၏ null hypothesis ကို ငြင်းပယ်နိုင်ပါသည်။ ပြောင်းလဲနိုင်သော ရွှေ့ပြောင်းခြင်းကို ပုံမှန်အတိုင်း ဖြန့်ဝေခြင်းမဟုတ်ကြောင်း ပြောရန် ကျွန်ုပ်တို့တွင် လုံလောက်သော အထောက်အထားရှိသည်။

Shapiro-Wilk စမ်းသပ်မှုကဲ့သို့ပင်၊ သင်သည် sfrancia အမိန့်ပြီးနောက် ကိန်းရှင်အများအပြားကို စာရင်းပြုစုခြင်းဖြင့် Shapiro-Francia စမ်းသပ်မှုကို တစ်ကြိမ်တည်းလုပ်ဆောင်နိုင်သည်။

နည်းလမ်း 4- skewness နှင့် kurtosis စမ်းသပ်ခြင်း။

ပုံမှန်အခြေအနေအတွက် စမ်းသပ်ရန် အခြားနည်းလမ်းမှာ ကွဲပြားမှု၏ skewness နှင့် kurtosis သည် ပုံမှန်ဖြန့်ဖြူးမှုနှင့် ကိုက်ညီမှုရှိမရှိ ဆုံးဖြတ်ပေးသည့် skewness and kurtosis test ကို အသုံးပြုရန်ဖြစ်သည်။

ဤစမ်းသပ်မှုအတွက် null hypothesis မှာ variable ကို ပုံမှန်အတိုင်း ဖြန့်ဝေနေခြင်းဖြစ်သည်။ စမ်းသပ်မှု၏ p-value သည် အချို့သော အရေးပါမှုအဆင့်အောက်တွင် ရှိနေပါက၊ ထို့နောက် null hypothesis ကို ငြင်းပယ်နိုင်ပြီး ကိန်းရှင်သည် ပုံမှန်အတိုင်း ဖြန့်ဝေခြင်းမရှိကြောင်း လုံလောက်သော အထောက်အထားရှိသည်ဟု ကောက်ချက်ချနိုင်သည်။

*ဤစမ်းသပ်မှုကို အသုံးပြုရန် အနည်းဆုံး ၈ ချက် လိုအပ်သည်။

variable displacement တွင် skewness and kurtosis test ကိုလုပ်ဆောင်ရန် sktest command ကိုသုံးနိုင်သည်။

ရွေ့လျားစမ်းသပ်မှု

ဤသည်မှာ စမ်းသပ်မှုရလဒ်ကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်သည်-

Obs- 74။ ဤသည်မှာ စမ်းသပ်မှုတွင် အသုံးပြုသည့် လေ့လာတွေ့ရှိချက် အရေအတွက်ဖြစ်သည်။

adj chi(2): 5.81။ ဤသည်မှာ စမ်းသပ်မှုအတွက် Chi-square စမ်းသပ်မှု ကိန်းဂဏန်းဖြစ်သည်။

Prob>chi2: 0.0547။ ၎င်းသည် စမ်းသပ်စာရင်းအင်းနှင့် ဆက်စပ်နေသည့် p-တန်ဖိုးဖြစ်သည်။

p-value သည် 0.05 ထက်မနည်းသောကြောင့်၊ စမ်းသပ်မှု၏ null hypothesis ကို ငြင်းပယ်ရန် ပျက်ကွက်ပါသည်။ လှုပ်ရှားမှုများကို ပုံမှန်ဖြန့်ဝေခြင်းမရှိဟု ဆိုရန် လုံလောက်သော သက်သေမရှိပါ။

အခြားသော ပုံမှန်စစ်ဆေးမှုများနှင့် အလားတူ၊ သင်သည် sktest command ပြီးနောက် များစွာသော variable များကို စာရင်းပြုစုခြင်းဖြင့် ကိန်းရှင်များစွာကို တစ်ကြိမ်တည်းတွင် skewness နှင့် kurtosis စမ်းသပ်မှုကို လုပ်ဆောင်နိုင်သည်။