ပျမ်းမျှအမျိုးအစားများ (စာရင်းအင်းများ)

အားဖြင့် Benjamin Anderson ဩဂုတ် 6, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤတွင် ကျွန်ုပ်တို့သည် ကိန်းဂဏန်းစာရင်းဇယားများတွင် ပျမ်းမျှအမျိုးအစားအားလုံးနှင့် ၎င်းတို့ကို တွက်ချက်ပုံတို့ကို ရှင်းပြပါသည်။ စတော့အိတ်အမျိုးအစားတစ်ခုစီအတွက် ပုံသေနည်းနှင့် ဥပမာများကို သင်တွေ့လိမ့်မည်။

သို့သော် ပျမ်းမျှအမျိုးအစားများကို မမြင်မီ၊ ကိန်းဂဏန်းစာရင်းဇယားများတွင် ပျမ်းမျှအား မည်သည်ကို ယုတ္တိရှိရှိသိရပါမည်။ ထို့ကြောင့်၊ ဆက်မလုပ်မီ အောက်ပါလင့်ခ်ကို တိုင်ပင်ရန် အကြံပြုအပ်ပါသည်။

➤ ကြည့်ပါ- ပျမ်းမျှ (ကိန်းဂဏန်း) ကဘာလဲ။

စာရင်းအင်းဆိုင်ရာ ပျမ်းမျှအမျိုးအစားများကား အဘယ်နည်း။

စာရင်းဇယားများတွင်၊ ပျမ်းမျှအမျိုးအစားများမှာ-

ဂဏန်းသင်္ချာ ပျမ်းမျှ
ပျမ်းမျှအလေးချိန်
ဂျီဩမေတြီဆိုသည်မှာ
root ဆိုသည်မှာ စတုရန်းဖြစ်သည်။
harmonic အဓိပ္ပာယ်
ယေဘုယျအားဖြင့် ပျမ်းမျှ
ယေဘုယျအားဖြင့် f-ပျမ်းမျှ
ဖြတ်တောက်ခြင်းကို ဆိုလိုသည်။
interquartile ကို ဆိုလိုသည်။
လုပ်ဆောင်ချက်တစ်ခု၏ပျမ်းမျှ

ဆက်လက်၍ စာရင်းဇယားများတွင် ပျမ်းမျှအမျိုးအစားအားလုံးကို တွက်ချက်နည်းကို ရှင်းပြပါမည်။ အသုံးအများဆုံး ပျမ်းမျှအမျိုးအစားငါးမျိုးမှာ ဂဏန်းသင်္ချာပျမ်းမျှ၊ အလေးချိန်ပျမ်းမျှ၊ ဂျီဩမေတြီပျမ်းမျှ၊ လေးထောင့်ပုံပျမ်းမျှနှင့် ဟာမိုနစ်ပျမ်းမျှတို့ဖြစ်သည်။ ဒါကြောင့် ဒီအဓိက မီဒီယာ အမျိုးအစား ငါးမျိုးအကြောင်း အသေးစိတ်ကို တင်ပြပါမယ်။

ဂဏန်းသင်္ချာ ပျမ်းမျှ

ဂဏန်းသင်္ချာဆိုလို အား တန်ဖိုးများအားလုံးကို ပေါင်းထည့်ကာ ဒေတာအမှတ်စုစုပေါင်းဖြင့် ပိုင်းခြားခြင်းဖြင့် တွက်ချက်သည်။

ထို့ကြောင့် ဂဏန်းသင်္ချာပျမ်းမျှအတွက် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်။

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+\dots+x_N}{N}$

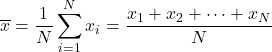
ဂဏန်းသင်္ချာဆိုလိုအား ဂဏန်းသင်္ချာ ဟုလည်း ခေါ်သည်။

ဂဏန်းသင်္ချာပျမ်းမျှသည် စာရင်းဇယားများတွင် အသုံးအများဆုံး ပျမ်းမျှအမျိုးအစားဖြစ်နိုင်သည်။

ဤပျမ်းမျှအမျိုးအစားကို မည်သို့ရယူသည်၏ နမူနာကိုကြည့်ရန်၊ အောက်ပါဒေတာများ၏ ဂဏန်းသင်္ချာပျမ်းမျှအား တွက်ချက်ပါမည်။

$4\quad 7\quad 10\quad 1\quad 8\quad9$

ဂဏန်းသင်္ချာ ပျမ်းမျှတွက်ရန်၊ ကိန်းဂဏန်းအချက်အလက်အားလုံးကို ပေါင်းထည့်ကာ စုစုပေါင်းဒေတာ အရေအတွက်အားဖြင့် 6 ဖြစ်သည်-

$\overline{x}=\cfrac{4+7+10+1+8+9}{6}=6,5$

ပျမ်းမျှအလေးချိန်

ကိုယ်အလေးချိန် ပျမ်းမျှကို တွက်ချက်ရန်၊ ကိန်းဂဏန်း အချက်အလက် တစ်ခုစီကို ၎င်း၏ အလေးချိန် (သို့မဟုတ်) အလေးချိန် ဖြင့် ဦးစွာ မြှောက်ပြီး ထုတ်ကုန် အားလုံးကို ပေါင်းထည့်ကာ နောက်ဆုံးတွင် အလေးချိန် ပေါင်းလဒ်ကို အလေးချိန် အားလုံး၏ ပေါင်းလဒ်ဖြင့် ပိုင်းခြားရပါမည်။

ထို့ကြောင့် အလေးချိန် ပျမ်းမျှဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်။

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+\dots x_N\cdot w_N}{w_1+w_2+\dosts +w_N}$

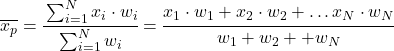
x _i သည် ကိန်းဂဏန်းတန်ဖိုးဖြစ်ပြီး w _{i သည်} ၎င်း၏သက်ဆိုင်ရာအလေးချိန်ဖြစ်သည်။

အလေးချိန် ပျမ်းမျှသည် နားလည်ရန် ပိုခက်ခဲသောကြောင့် ၎င်းကို တွက်ချက်ပုံအဆင့်ဆင့်ကို ရှင်းပြထားသည့် အောက်ပါဥပမာကို စစ်ဆေးကြည့်ရန် အကြံပြုလိုပါသည်-

➤ ကိုယ်အလေးချိန် ပျမ်းမျှ ဥပမာကို ကြည့်ပါ။

ဂျီဩမေတြီဆိုသည်မှာ

ကိန်းဂဏန်းအချက်အလက်အစုတစ်ခု၏ ဂျီဩမေတြီဆိုလိုသည်မှာ တန်ဖိုးအားလုံး၏ ထုတ်ကုန်၏ နံပါတ်မြောက်အမြစ်နှင့် ညီမျှသည်။

ဤပျမ်းမျှအမျိုးအစားကို လုပ်ငန်းဘဏ္ဍာရေးတွင် ပြန်အမ်းနှုန်းများ၊ ရာခိုင်နှုန်း ပျမ်းမျှများနှင့် ပေါင်းစပ်အတိုးများကို တွက်ချက်ရန် အသုံးပြုပါသည်။

ဤသိုလှောင်မှုအမျိုးအစားအတွက် ဖော်မြူလာမှာ အလွန်ရှုပ်ထွေးပါသည်။ အမှန်မှာ၊ ကိန်းဂဏန်း ကိန်းဂဏန်းများ အားလုံး၏ ဂျီဩမေတြီ ပျမ်းမျှအား တွက်ချက်၍ မရသော်လည်း တစ်ခါတစ်ရံ ဤဆိုလိုချက် အမျိုးအစားကို မဆုံးဖြတ်နိုင်ပါ။ ထို့ကြောင့် အောက်ပါလင့်ခ်တွင် ဖော်ပြထားသည့် ခြွင်းချက်အားလုံးကို တိုင်ပင်ဆွေးနွေးရန် ကျွန်ုပ်တို့ အကြံပြုအပ်ပါသည်။

➤ ဂျီဩမေတြီ ပျမ်းမျှဖော်မြူလာကို ကြည့်ပါ။

root ဆိုသည်မှာ စတုရန်းဖြစ်သည်။

အရင်းဆိုလို နှစ်ထပ် သည် ဒေတာ၏ နှစ်ထပ်ကိန်းဂဏန်းသင်္ချာပျမ်းမျှ၏ နှစ်ထပ်ကိန်းနှင့် ညီမျှသည်။

ထို့ကြောင့် ပျမ်းမျှစတုရန်းပုံသေနည်းသည် အောက်ပါအတိုင်းဖြစ်သည်။

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

ဤပျမ်းမျှအမျိုးအစားကို root mean square ၊ root mean square သို့မဟုတ် RMS ဟုလည်းခေါ်သည်။

ကုဗပျှမ်းမျှလည်း ရှိနေကြောင်း ထောက်ပြကြပါစို့၊ သို့သော် အထူးကိစ္စများတွင် အသုံးပြုပါသည်။

စတုရန်းပျှမ်းမျှတွင် အားသာချက်များနှင့် အားနည်းချက်များ ရှိသည်၊ ဥပမာ၊ ကိန်းဂဏန်းကိန်းရှင်သည် အပြုသဘောနှင့် အနုတ်တန်ဖိုးများကို ယူသောအခါတွင် အထူးအသုံးဝင်သည်၊ အကြောင်းမှာ ဒေတာအပိုင်းအစတစ်ခုစီကို squaring လုပ်ခြင်းဖြင့် တန်ဖိုးများအားလုံးသည် အပြုသဘောဖြစ်လာသည်။ အောက်ပါလင့်ခ်ကိုနှိပ်ခြင်းဖြင့် ဤမီဒီယာအမျိုးအစား၏ နောက်ထပ်အင်္ဂါရပ်များကို သင်ကြည့်ရှုနိုင်သည်-

➤- root mean square ၏ အားသာချက်များနှင့် အားနည်းချက်များကို ကြည့်ပါ။

harmonic အဓိပ္ပါယ်

ဟာမိုနီဆိုလိုရင်းကို တန်ဖိုးတစ်ခုစီ၏ အပြန်အလှန်အကျိုးသက်ရောက်မှုများ၏ပေါင်းလဒ်ဖြင့် ကိန်းဂဏန်းအချက်အလက်စုစုပေါင်းအရေအတွက်ကို ပိုင်းခြားခြင်းဖြင့် တွက်ချက်သည်။

$\displaystyle H=\frac{N}{\displaystyle\sum_{i=1}^N\frac{1}{x_i}}=\frac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_N}}$

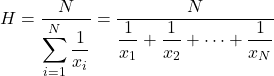
ပျမ်းမျှအမြန်နှုန်း၊ အချိန်များကို တွက်ချက်ရန် သို့မဟုတ် အီလက်ထရွန်နစ် တွက်ချက်မှုပြုလုပ်ရန် ဟာမိုနီပျမ်းမျှအား အသုံးပြုသည်။ ဤဝိသေသလက္ခဏာသည် စျေးနှုန်းပျမ်းမျှ သို့မဟုတ် ရာခိုင်နှုန်းများကို တွက်ချက်ရာတွင် မကြာခဏအသုံးပြုလေ့ရှိသည့် အခြားပျမ်းမျှအမျိုးအစားများနှင့် ဟာမိုနီပျမ်းမျှအား ကွဲပြားစေသည်။

အောက်ပါစာမျက်နှာတွင် ဤပျမ်းမျှအမျိုးအစားကို တွက်ချက်ခြင်း၏ ဥပမာများကို သင်ကြည့်ရှုနိုင်သည်-

➤- ဟာ မိုနစ် အဓိပ္ပာယ် နမူနာများကို ကြည့်ပါ။

အခြားခြေအိတ်အမျိုးအစားများ

ဤအပိုင်းတွင် အခြားခြေအိတ်အမျိုးအစားများအတွက် ဖော်မြူလာများကို ကျွန်ုပ်တို့တွေ့ရပါမည်။ အမျိုးအစားတစ်ခုစီကို တွင်တွင်ကျယ်ကျယ်အသုံးပြုခြင်းမရှိသောကြောင့် အမျိုးအစားတစ်ခုစီ၏အသေးစိတ်အချက်အလက်များကိုကျွန်ုပ်တို့မဖော်ပြသော်လည်း၊ အခြားခြေအိတ်အမျိုးအစားများရှိကြောင်းသိရန်သင့်အတွက်ကောင်းပါသည်။

ယေဘူယျအားဖြင့် ပျမ်းမျှ သည် အထက်ဖော်ပြပါ ပျမ်းမျှအမျိုးအစားများ၏ ရောနှောမှုဖြစ်ပြီး အောက်ပါဖော်မြူလာကို အသုံးပြု၍ တွက်ချက်သည်-

$\displaystyle\overline{x}(m) = \left ( \frac{1}{N}\cdot\sum_{i=1}^N{x_i^m} \right ) ^{1/m}$

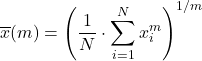
f သည် ထိုးသွင်း နှင့် မိုနိုတိုနစ် လုပ်ဆောင်ချက် ဖြစ်ပါစေ၊ ထို့နောက် ယေဘုယျအားဖြင့် သတ်မှတ်ထားသော f-mean သည်-

$\displaystyle\overline{x} = f^{-1}\left({\frac{1}{N}\cdot\sum_{i=1}^N{f(x_i)}}\right)$

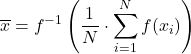
ဖြတ်တောက်ထားသော ဆိုလိုသည်မှာ နမူနာ၏ အထက်နှင့် အောက်စွန်းရှိ စူးစမ်းမှု ရာခိုင်နှုန်းတစ်ခုကို နုတ်ပြီးနောက် ဂဏန်းသင်္ချာပျမ်းမျှကို တွက်ချက်ခြင်းတွင် ပါဝင်ပါသည်။ တူညီသော ရာခိုင်နှုန်းကို နှစ်ဖက်စလုံးတွင် ပယ်ချသင့်သည်။

interquartile mean ကို တွက်ချက်ရန်အတွက် interquartile mean ဟုခေါ်သော ပထမနှင့် စတုတ္ထ quartiles မှ data များကို ပထမဦးစွာ စွန့်ပစ်ပြီး၊ ထို့နောက် နမူနာ၏ ဒုတိယနှင့် တတိယ quartiles တို့၏ ဂဏန်းသင်္ချာပျမ်းမျှကို တွက်ချက်ပါသည်။ ထို့ကြောင့် ဤပျမ်းမျှအမျိုးအစားအတွက် ဖော်မြူလာမှာ-

$\displaystyle\overline{x}={2 \over n} \sum_{i=\frac{n}{4}+1}^{\frac{3n}{4}}{x_i}$

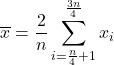
နောက်ဆုံးအနေနဲ့၊ function တစ်ခုရဲ့ ဆိုလိုရင်းကို သင်ရှာတွေ့နိုင်ပါတယ်။ ပိတ်ထားသောကြားကာလ [a,b] ရှိ စဉ်ဆက်မပြတ်လုပ်ဆောင်မှုတစ်ခု၏ ပျမ်းမျှတန်ဖိုးကို အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်သည်-

$\displaystyle\overline{f}=\frac{1}{b-a} \int_a^b f(t) dt$

နမူနာနှင့် လူဦးရေ ပျမ်းမျှ

နောက်ဆုံးတွင်၊ နမူနာ ပျမ်းမျှနှင့် လူဦးရေ ပျမ်းမျှအကြား ကွာခြားချက်၊ မကြာခဏ ရှုပ်ထွေးလေ့ရှိသော ပျမ်းမျှ အမျိုးအစား နှစ်မျိုးကို ကြည့်ပါမည်။

နမူနာဆိုလိုသည်မှာ ကိန်းရှင်နမူနာတစ်ခု၏ တန်ဖိုးများထက် ပျမ်းမျှတွက်ချက်မှုဖြစ်ပြီး ၎င်းသည် ကိန်းရှင်တစ်ခု၏ တန်ဖိုးအားလုံး၏ တစ်စိတ်တစ်ပိုင်းကို တွက်ချက်သည်ဟု ဆိုလိုသည်။

လူဦးရေ ပျမ်းမျှ ဆိုသည်မှာ စာရင်းအင်း လူဦးရေထက် တွက်ချက်ထားသော ပျှမ်းမျှဖြစ်ပြီး၊ ဆိုလိုသည်မှာ ကိန်းရှင်တစ်ခု၏ တန်ဖိုးများအားလုံးကို ကျော်သည်ဟု ဆိုနိုင်သည်။ ထို့ကြောင့် လူဦးရေဆိုသည်မှာ ကိန်းရှင်၏ သင်္ချာမျှော်မှန်းချက်နှင့် တိုက်ဆိုင်နေသည်။

လုံလောက်သောဒေတာပမာဏကိုသိပါက နမူနာဆိုလိုသည်မှာ လူဦးရေဆိုလိုသည်နှင့် တူညီသည်ဟု ယူဆနိုင်သည်။ သို့သော် လူဦးရေ၏တန်ဖိုးဆိုသည်မှာ ရရှိနိုင်ရန် အလွန်ခက်ခဲသောကြောင့် လက်တွေ့တွင် ဖြန့်ဖြူးမှုတစ်ခု၏တန်ဖိုးအားလုံးကို သိခဲပါသည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။