Kurtosis အနုတ်လက္ခဏာဖြစ်နိုင်ပါသလား။
စာရင်းဇယားများတွင်၊ ဖြစ်နိုင်ခြေဖြန့်ဝေမှုပုံစံကိုဖော်ပြရန် kurtosis ကိုအသုံးပြုသည်။
အတိအကျအားဖြင့်၊ ၎င်းသည် အမြီးများအတွင်း သို့မဟုတ် ဖြန့်ဖြူးမှုတစ်ခု၏ထိပ်တွင် ဒေတာတန်ဖိုးများ အစုအဝေးတွင် မည်မျှကောင်းမွန်ကြောင်း ကျွန်ုပ်တို့ကိုပြောပြသည်။
ဖြန့်ဖြူးမှုတစ်ခု၏ kurtosis သည် အနုတ်လက္ခဏာ၊ သုည သို့မဟုတ် အပြုသဘော ဖြစ်နိုင်သည်။
သုည Kurtosis
ဖြန့်ဖြူးမှုတစ်ခုတွင် 0 kurtosis ရှိပါက၊ ၎င်းသည် အောက်ဖော်ပြပါ ခေါင်းလောင်းပုံသဏ္ဍာန်ရှိသော ပုံမှန်ဖြန့်ဝေမှုနှင့် ညီမျှသည်-
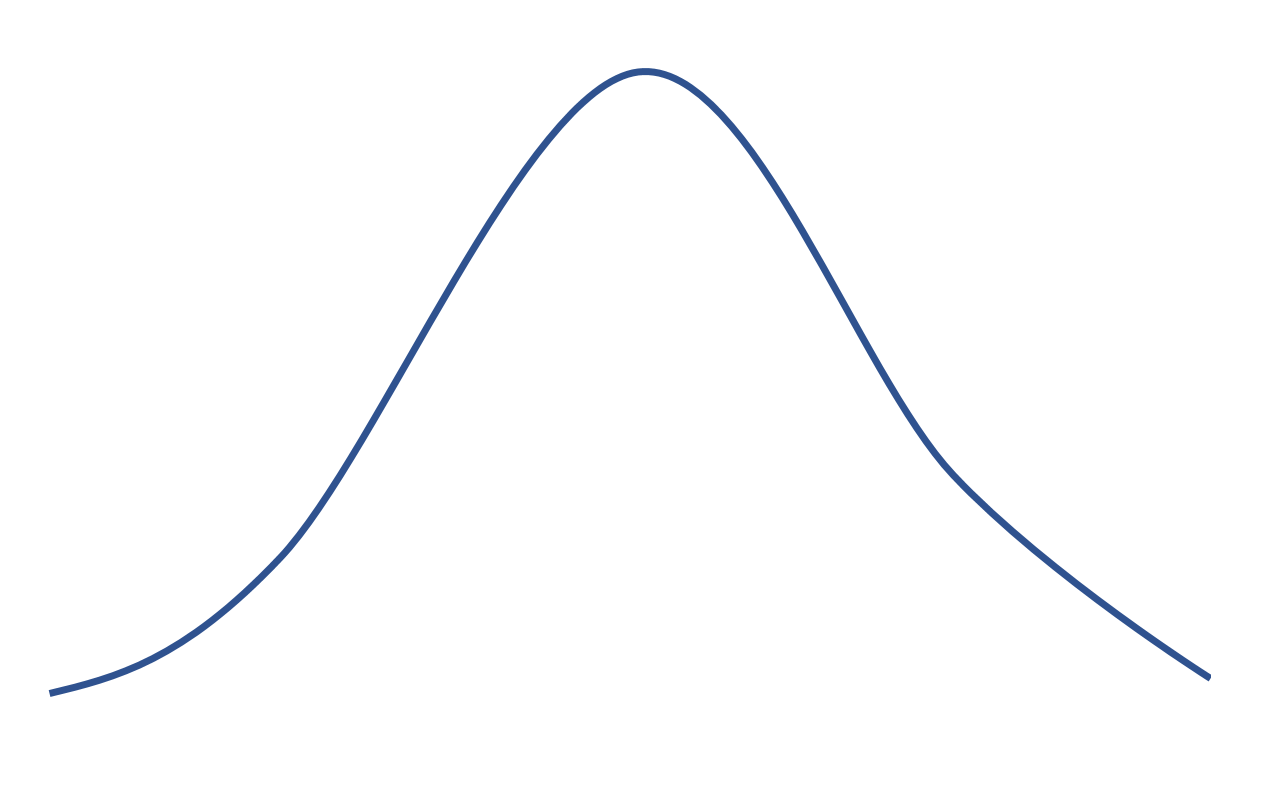
အပြုသဘော kurtosis
ဖြန့်ဖြူးမှုတစ်ခုတွင် positive kurtosis ရှိပါက၊ ၎င်းကို leptokurtic ဟုဆိုသည်၊ ဆိုလိုသည်မှာ ၎င်းသည် ပုံမှန်ဖြန့်ဖြူးမှုထက် ပိုမိုလေးလံသောအမြီးများရှိပြီး ၎င်းတွင် ပြတ်သားသောအမြီးများရှိသည်။
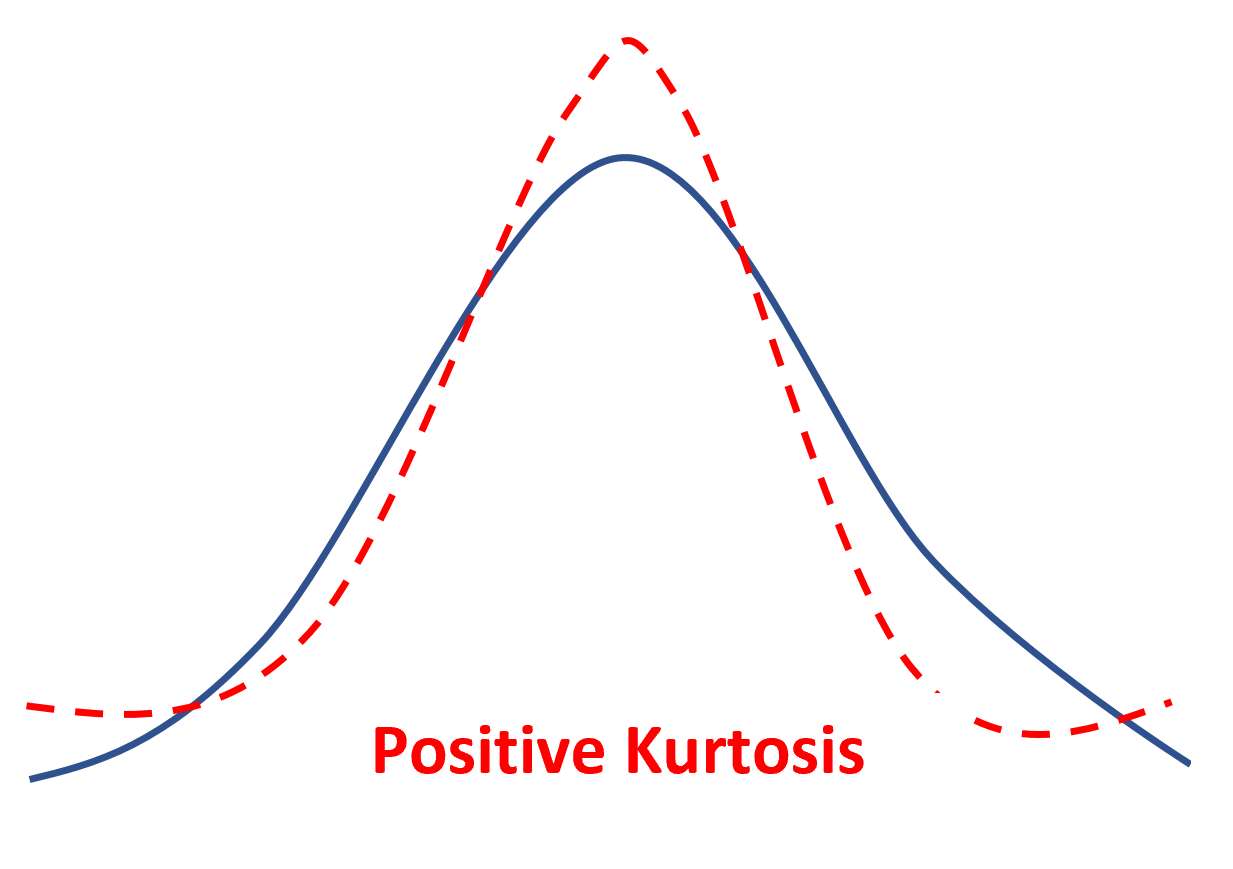
ရိုးရှင်းစွာဆိုလိုသည်မှာ ဒေတာတန်ဖိုးအနည်းငယ်သည် ဆိုလိုရင်းအနီးတွင် တည်ရှိပြီး ဒေတာတန်ဖိုးများ အမြီးပေါ်တွင် တည်ရှိနေပါသည်။
အပြုသဘောဆောင်သော kurtosis ပါ၀င်သော လူသိအများဆုံးဖြန့်ဝေမှုသည် သာမာန်ဖြန့်ဖြူးမှုထက် ပိုမိုပြတ်သားပြီး အမြီးများပိုမိုလေးလံသော t ဖြန့်ဖြူးခြင်းဖြစ်သည်။
အနုတ်လက္ခဏာ kurtosis
ဖြန့်ဖြူးမှုတစ်ခုတွင် negative kurtosis ရှိလျှင် ၎င်းကို platykurtic ဟုခေါ်သည်၊ ဆိုလိုသည်မှာ ၎င်းသည် ပုံမှန်ဖြန့်ဖြူးမှုထက် ပါးလွှာပြီး အမြီးများပါရှိသည်။
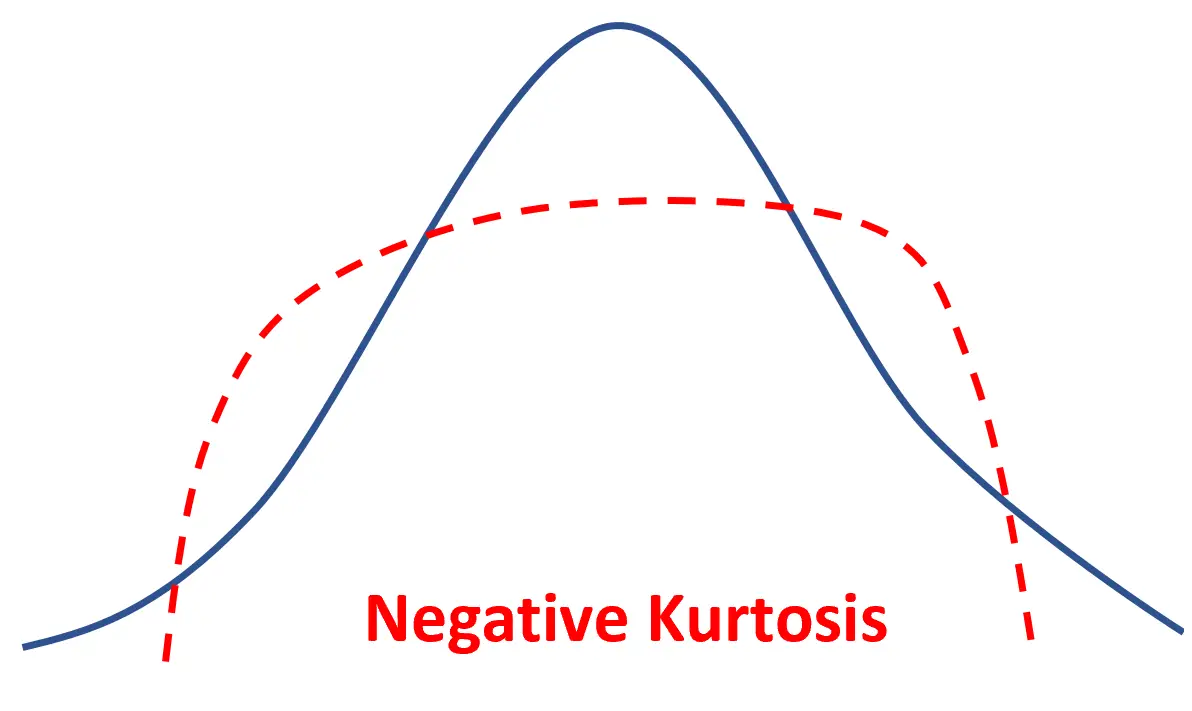
ဆိုလိုသည်မှာ ပိုမိုသောဒေတာတန်ဖိုးများသည် ဆိုလိုရင်းအနီးတွင် တည်ရှိပြီး ဒေတာတန်ဖိုးအနည်းငယ်သည် အမြီးပေါ်တွင် တည်ရှိသည်ဟု ဆိုလိုသည်။
အနုတ်လက္ခဏာ kurtosis ကိုပြသသည့် ဖြန့်ဖြူးမှု၏ လွန်ကဲသော ဥပမာမှာ အထွတ်အထိပ်မရှိသော ဖြန့် ကျက်မှုဖြစ်ပြီး တူညီသော ဖြန့်ဝေမှုဖြစ်သည်။
ဘယ်အချိန်မှာ ချော့မော့ပြီး လက်တွေ့အသုံးချရမလဲ
လက်တွေ့တွင်၊ ကျွန်ုပ်တို့သည် ဒေတာကို ပိုမိုနားလည်ရန် ရိုးရိုးရှင်းရှင်းကြိုးစားနေသောအခါတွင် ကျွန်ုပ်တို့သည် ခွဲခြမ်းစိတ်ဖြာမှုအဆင့်တွင် ဖြန့်ဖြူးမှုတစ်ခု၏ kurtosis ကို တိုင်းတာလေ့ရှိသည်။
ထို့ကြောင့် kurtosis သည် အပြုသဘောဆောင်သည်ဟု ကျွန်ုပ်တို့မြင်ပါက၊ ကျွန်ုပ်တို့သည် အလယ်ဗဟိုအနီးတွင်ရှိသော ဒေတာတန်ဖိုးများနည်းပြီး အမြီးတစ်လျှောက်တွင် ဒေတာတန်ဖိုးများ ပိုမိုဖြန့်ဝေသည့်ဖြန့်ဖြူးမှုတစ်ခုဖြင့် ကျွန်ုပ်တို့လုပ်ဆောင်နေကြောင်း ကျွန်ုပ်တို့သိပါသည်။
အပြန်အလှန်အားဖြင့်၊ ကျွန်ုပ်တို့သည် kurtosis အနုတ်လက္ခဏာကိုတွေ့မြင်ပါက၊ ကျွန်ုပ်တို့သည် စင်တာအနီးတွင်ရှိသော ဒေတာတန်ဖိုးများနှင့် အမြီးများတွင် ဒေတာတန်ဖိုးများနည်းသော ဒေတာတန်ဖိုးများပိုရှိသော ဖြန့်ဖြူးမှုတစ်ခုဖြင့် လုပ်ဆောင်နေကြောင်း ကျွန်ုပ်တို့သိပါသည်။
ထပ်လောင်းအရင်းအမြစ်များ
ပေးထားသော ဖြန့်ဖြူးမှု၏ လွဲမှားမှုနှင့် kurtosis ကိုရှာဖွေရန်၊ ဖြန့်ဖြူးမှု၏ skewness နှင့် kurtosis နှစ်ခုလုံးကို ပြောပြမည့် ဤ skewness နှင့် kurtosis ဂဏန်းတွက်စက် တွင် ဒေတာအကြမ်းထည်တန်ဖိုးများကို သင်ထည့်နိုင်သည် ။
သီးခြားဖြန့်ဖြူးမှုတစ်ခုသည် ပုံမှန်ဖြန့်ဖြူးမှုတစ်ခုနှင့် သက်ဆိုင်သည့် skewness နှင့် kurtosis ရှိကြောင်း ဆုံးဖြတ်ရန်အသုံးပြုသည့် ရေပန်းအစားဆုံး ကိန်းဂဏန်းစမ်းသပ်မှုတစ်ခုမှာ Jarque Bera test ဖြစ်သည်။
Khan Academy တွင် ဖြန့် ဖြူးပုံသဏ္ဍာန်များကို အမျိုးအစားခွဲပုံဖော်ပြသည့် ကောင်းမွန်သောစီးရီးများလည်း ရှိပါသည်။