ပဒေသာပင်

ဤဆောင်းပါးသည် စာရင်းဇယားများတွင် မျိုးရိုးလိုက်ခြင်းဟူသည်ကို ရှင်းပြထားသည်။ ထို့အပြင်၊ မျိုးကွဲရောဂါဖြစ်ပွားရခြင်းအကြောင်း၊ ၎င်း၏အကျိုးဆက်များကား အဘယ်နည်း၊ မည်သို့ပြင်ဆင်ရမည်ကို သိရှိနိုင်မည်ဖြစ်သည်။

မျိုးရိုးလိုက်ခြင်းဟူသည် အဘယ်နည်း။

စာရင်းဇယားများတွင်၊ heteroskedasticity သည် အမှားကွဲလွဲမှု မတည်မြဲဟု ဆိုလိုသော ဆုတ်ယုတ်မှုပုံစံကို တင်ပြသည့် ဝိသေသတစ်ခုဖြစ်သည်။ တစ်နည်းဆိုရသော်၊ heteroscedastic မော်ဒယ်သည် ၎င်း၏ အမှားအယွင်းများ မမှန်မကန်ကွဲလွဲမှုရှိသည်ကို ဆိုလိုသည်၊ ထို့နောက် မော်ဒယ်ကို heteroskedastic ဟုခေါ်သည်။

အမှား (သို့မဟုတ် ကျန်ရှိသော) ကို အစစ်အမှန်တန်ဖိုးနှင့် ဆုတ်ယုတ်မှုပုံစံဖြင့် ခန့်မှန်းထားသော တန်ဖိုးအကြား ကွာခြားချက်အဖြစ် သတ်မှတ်ကြောင်း သတိရပါ။

ဆုတ်ယုတ်မှုပုံစံတစ်ခုကို တည်ဆောက်သောအခါ၊ ရှုထောင့်တစ်ခုစီမှပြုလုပ်သော အမှားကို ယခင်ဖော်ပြချက်ကို အသုံးပြု၍ တွက်ချက်သည်။ ထို့ကြောင့်၊ တွက်ချက်ထားသော အမှားများ၏ ကွဲလွဲမှုသည် လေ့လာတွေ့ရှိမှုတစ်လျှောက်လုံး မတည်မြဲဘဲ ကွဲပြားသောအခါတွင် ကိန်းဂဏန်းစံနမူနာသည် ကွဲပြားပါသည်။

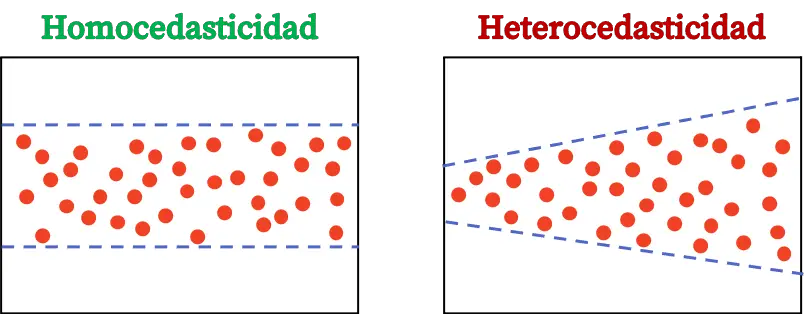
၎င်းသည် အလွန်ရိုးရှင်းသည်ဟု ထင်ရသော်လည်း၊ ဆုတ်ယုတ်မှုပုံစံသည် ကွဲပြားမှုများ မဖြစ်ပေါ်ရန် အရေးကြီးသည်၊ အဘယ်ကြောင့်ဆိုသော် မော်ဒယ်၏တွက်ချက်မှုသည် အကြွင်းအကျန်များ၏ ကွဲလွဲမှုမှာ ကိန်းသေဖြစ်သည်ဟူသောအချက်အပေါ် အခြေခံထားသောကြောင့်၊ တကယ်တော့ ၎င်းသည် ယခင်ယူဆချက်တစ်ခုဖြစ်သည်။ ဆုတ်ယုတ်မှုပုံစံများ။

White test သို့မဟုတ် Goldfeld-Quandt test ကဲ့သို့ heteroskedasticity ကို သိရှိနိုင်သော အချို့သော ကိန်းဂဏန်းစစ်ဆေးမှုများ ရှိပါသည်။ သို့သော် အများအားဖြင့် ကျန်အကြွင်းအကျန်များကို ဂရပ်ဖစ်ဖြင့် တွက်ချက်ခြင်းဖြင့် ၎င်းတို့၏ ကွဲပြားမှုကို ဖော်ထုတ်နိုင်သည်။

မျိုးကွဲခြင်း၏အကြောင်းရင်းများ

မော်ဒယ်တစ်ခုတွင် heteroskedasticity ၏အဖြစ်အများဆုံးအကြောင်းရင်းများမှာ-

• ဒေတာအကွာအဝေးသည် ပျမ်းမျှထက်စာလျှင် အလွန်ကျယ်ပြန့်သည်။ တူညီသော ကိန်းဂဏန်းနမူနာတွင် အလွန်ကြီးမားသော တန်ဖိုးများနှင့် အလွန်သေးငယ်သော တန်ဖိုးများရှိနေပါက၊ ရရှိသော ဆုတ်ယုတ်မှုပုံစံသည် ကွဲပြားသွားဖွယ်ရှိသည်။
• ဆုတ်ယုတ်မှုပုံစံရှိ ကိန်းရှင်များကို ချန်လှပ်ခြင်းသည်လည်း heteroskedasticity ကို ဖြစ်စေသည်။ ယုတ္တိနည်းအားဖြင့်၊ သက်ဆိုင်ရာ ကိန်းရှင်သည် မော်ဒယ်တွင် မပါဝင်ပါက၊ ၎င်း၏ ကွဲလွဲမှုကို ကျန်ရှိသော များတွင် ထည့်သွင်းမည်ဖြစ်ပြီး ၎င်းကို သေချာပေါက် ပြုပြင်မည်မဟုတ်ပါ။
• အလားတူ၊ ဖွဲ့စည်းပုံပြောင်းလဲမှုသည် ဒေတာအစုံနှင့် မော်ဒယ်၏ အံဝင်ခွင်ကျဖြစ်နိုင်ချေရှိပြီး ကျန်ရှိသော ကွဲလွဲမှုမှာ မတည်မြဲနိုင်ပါ။
• အချို့သော ကိန်းရှင်များသည် အခြားရှင်းပြကိန်းရှင်များထက် ပိုကြီးသောတန်ဖိုးများ ရှိသောအခါ၊ မော်ဒယ်တွင် ကွဲပြားမှုများရှိနိုင်သည်။ ဤကိစ္စတွင်၊ ပြဿနာကိုဖြေရှင်းရန် variable များကို relativized လုပ်နိုင်သည်။

သို့သော်၊ အချို့သောကိစ္စများသည် သဘာဝအားဖြင့် မျိုးရိုးဗီဇကွဲပြားမှုကို ပြသနိုင်ဖွယ်ရှိသည်။ ဥပမာအားဖြင့်၊ လူတစ်ဦး၏ ဝင်ငွေကို ၎င်းတို့၏ စားနပ်ရိက္ခာအသုံးစရိတ်ဖြင့် စံနမူနာပြုပါက၊ ချမ်းသာသောသူများသည် ဆင်းရဲသူများထက် ၎င်းတို့၏ စားနပ်ရိက္ခာအသုံးစရိတ်တွင် များစွာကွာခြားမှုရှိသည်။ အဘယ်ကြောင့်ဆိုသော် ချမ်းသာသူတစ်ဦးသည် စျေးပေါသော စားသောက်ဆိုင်များတွင် အမြဲစားလေ့ရှိသော ဆင်းရဲသူနှင့်မတူဘဲ ဈေးပေါသော စားသောက်ဆိုင်များတွင် တစ်ခါတစ်ရံ စားလေ့ရှိသောကြောင့် ဖြစ်သည်။ ထို့ကြောင့်၊ regression model အတွက် heteroskedasticity ကို ပိုင်ဆိုင်ရန် လွယ်ကူသည်။

မျိုးကွဲခြင်း၏အကျိုးဆက်များ

အဓိကအားဖြင့်၊ ဆုတ်ယုတ်မှုပုံစံတစ်ခုရှိ heteroskedasticity ၏အကျိုးဆက်များမှာ အောက်ပါအတိုင်းဖြစ်သည်။

• အမှားအယွင်းများ၏ လေးထပ်၏ ဆိုလိုရင်းအဖြစ် သတ်မှတ်ထားသော အနည်းဆုံး စတုရန်းတွက်ချက်မှုတွင် စွမ်းဆောင်ရည် ဆုံးရှုံးသွားပါသည်။
• အနဲဆုံး စတုရန်းခန့်မှန်းတွက်ချက်သူများ၏ ကာဗာရီယံမက်ထရစ် ကို တွက်ချက်ရာတွင် အမှားအယွင်းများ ဖြစ်ပေါ်ပါသည်။

ဧကကွဲအမှန်

ထွက်ပေါ်လာသော ဆုတ်ယုတ်မှုပုံစံသည် ကွဲပြားသောအခါတွင်၊

• အမှီအခိုကင်းသော ကိန်းရှင်၏ သဘာဝ လော့ဂရစ်သမ်ကို တွက်ချက်ပါ၊ အကြွင်းအကျန်များ၏ ကွဲလွဲမှုသည် ဂရပ်တွင် တိုးလာသောအခါ ယေဘုယျအားဖြင့် အသုံးဝင်သည်။
• ကျန်ရှိသောကွက်ကွက်ပေါ်မူတည်၍ သီးခြားပြောင်းလွဲပြောင်းခြင်း၏ အခြားပုံစံပြောင်းလဲခြင်းသည် ပို၍လက်တွေ့ကျပေမည်။ ဥပမာအားဖြင့်၊ ဂရပ်သည် parabola ပုံသဏ္ဍာန်ဖြစ်နေပါက၊ အမှီအခိုကင်းသော variable ၏စတုရန်းကို တွက်ချက်နိုင်ပြီး ထိုကိန်းရှင်ကို မော်ဒယ်သို့ထည့်နိုင်သည်။
• မော်ဒယ်အတွက် အခြားသော ကိန်းရှင်များကိုလည်း အသုံးပြုနိုင်သည်။ ကိန်းရှင်တစ်ခုကို ဖယ်ရှားခြင်း သို့မဟုတ် ပေါင်းထည့်ခြင်းဖြင့်၊ အကြွင်းအကျန်များ၏ ကွဲလွဲမှုကို ပြင်ဆင်နိုင်သည်။
• အနည်းဆုံး စတုရန်းစံသတ်မှတ်ချက်ကို အသုံးပြုမည့်အစား၊ အလေးချိန်အနည်းဆုံး စတုရန်းစံနှုန်းကို အသုံးပြုနိုင်သည်။

မျိုးကွဲကွဲပြားမှုနှင့် လိင်တူဆက်ဆံမှု

နောက်ဆုံးတွင်၊ ဤအရာများသည် ဆုတ်ယုတ်မှုပုံစံများ၏ သဘောတရားနှစ်ရပ်ဖြစ်သောကြောင့် ကျွန်ုပ်တို့ရှင်းရှင်းလင်းလင်းသိထားရမည့်အချက်များဖြစ်သောကြောင့် စာရင်းဇယားများတွင် မျိုးရိုးလိုက်ခြင်း နှင့် မျိုးရိုးဗီဇကွဲပြားခြင်းအကြား ခြားနားချက်များကို ကျွန်ုပ်တို့တွေ့ရပါမည်။

ဆုတ်ယုတ်မှုပုံစံတစ်ခု၏ တူညီသောအချိုးအစား သည် အမှားကွဲလွဲမှုမှာ ကိန်းသေဖြစ်ကြောင်း ညွှန်ပြသည့် ကိန်းဂဏန်းလက္ခဏာတစ်ခုဖြစ်သည်။ ထို့ကြောင့်၊ homoscedastic မော်ဒယ်သည် ၎င်း၏အမှားအယွင်းများ၏ကွဲလွဲမှုသည် စဉ်ဆက်မပြတ်ဖြစ်ကြောင်း ဆိုလိုသည်။

အကြွင်းအကျန်များ၏ ကွဲလွဲမှု၏ အဆက်မပြတ်တည်ရှိမှု နှင့် မျိုးကွဲကွဲပြားခြင်း အကြား ခြားနားချက်ကို တွေ့ရှိရသည်။ မော်ဒယ်၏ အကြွင်းအကျန်များ၏ ကွဲလွဲမှုသည် မတည်မြဲပါက၊ မော်ဒယ်သည် ကွဲလွဲနေသည်ဟု ဆိုလိုသည်။ အခြားတစ်ဖက်တွင်၊ အကြွင်းအကျန်များ၏ကွဲလွဲမှုသည် စဉ်ဆက်မပြတ်ဖြစ်နေပါက ၎င်းသည် homoscedastic ဖြစ်သည်ဟုဆိုလိုသည်။

ထို့ကြောင့်၊ ကျွန်ုပ်တို့တည်ဆောက်သော ဆုတ်ယုတ်မှုပုံစံသည် တူညီကြောင်း သေချာစေရန် လိုအပ်သည်၊ ဤနည်းဖြင့် ကျန်အကြွင်းအကျန်များ၏ ကွဲလွဲမှုမှာ ကိန်းသေဖြစ်တည်မှုကို ဖြည့်ဆည်းပေးမည်ဖြစ်သည်။