Confidence ကြားကာလအတွက် ခြားနားချက်ကို ဆိုလိုသည်။
ဤဆောင်းပါးတွင် စာရင်းအင်းဆိုင်ရာ အဓိပ္ပါယ်ဖွင့်ဆိုချက်များ ခြားနားချက်အတွက် ယုံကြည်မှုကြားကာလနှင့် ၎င်းကို မည်သည့်အရာအတွက် အသုံးပြုကြောင်း ရှင်းပြထားသည်။ ထို့ကြောင့်၊ နည်းလမ်းနှစ်ခု၏ခြားနားချက်အတွက် ယုံကြည်မှုကြားကာလကို တွက်ချက်နည်းနှင့် လေ့ကျင့်ခန်းတစ်ခုကို တစ်ဆင့်ပြီးတစ်ဆင့် ဖြေရှင်းနိုင်မည်ဖြစ်သည်။
ဆိုလိုသည်မှာ ခြားနားချက်အတွက် ယုံကြည်မှုကြားကာလသည် အဘယ်နည်း။
နည်းလမ်းများ၏ ခြားနားမှုအတွက် ယုံကြည်မှုကြားကာလ သည် အမြင့်ဆုံးတန်ဖိုးနှင့် အနိမ့်ဆုံးတန်ဖိုးကို ပေးဆောင်သည့် ကြားကာလတစ်ခုဖြစ်ပြီး လူဦးရေနှစ်ခု၏ ကွာခြားချက်တန်ဖိုးသည် ယုံကြည်စိတ်ချမှုအဆင့်တစ်ခုဖြင့် တည်ရှိနေပါသည်။
ဥပမာအားဖြင့်၊ လူဦးရေ 95% ယုံကြည်မှုအဆင့်ရှိ လူဦးရေနှစ်ခု၏ ခြားနားချက်အတွက် ယုံကြည်မှုကြားကာလသည် (3.5) ဖြစ်ပါက၊ ဆိုလိုသည်မှာ လူဦးရေနှစ်ခု၏ ကွာခြားချက်မှာ 3 နှင့် 5 ကြားဖြစ်နိုင်ခြေ 95 ဖြစ်လိမ့်မည်၊ %
ထို့ကြောင့် ကိန်းဂဏန်းစာရင်းဇယားများတွင် ယုံကြည်စိတ်ချမှုကြားကာလကို ဆိုလိုသည်မှာ လူဦးရေနှစ်ခုကြား ခြားနားချက်သည် မုသာစကားများကြားတွင် တန်ဖိုးနှစ်ခုကို ခန့်မှန်းရန် အသုံးပြုသည်။ ထို့ကြောင့် နမူနာနှစ်ခုမှ ဒေတာကို အသုံးပြု၍ လူဦးရေ၏ ကွာခြားချက်ကို အနီးစပ်ဆုံး ခန့်မှန်းရန် ဖြစ်နိုင်သည်။
Confidence interval formula for ခြားနားချက်ကို ဆိုလိုသည်။
အဓိပ္ပါယ် ကွာခြားချက်အတွက် ယုံကြည်မှုကြားကာလအတွက် ဖော်မြူလာသည် လူဦးရေကွဲလွဲမှုများကို သိနိုင်သည်ဖြစ်စေ မကွဲပြားခြင်းအပေါ် မူတည်ပြီး လူဦးရေကွဲလွဲမှု တူညီနိုင်သည်ဖြစ်စေ မဟုတျပါ။ . ထို့နောက် အမှုတစ်ခုစီတွင် ခြားနားချက်အတွက် ယုံကြည်ချက်ကြားကာလကို မည်သို့ တွက်ချက်သည်ကို ကြည့်ပါမည်။
သွေဖီခြင်းများကို သိရှိသည်။
1-α ယုံကြည်မှုအဆင့် ဖြင့် လူဦးရေနှစ်ခု၏ကွဲလွဲမှုများကို သိရှိသောအခါ ခြားနားချက်အတွက် ယုံကြည်မှုကြားကာလကို တွက်ချက်ရန် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်-
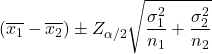
ရွှေ-
-

နမူနာ i ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
-

လူဦးရေ၏စံသွေဖည်မှု i။
-

ဖြစ်နိုင်ခြေ α/2 ရှိသော စံပုံမှန် ဖြန့်ဖြူးမှု၏ တန်ဖိုးဖြစ်သည်။
-

နမူနာအရွယ်အစား i ဖြစ်ပါတယ်။
လူဦးရေကွဲပြားမှု၏တန်ဖိုးကို ယေဘူယျအားဖြင့် မသိသောကြောင့် ဤကိစ္စသည် အဖြစ်နည်းဆုံးဖြစ်သည်။
အမည်မသိနှင့် တန်းတူကွဲလွဲမှုများ
လူဦးရေ နှစ်ခု၏ ကွဲလွဲမှုကို မသိရသော်လည်း တူညီသည်ဟု ခန့်မှန်းနိုင်သောအခါ၊ ယုံကြည်မှုအဆင့် 1-α ၏ ခြားနားချက်အတွက် ယုံကြည်ချက်ကြားကာလကို တွက်ချက်သည့် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်-
![]()
ရွှေ-
-

နမူနာ i ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
-

စံသွေဖည်မှု ပေါင်းစည်းသည်။
-

α/2 ဖြစ်နိုင်ခြေရှိသော လွတ်လပ်မှု၏ n 1 + n 2 -2 ဒီဂရီ၏ ကျောင်းသား၏ t ဖြန့်ဖြူးမှုတန်ဖိုးဖြစ်သည်။
-

နမူနာအရွယ်အစား i ဖြစ်ပါတယ်။
ဤအခြေအနေတွင် လူဦးရေကွဲလွဲမှုများသည် ညီမျှသည်ဟု ယူဆသောကြောင့်၊ ယုံကြည်မှုကြားကာလကို တွက်ချက်ရန်အတွက် ပေါင်းစပ်စံသွေဖည်မှုကို အသုံးပြုပြီး၊ အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်သည်-

ရွှေ
![]()
နမူနာ i ၏ စံသွေဖည်သည်။
အမည်မသိနှင့် မတူညီသော ကွဲပြားမှုများ
လူဦးရေ နှစ်ခု၏ ကွဲလွဲမှုများကို မသိ၍ တူညီသည်ဟု မယူဆနိုင်သောအခါ၊ ယုံကြည်မှုအဆင့် 1-α ၏ ခြားနားချက်ကို တွက်ချက်ရန်အတွက် ဖော်မြူလာမှာ အောက်ပါအတိုင်း ဖြစ်သည်။
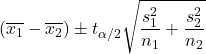
ရွှေ-
-

နမူနာ i ၏ ဆိုလိုရင်းဖြစ်ပါသည်။
-
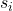
နမူနာ i ၏ စံသွေဖည်သည်။
-

ဖြစ်နိုင်ခြေရှိသော α/2 ရှိသော ကျောင်းသား၏ t ဖြန့်ဖြူးမှုတန်ဖိုးဖြစ်သည်။
-

နမူနာအရွယ်အစား i ဖြစ်ပါတယ်။
ဤကိစ္စတွင်၊ ကျောင်းသား၏ t ဖြန့်ဝေမှု၏ လွတ်လပ်မှုဒီဂရီကို အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်သည်-

ရွှေ
![]()
နမူနာ i ၏ စံသွေဖည်သည်။
ယုံကြည်မှုကြားကာလ၏ ခိုင်မာသော ဥပမာကိုဆိုလိုသည်။
အဓိပ္ပါယ်အမျိုးမျိုးအတွက် ယုံကြည်မှုကြားကာလ၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်အား မြင်တွေ့ပြီးနောက်၊ နည်းလမ်းနှစ်ခု၏ ခြားနားချက်အတွက် ယုံကြည်မှုကြားကာလကို မည်ကဲ့သို့ တွက်ချက်မည်ကို ပေါင်းစည်းရန် ခိုင်မာသော ဥပမာတစ်ခုကို ကျွန်ုပ်တို့ ယခုတွေ့မြင်ရမည်ဖြစ်ပါသည်။
- ကလေးများ၏ မွေးရာပါကိုယ်အလေးချိန်အပေါ် ဆေးလိပ်၏အကျိုးသက်ရောက်မှုကို လေ့လာလိုပါသည်။ ယင်းကိုလုပ်ဆောင်ရန် နမူနာနှစ်ခုကို နှိုင်းယှဉ်ကြည့်သည်- ပထမနမူနာတွင် မိခင် ဆေးလိပ်မသောက်သော ကလေးများနှင့် ဒုတိယနမူနာတွင် မိခင် ဆေးလိပ်သောက်သော ကလေးများ ပါဝင်သည် (နမူနာဘောင်များကို အောက်တွင်ဖော်ပြထားသည်)။ ယုံကြည်မှုအဆင့် 95% ဖြင့် ဆိုလိုသည်မှာ ခြားနားချက်အတွက် ယုံကြည်မှုကြားကာလကို တွက်ချက်ပါ။
- ဆေးလိပ်မသောက်သောမိခင်များ
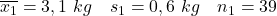
- ဆေးလိပ်သောက်မိခင်များ
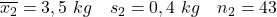
- ဆေးလိပ်မသောက်သောမိခင်များ
ဤအခြေအနေတွင် ကျွန်ုပ်တို့သည် လူဦးရေကွဲလွဲမှု၏တန်ဖိုးများကို မသိရသော်လည်း၊ ကျွန်ုပ်တို့သည် အလွန်တူညီသောလက္ခဏာများရှိသော လူဦးရေနှစ်မျိုးနှင့် ဆက်ဆံနေရသောကြောင့် လူဦးရေကွဲလွဲမှုများသည် ညီမျှသည်ဟု ကျွန်ုပ်တို့ယူဆနိုင်သည်။ ထို့ကြောင့်၊ ခြားနားချက်အတွက် ယုံကြည်မှုကြားကာလအတွက် ဖော်မြူလာကို ကျွန်ုပ်တို့အသုံးပြုသင့်သည်-
![]()
ထို့ကြောင့် ကျွန်ုပ်တို့သည် နမူနာနှစ်ခု၏ စံသွေဖည်မှုများမှ ပေါင်းစပ်စံသွေဖည်မှုကို တွက်ချက်သည်-
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(39-1)\cdot 0,6^2+(43-1)\cdot 0,4^2}{39+43-2}}\\[2ex]\displaystyle s_p&=0,50\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-688958252e9838e7fddc2ddcb9061b01_l3.png)
အလားတူ၊ ကျောင်းသား၏ t ဖြန့်ဖြူးမှု၏ ဖြစ်နိုင်ခြေ ဖြန့်ချီမှုဇယားတွင် ဖြစ်နိုင်ခြေ 2.5% ရှိသည့် လွတ်လပ်မှု 80 ဒီဂရီ၏ ကျောင်းသား၏ t ဖြန့်ဖြူးမှုတန်ဖိုးကို ကျွန်ုပ်တို့ ရှာဖွေရမည်ဖြစ်ပါသည်။
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025|80}=1,990\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5e4ea90fdc33c9a3d3dab0f1d9d29af0_l3.png)
နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် နည်းလမ်းများ၏ ခြားနားချက်အတွက် ဒေတာကို ယုံကြည်မှုကြားကာလဖော်မြူလာအဖြစ် အစားထိုးပြီး တွက်ချက်မှုများကို လုပ်ဆောင်သည်-
![]()
![]()
![]()
ထို့ကြောင့် ပြဿနာ၏နည်းလမ်းများ၏ ခြားနားချက်အတွက် ယုံကြည်မှုကြားကာလမှာ အောက်ပါအတိုင်းဖြစ်သည်။
![]()