Stata တွင် ရိုးရှင်းသော မျဉ်းကြောင်းပြန်ဆုတ်ခြင်းကို မည်သို့လုပ်ဆောင်ရမည်နည်း။

ရိုးရှင်းသော linear regression သည် explanatory variable, x နှင့် response variable, y တို့ကြား ဆက်နွယ်မှုကို နားလည်ရန် သင်အသုံးပြုသည့် နည်းလမ်းတစ်ခုဖြစ်သည်။

ဤသင်ခန်းစာသည် Stata တွင် ရိုးရိုးမျဉ်းကြောင်းပြန်ဆုတ်ခြင်းကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။

ဥပမာ- Stata ရှိ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှု

ကားတစ်စီး၏အလေးချိန်နှင့် ၎င်း၏တစ်ဂါလံမိုင်အကြား ဆက်နွယ်မှုကို ကျွန်ုပ်တို့ နားလည်လိုသည်ဆိုပါစို့။ ဤဆက်နွယ်မှုကို စူးစမ်းလေ့လာရန်၊ တုံ့ပြန်မှုကိန်းရှင်အဖြစ် အလေးချိန်ကို ရှင်းပြနိုင်သောကိန်းရှင်နှင့် တုံ့ပြန်မှုကိန်းရှင်အဖြစ် ဂါလံတစ်မိုင်ကို အသုံးပြု၍ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုကို လုပ်ဆောင်နိုင်သည်။

မတူညီသောကား 74 စီးတွင် ဒေတာပါရှိသော auto ဟုခေါ်သော ဒေတာအတွဲကို အသုံးပြု၍ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုလုပ်ဆောင်ရန် Stata တွင် အောက်ပါအဆင့်များကို ပြီးအောင်လုပ်ပါ။

အဆင့် 1: ဒေတာကို တင်ပါ။

command box တွင် အောက်ပါတို့ကို ရိုက်ထည့်ခြင်းဖြင့် ဒေတာကို တင်ပါ-

https://www.stata-press.com/data/r13/auto ကို အသုံးပြုပါ။

အဆင့် 2- ဒေတာအကျဉ်းချုပ်ကို ရယူပါ။

Command box တွင် အောက်ပါတို့ကို ရိုက်ထည့်ခြင်းဖြင့် သင်လုပ်ဆောင်နေသော ဒေတာကို လျင်မြန်စွာ နားလည်နိုင်သည်-

အကျဉ်းချုပ်ရန်

dataset တွင် မတူညီသော variable 12 ခုရှိသည်ကိုကျွန်ုပ်တို့တွေ့မြင်နိုင်သော်လည်းကျွန်ုပ်တို့အလေးထားသောနှစ်ခုမှာ mpg နှင့် weight ဖြစ်သည်။

အဆင့် 3: ဒေတာကိုမြင်ယောင်ကြည့်ပါ။

ရိုးရှင်းသော linear regression ကိုမလုပ်ဆောင်မီ၊ ပထမဦးစွာ mpg နှင့် အလေးချိန်၏ခွဲခြမ်းစိပ်ဖြာမှုတစ်ခုကို ဖန်တီးကြပါစို့၊ သို့မှသာ ဤကိန်းရှင်နှစ်ခုကြားရှိ ဆက်စပ်မှုကို မြင်သာစေပြီး ထင်ရှားသောအကွာအဝေးများကို စစ်ဆေးကြည့်ကြပါစို့။ scatterplot ဖန်တီးရန် Command box တွင် အောက်ပါတို့ကို ရိုက်ထည့်ပါ။

စိုင်းစိုင်းခမ်းလှိုင် အလေးချိန် ပျံ့လွင့်မှု

၎င်းသည် အောက်ဖော်ပြပါ ဖြန့်ကျက်ကွက်ကို ထုတ်ပေးသည်-

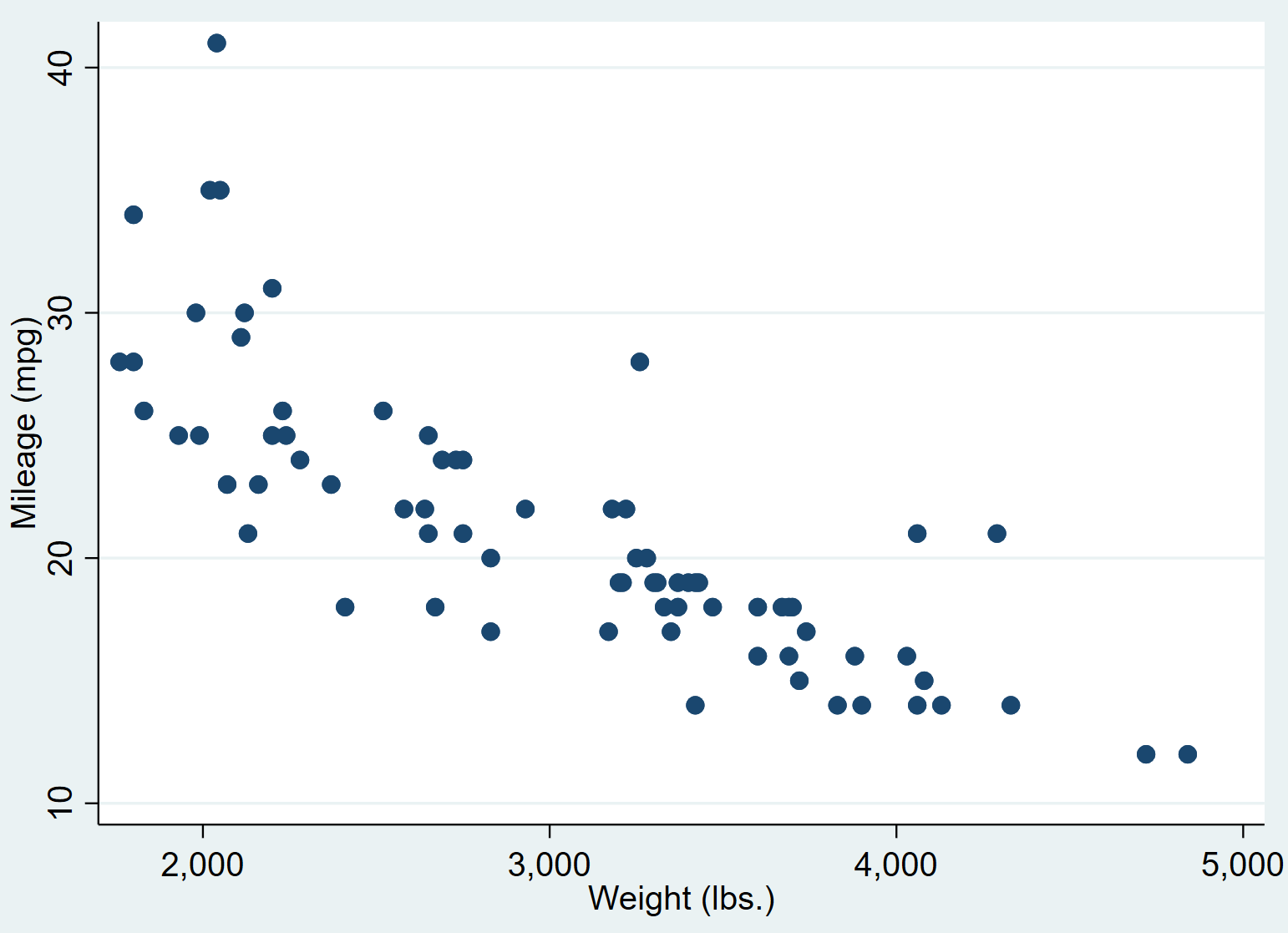
အလေးချိန်ပိုမြင့်သော ကားများသည် တစ်ဂါလံလျှင် မိုင်အနည်းငယ်သာ ရှိသည်ကို ကျွန်ုပ်တို့ တွေ့နိုင်သည်။ ဤဆက်နွယ်မှုကို တွက်ချက်ရန်အတွက်၊ ယခု ကျွန်ုပ်တို့သည် ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုကို လုပ်ဆောင်ပါမည်။

အဆင့် 4- ရိုးရှင်းသော မျဉ်းကြောင်းပြန်ဆုတ်ခြင်းကို လုပ်ဆောင်ပါ။

ရှင်းလင်းချက်ကိန်းရှင်အဖြစ် အလေးချိန်နှင့် တုံ့ပြန်မှုကိန်းရှင်အဖြစ် mpg ကို အသုံးပြု၍ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုလုပ်ဆောင်ရန် အောက်ပါတို့ကို Command box တွင် ရိုက်ထည့်ပါ။

အလေးချိန်ကို စိုင်းစိုင်းခမ်းလှိုင်သို့ ပြန်ပြောင်းပါ။

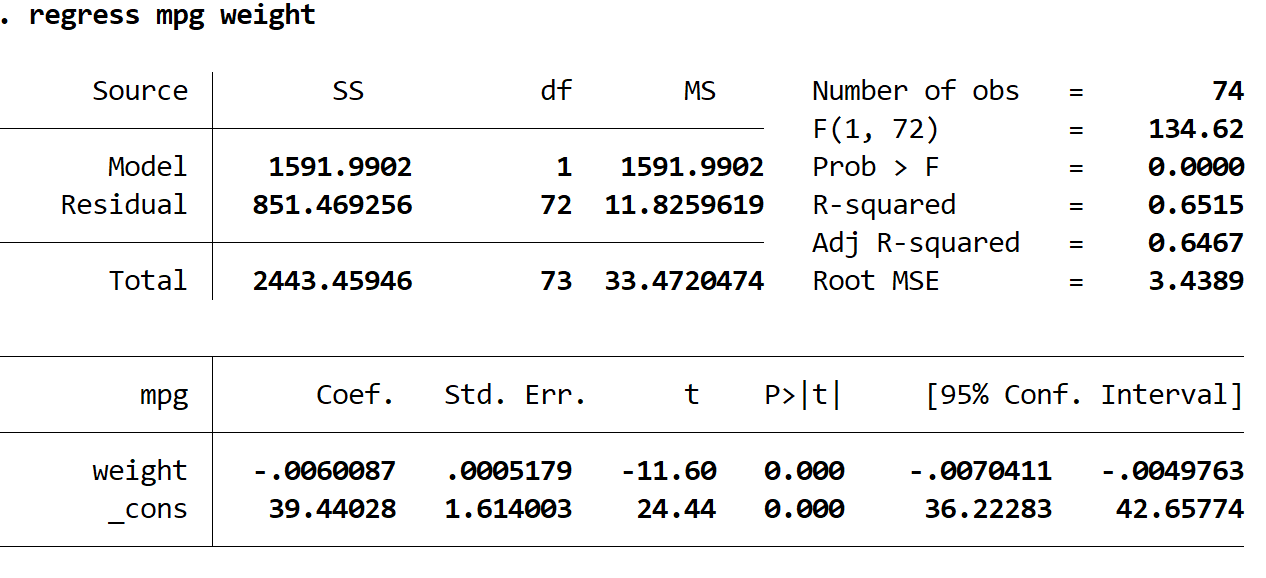
ရလဒ်တွင် စိတ်ဝင်စားစရာအကောင်းဆုံးဂဏန်းများကို အဓိပ္ပာယ်ဖွင့်ဆိုပုံမှာ အောက်ပါအတိုင်းဖြစ်သည်။

R နှစ်ထပ်ကိန်း- 0.6515။ ဤသည်မှာ explanatory variable ဖြင့် ရှင်းပြနိုင်သော တုံ့ပြန်မှုကိန်းရှင်ရှိ ကွဲလွဲမှု၏ အချိုးအစားဖြစ်သည်။ ဤဥပမာတွင်၊ စိုင်းစိုင်းခမ်းလှိုင်၏ 65.15% ကို အလေးချိန်ဖြင့် ရှင်းပြနိုင်သည်။

Coef (အလေးချိန်): -0.006။ ၎င်းသည် ရှင်းပြချက်ကိန်းရှင်တွင် တစ်ယူနစ်တိုးခြင်းနှင့် ဆက်စပ်နေသော တုံ့ပြန်မှုကိန်းရှင်၏ ပျမ်းမျှပြောင်းလဲမှုကို ကျွန်ုပ်တို့အား ပြောပြသည်။ ဤဥပမာတွင်၊ ကိုယ်အလေးချိန်တစ်ပေါင်စီတိုးခြင်းသည် ပျမ်းမျှအားဖြင့် 0.006 mpg ကျဆင်းခြင်းနှင့် ဆက်စပ်နေသည်။

Coef (_cons): 39.44028။ ၎င်းသည် ရှင်းပြချက်ကိန်းရှင် သုညဖြစ်သောအခါ တုံ့ပြန်မှုကိန်းရှင်၏ ပျမ်းမျှတန်ဖိုးကို ပြောပြသည်။ ဤဥပမာတွင်၊ ကားတစ်စီး၏အလေးချိန်သည် သုညဖြစ်သောအခါ ပျမ်းမျှ mpg သည် 39.44028 ဖြစ်သည်။ ကားတစ်စီး၏အလေးချိန်သည် သုညမဖြစ်နိုင်သောကြောင့် အဓိပ္ပါယ်ပြန်ဆိုရန် အဓိပ္ပါယ်မရှိသော်လည်း၊ နံပါတ် 39.44028 သည် regression equation ကိုဖွဲ့စည်းရန် လိုအပ်ပါသည်။

P>|t| (အလေးချိန်) : 0,000 ။ ၎င်းသည် ကိုယ်အလေးချိန်အတွက် စမ်းသပ်မှုစာရင်းအင်းနှင့် ဆက်စပ်နေသည့် p-တန်ဖိုးဖြစ်သည်။ ဤကိစ္စတွင်၊ ဤတန်ဖိုးသည် 0.05 ထက်နည်းသောကြောင့်၊ အလေးချိန်နှင့် စိုင်းစိုင်းခမ်းလှိုင်ကြားတွင် စာရင်းအင်းအရ သိသာထင်ရှားသော ဆက်နွယ်မှုရှိကြောင်း ကျွန်ုပ်တို့ ကောက်ချက်ချနိုင်သည်။

Regression equation- နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် coefficient တန်ဖိုးနှစ်ခုကို အသုံးပြု၍ regression equation ကို ဖန်တီးနိုင်သည်။ ဤကိစ္စတွင်၊ ညီမျှခြင်းမှာ-

ခန့်မှန်းထားသော စိုင်းစိုင်းခမ်းလှိုင် = 39.44028 – 0.0060087*(အလေးချိန်)

ကားတစ်စီးအတွက် မျှော်မှန်းထားသည့် စိုင်းစိုင်းခမ်းလှိုင်ကို ၎င်း၏အလေးချိန်ဖြင့် ရှာဖွေရန် ဤညီမျှခြင်းကို အသုံးပြုနိုင်သည်။ ဥပမာအားဖြင့်၊ ပေါင် 4,000 အလေးချိန်ရှိသော ကားတစ်စီးတွင် mpg 15,405 ရှိသင့်သည်-

စိုင်းစိုင်းခမ်းလှိုင် = 39.44028 – 0.0060087*(4000) = 15.405

အဆင့် 5: ရလဒ်များကို သတင်းပို့ပါ။

နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် ကျွန်ုပ်တို့၏ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှု၏ရလဒ်များကို အစီရင်ခံလိုပါသည်။ ဤသည်မှာ ဤအရာကို ပြုလုပ်ပုံ၏ ဥပမာတစ်ခုဖြစ်သည်။

ကားတစ်စီး၏အလေးချိန်နှင့် ၎င်း၏တစ်ဂါလံမိုင်အကြား ဆက်နွယ်မှုကို တွက်ချက်ရန်အတွက် linear regression ကို လုပ်ဆောင်ခဲ့သည်။ ခွဲခြမ်းစိတ်ဖြာမှုတွင် နမူနာကား ၇၄ စီးကို အသုံးပြုခဲ့သည်။

ရလဒ်များက အလေးချိန်နှင့် စိုင်းစိုင်းခမ်းလှိုင် (t=-11.60၊ p < 0.0001) အကြား ကိန်းဂဏန်းအရ သိသာထင်ရှားသော ဆက်နွယ်မှုရှိကြောင်း ပြသခဲ့ပြီး အလေးချိန်သည် စိုင်းစိုင်းခမ်းလှိုင်၏ 65.15% ရှိကြောင်း ရှင်းပြထားသည်။

ဆုတ်ယုတ်မှုညီမျှခြင်းမှာ-

စိုင်းစိုင်းခမ်းလှိုင် = 39.44 – 0.006 (အလေးချိန်)

အပိုပေါင်တစ်ခုစီသည် ပျမ်းမျှအားဖြင့် တစ်ဂါလံလျှင် -0.006 မိုင် ကျဆင်းခြင်းနှင့် ဆက်စပ်နေသည်။